【循環小数の表し方】分数にする方法などを基礎から解説するぞ！

小数って、大きく分類すると

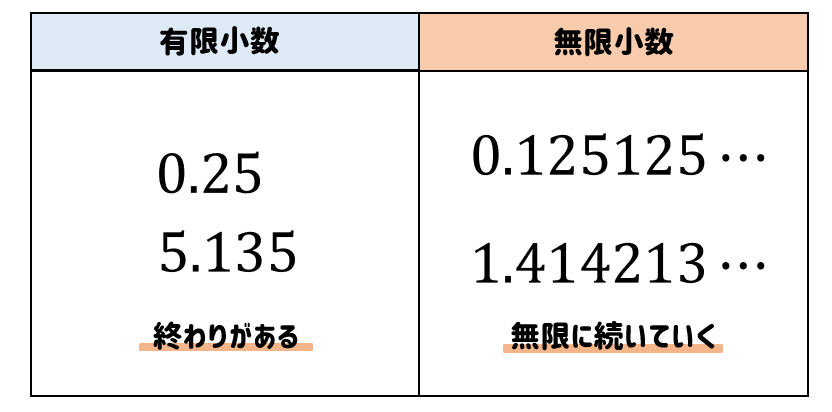
限りがある小数、つまり有限小数

無限に続いていく小数、つまり無限小数があります。

 

 

更に、無限小数の中でも

ある数が繰り返し出てくる規則的な小数を循環小数といいます。

一方で、なんの規則性もなく無限に続いていく小数には

特別な名前があるわけではなく

循環しない無限小数という呼び方があります。

 

 

今回の記事では、そんな小数の種類の中から

ある数が規則的に繰り返される循環小数について取り上げていきます。

以上の3点について、イチから解説していくぞ！

 

循環小数についてはこちらの動画でも解説しています。

循環小数の表し方

$$0.125125125125\cdots$$

んー、無限に続いていくから書くのが大変だ…

もっとラクに表現できると嬉しいんだけど…

ってことで！

循環小数に関して、ちょっと特別な表し方があります。

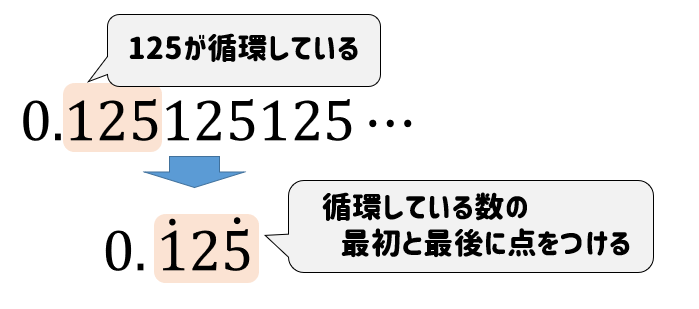
こんな感じ！簡単だね(^^)

\(125\)という数字が循環しているので

循環している数グループの最初と最後の数の上に点を書くだけ！

これで循環小数を表現することができるのです。

 

もしも、\(0.333333\cdots\) のように1つの数が循環する場合には

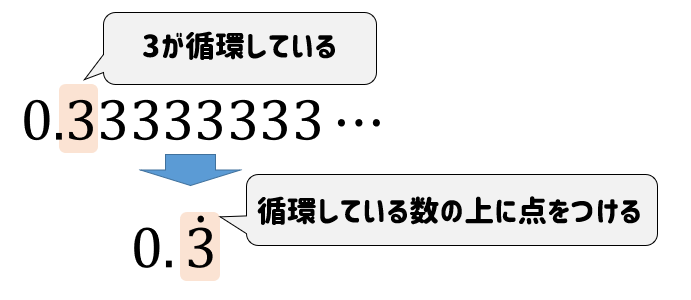
点を取るのは循環している\(3\)の上だけでOKです。

 

では、次の循環小数はどうやって表せばいいかわかるかな？

 

分数を循環小数で表す方法

では、循環小数の表し方を知ったところで

次の問題を見ていきましょう。

分数を小数で表すには、（分子）÷（分母）を計算する必要があります。

だけど、実際に計算をしていみると…

$$2\div 9=0.22222\cdots$$

循環小数になってしまいます。

そこで、出番になるのが先ほど学習した循環小数の表し方です！

循環小数の表し方を覚えてしまえば、こういった問題も楽勝になりますね(^^)

では、練習問題に挑戦してみましょう。

 

循環小数を分数にする方法

すべての循環小数は分数で表すことができます。

この章では、循環小数を分数にする方法を学んでいきましょう。

手順①　循環小数を\(x=\cdots\) とする。

まずは、これからの計算は分かりやすくするため

$$x=0.2727\cdots$$

このように表します。

 

手順②　×10、×100をして小数点の位置を循環している数の後ろまで動かす。

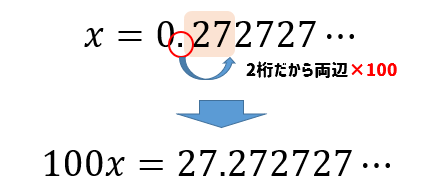
循環している27の後ろまで小数点を動かします。

今回の場合であれば、小数点を2つ動かせばよいので×100をすればOK

よって、\(100x=27.2727\cdots\) という式を作ります。

 

手順③　2つの式を引く！

\(x=0.2727\cdots\)、\(100x=27.2727\cdots\)

この2つの式を引きます。

それぞれの式は、小数点以下が同じになっているので

互いの式を引くと、小数がなくなってしまいます。

そこからは方程式を解いていくことで、\(x=\frac{3}{11}\)ということが分かります。

 

\(x\)というのは、\(0.2727\cdots\)のことですから

$$0.\dot{2}\dot{7}=\color{red}{\frac{3}{11}}$$

このように循環小数を分数で表せたことになります。

では、以上の手順を踏まえて

次の発展問題も考えてみましょう。

まずは手順①\(x=\cdots\) としましょう。

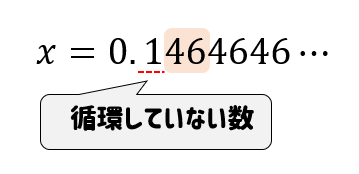
$$x=0.14646\cdots$$

次に手順②なのですが、小数点以下に1という循環しない数も含まれています。

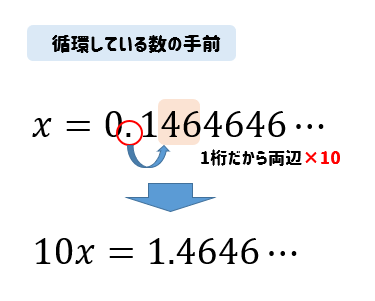
こういう場合には、次のように式を変形して2つの式を作ります。

 

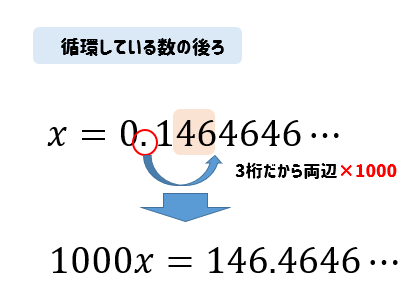
2つの式が出来上がったら手順③です。

 

よって

$$0.1\dot{4}\dot{6}=\color{red}{\frac{29}{198}}$$

となります。

ポイントは、手順②でそれぞれの式の小数点以下が同じになるように調整するってことですね！

まとめ！

お疲れさまでした(^^)

以上が、循環小数の表し方と分数にする方法でした。

式がゴチャゴチャしているように見えるので

難しく感じてしまうのですが、やっていることはすごくシンプルでしたね。

それに複雑な計算もありません(^^)

小数点を動かして、引き算するだけだ！

 

たくさん練習して、しっかりと手順を身につけておきましょう(/・ω・)/