高校で学習する因数分解は複雑で難しい！！
「わからないので教えてください」と質問をいただくことの多い単元でもあります。
なので、今回の記事では高校1年生で学習する因数分解のやり方についてパターン別にまとめておきます。
解き方の分からない因数分解に出会ったときには、この記事を解き方の辞書代わりに使ってもらえると嬉しいです(^^)
共通因数をくくる因数分解
共通因数でくくる因数分解
$$AB+AC=A(B+C)$$
共通因数についてイチから学習したい方はこちらの記事もおススメです。
⇒ 【因数分解】共通因数でくくる場合のやり方は？マイナスのときはどうする？
次の因数分解をせよ。
$$3x^2y-6xy^2$$
各項に共通因数がある場合には、くくり出すようにしましょう。
次の式を因数分解せよ。
$$(x+y)a-(x+y)b$$
共通因数というのは、単項式だけとは限りません。
このように式のかたまりを共通因数としてくくり出すこともできます。
むしろこちらの方が高校数学っぽくてよく出てきます。
次の式を因数分解せよ。
$$(x-3y)a+(3y-x)b$$
かたまりの式が共通因数になっている場合には、このようにマイナスでくくってからというものもあります。
数や文字は一緒なんだけど、符号が違うんだよな…というときにはマイナスでくくると解決しますね(^^)
次の式を因数分解せよ。
$$ax+3x-ay-3y$$
これはちょっと発展的。
くくってあげることで共通因数を見つけるというパターンですね。
練習問題（共通因数）
次の式を因数分解せよ。
$$6a^3b+2a^2b^2-2ab^3$$
次の式を因数分解せよ。
$$2a(a-5b)-b(5b-a)$$
次の式を因数分解せよ。
$$x(a-b)-ya+yb$$
公式を使った因数分解
因数分解の公式
$$a^2+2ab+b^2=(a+b)^2$$
$$a^2-2ab+b^2=(a-b)^2$$
$$a^2-b^2=(a+b)(a-b)$$
$$x^2+(a+b)x+ab=(x+a)(x+b)$$
ここの因数分解については、
中学で学習した内容がそのままなので省略！
イチから学習したい場合は詳しくはこちらの記事をご参考ください。
⇒ 【因数分解の公式】中学生の問題まとめ！それぞれのやり方は？
たすき掛けの因数分解
因数分解の公式（たすき掛け）
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
文字が入った公式だけでは理解しにくいですね。
こちらの記事では「たすき掛け」について詳しく解説をしているのでご参考ください。
⇒ 【たすき掛けの因数分解】コツを学んでやり方をマスターしよう！
次の式を因数分解せよ。
$$2x^2+9x+10$$
かけて2、10になる数の組み合わせから、たすき掛けをしたときに9になるものを見つけましょう。
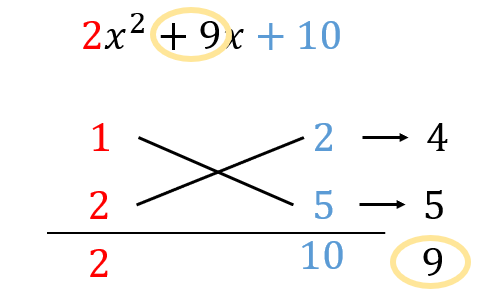
$$\begin{eqnarray}2x^2+9x+10=(x+2)(2x+5)\cdots (解) \end{eqnarray}$$
次の式を因数分解せよ。
$$6x^2+5x-6$$
定数項が\(-6\)となっているので、符号にも注意しながら組み合わせを見つけましょう。
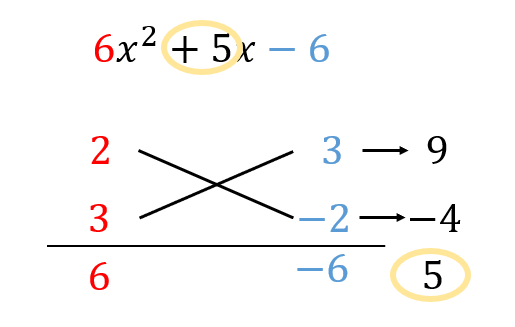
$$\begin{eqnarray}&&6x^2+5x-6\\[5pt]&=&(2x+3)(3x-2)\cdots (解) \end{eqnarray}$$
次の式を因数分解せよ。
$$6x^2+17xy+12y^2$$
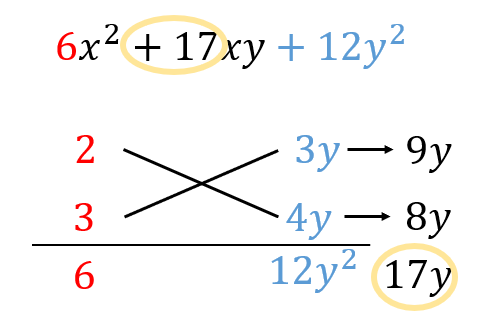
$$\begin{eqnarray}&&6x^2+17xy+12y^2\\[5pt]&=&(2x+3y)(3x+4y)\cdots (解) \end{eqnarray}$$
練習問題（たすき掛け）
次の式を因数分解せよ。
$$3x^2+7x+2$$
次の式を因数分解せよ。
$$4a^2+5a-21$$
次の式を因数分解せよ。
$$12x^2-8xy-15y^2$$
3乗の和と差の因数分解
3乗の和と差の公式
$$a^3+b^3=(a+b)(a^2-ab+b^2)$$
$$a^3-b^3=(a-b)(a^2+ab+b^2)$$
簡単な公式なので使い方を確認しておきましょう。
次の式を因数分解せよ。
$$8x^3-27$$
式を見たときに、(三乗)＋(三乗)、(三乗)－(三乗)の形になっていれば、この公式を使うことができます。
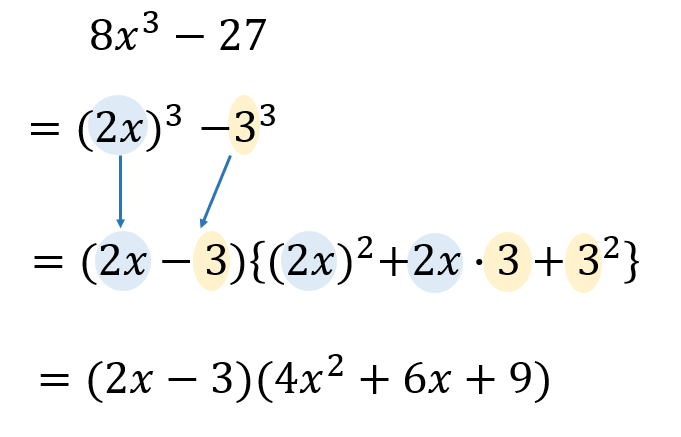
このように、公式に当てはめていくと因数分解が完成します。
まずはパッと見たときに何の3乗になっているか、判断ができるようにしておきたいですね。
よく出てくる3乗の形は以下の通りです。これらは頭に入れておきましょう。
$$8=2^3$$
$$27=3^3$$
$$64=4^3$$
$$125=5^3$$
$$216=6^3$$
練習問題（3乗の和と差）
次の式を因数分解せよ。
$$x^3+27$$
次の式を因数分解せよ。
$$125a^3-b^3$$
次の式を因数分解せよ。
$$64x^3-125y^3$$
【発展】置き換えによる因数分解
まとまった式や同じ式は置き換えを利用して、簡単な形に変えてやりましょう。
次の式を因数分解せよ。
$$(x+y)^2+6(x+y)+5$$
2乗があるからといって、展開してはダメ！
展開すると余計にややこしくなってしまいます(^^;)
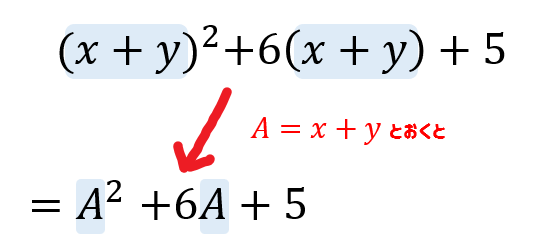
このように同じ部分を置き換えることで、因数分解しやすい形になります。
最後に置き換えをもとに戻したら完成ですね(^^)
$$\begin{eqnarray}&&(x+y)^2+6(x+y)+5\\[5pt]&=&A^2+6A+5\\[5pt]&=&(A+5)(A+1)\\[5pt]&=&\{(x+y)+5\}\{(x+y)+1\}\\[5pt]&=&(x+y+5)(x+y+1)\cdots(解) \end{eqnarray}$$
次の式を因数分解せよ。
$$x^2-(y+1)^2$$
この問題では、\((y+1)\)の部分をまとめておくと、\(〇^2-△^2=(〇+△)(〇-△)\)の形にすることができますね。
$$\begin{eqnarray}&&x^2-(y+1)^2\\[5pt]&&A=y+1とおくと\\[5pt]&=&x^2-A^2\\[5pt]&=&(x+A)(x-A)\\[5pt]&=&\{x+(y+1)\}\{x-(y+1)\}\\[5pt]&=&(x+y+1)(x-y-1)\cdots(解) \end{eqnarray}$$
次の式を因数分解せよ。
$$x^4-8x^2-9$$
この問題では\(x^2\)を1つのかたまりとして考えると良いです。
$$\begin{eqnarray}&&x^4-8x^2-9\\[5pt]&=&(x^2)^2-8x^2-9\\[5pt]&&A=x^2とおくと\\[5pt]&=&A^2-8A-9\\[5pt]&=&(A-9)(A+1)\\[5pt]&=&(x^2-9)(x^2+1)\\[5pt]&=&(x^2+1)(x+3)(x-3)\cdots(解) \end{eqnarray}$$
次の式を因数分解せよ。
$$4x^2+4x+1-y^2$$
パッと見たところ、同じ式もないし…で困っちゃいますね(^^;)
でも、よく見てみると…
$$\begin{eqnarray}&&\color{red}{4x^2+4x+1}-y^2\\[5pt]&=&\color{red}{(2x+1)^2}-y^2\\[5pt] \end{eqnarray}$$
この部分を因数分解することができます。
すると、\((2x+1)\)の部分を置き換えするとOKだっていうことに気が付きますね(^^)
$$\begin{eqnarray}&&4x^2+4x+1-y^2\\[5pt]&=&(2x+1)^2-y^2\\[5pt]&&A=2x+1とおくと\\[5pt]&=&A^2-y^2\\[5pt]&=&(A+y)(A-y)\\[5pt]&=&\{(2x+1)+y\}\{(2x+1)-y\}\\[5pt]&=&(2x+y+1)(2x-y+1)\cdots(解) \end{eqnarray}$$
練習問題（置き換え）
次の式を因数分解せよ。
$$5(x+1)^2-8(x+1)-4$$
次の式を因数分解せよ。
$$(x^2-x)^2-(x+8)^2$$
次の式を因数分解せよ。
$$25x^2-a^2+8a-16$$
【発展】次数の低い文字で整理する因数分解
文字が複数あるのに置き換えができない…困った！
というときには、次数の低い文字について整理するようにしましょう。
次の式を因数分解せよ。
$$x^2+xy-5x-y+4$$
パッと見たときにどうやら置き換えはできそうにないですね。
そんなときには、式を次数の低い文字で整理してみましょう。
今回の式であれば
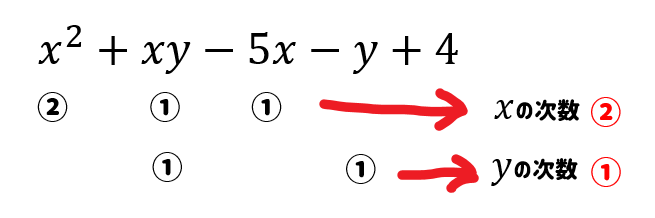
\(y\)の次数が低いので、\(y\)について式を整理していきましょう。
次数や式の整理について不安な方は、こちらの記事をご参考に！
⇒ 降べきの順のやり方をイチから！同じ次数や定数項はかっこでくくるようにしよう
$$\begin{eqnarray}&&x^2+xy-5x-y+4\\[5pt]&=&(x-1)y+(x^2-5x+4)\\[5pt]&=&(x-1)y+(x-4)(x-1)\\[5pt]&=&(x-1)\{y+(x-4)\}\\[5pt]&=&(x-1)(x+y-4)\cdots(解) \end{eqnarray}$$
このように次数の低い文字で式を整理すると、なんとなく道筋が見えてくるようになります。
あとはその道筋に沿って因数分解を続けていけばOKです。
困ったときには式の整理！
次の式を因数分解せよ。
$$x^2-xy-2y^2-x-7y-6$$
今回の問題では、\(x,y\)ともに次数が2となっています。
こういう場合にはどちらの文字で整理してもOKですが、基本的には\(x\)で整理していくとよいでしょう。
$$\begin{eqnarray} &&x^2-xy-2y^2-x-7y-6\\[5pt]&=&x^2-(y+1)x-2y^2-7y-6\\[5pt]&=&x^2-(y+1)x-(2y^2+7y+6)\\[5pt]&=&x^2-(y+1)x-(2y+3)(y+2)\end{eqnarray}$$
ここまで持ってくることができれば、あとは式のたすき掛けをやっていくことになります。
$$\begin{eqnarray}&&x^2-(y+1)x-(2y+3)(y+2)\\[5pt]&=&\{x-(2y+3)\}\{x+(y+2)\}\\[5pt]&=&(x-2y-3)(x+y+2)\cdots(解) \end{eqnarray}$$
多項式のたすき掛けはちょっと難しいですが、大事な問題なのでたくさん練習しておきましょう！
★参考動画★
練習問題（文字で整理）
次の式を因数分解せよ。
$$x^2y+y^2z-y^3-x^2z$$
次の式を因数分解せよ。
$$x^2+2xy+y^2+5x+5y+6$$
答え
$$(x+y+3)(x+y+2)$$
\(x\)に着目してまとめると
$$\begin{eqnarray}&&x^2+2xy+y^2+5x+5y+6\\[5pt]&=&x^2+(2y+5)x+(y^2+5y+6)\\[5pt]&=&x^2+(2y+5)x+(y+3)(y+2) \\[5pt]&=&(x+y+3)(x+y+2)\cdots(解)\end{eqnarray}$$
【発展】組み合わせによる因数分解
ときには項の組み合わせを考えることで因数分解ができるようになるパターンもあります。
次の式を因数分解せよ。
$$x^3-5x^2-4x+20$$
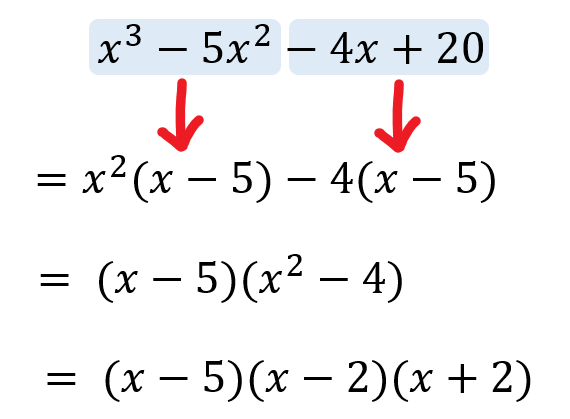
このように、部分的に項を組み合わせて共通因数などをくくってみましょう。
すると因数分解の道筋が見えてくるはずです。
練習問題（組み合わせ）
次の式を因数分解せよ。
$$x^3+6x^2+12x+8$$
【発展】平方の差をつくる因数分解
次の式を因数分解せよ。
$$x^4+4x^2+16$$
置き換えを利用しても、\(A^2+4A+16\)となり、ここから先ができずに困ってしまいます。
こういうときには平方の差を作るという考え方を利用してみましょう。
\(x^4\)と\(16\)に注目して、平方の形に変形してやります。
$$\begin{eqnarray}&&x^4+4x^2+16\\[5pt]&=&(x^4+8x^2+16)-4x^2\\[5pt]&=&(x^2+4)^2-(2x)^2\\[5pt]&=&\{(x^2+4)-2x\}\{(x^2+4)+2x\}\\[5pt]&=&(x^2-2x+4)(x^2+2x+4)\cdots(解) \end{eqnarray}$$
平方の形を作るというのはちょっと難易度が高いです。
文章で式変形について解説するのもちょっと難しい(^^;)
こちらに参考動画を用意しているので参考にしてみてください！
まとめ！
高校の因数分解はパターンが多いね。
たくさん練習して、解法を身につけておきましょう。
ザっと説明をしてきましたが、分かりにくい点などありましたらコメント欄からご要望ください。
その場合には動画解説もつけようと思いますので(^^)
コメントを残す