中学3年生に向けに、2学期の中間テストのポイントについてまとめていきます!
中3の2学期…
ラストバトルです!!
受験で重視される内申点
これが加味される最後の期間となるのが中3の2学期です。
ここで頑張って良い成績が取れるかどうか
それが受験の結果を左右すると言っても過言ではありません。
さぁ!
気合を入れて中間テストの対策に臨もうではありませんか!
2学期中間テストに出題される単元!
2学期中間テストに出題される単元は、主に以下の2つです。
- 二次方程式
- 二乗に比例する関数
※進路の早い学校では、これらに加えて相似な図形が含まれる場合もあります。
さすが中3の2学期…
そんなに簡単な内容ではありません。
それぞれの単元をしっかりと学習して準備しておきましょう。
二次方程式の出題ポイント
二次方程式の出題は以下の2点になります。
- 二次方程式の解法
- 二次方程式の利用
文章問題を読み解いて、二次方程式を立てることができるかどうか。
この2点を問われることになります。
二次方程式の解法
二次方程式を解くと言っても
これが厄介なんだ…
二次方程式は解き方がたくさんある!!
- 平方根を使って解く
- 因数分解を使って解く
- 解の公式を使って解く
- 平方完成を使って解く
それぞれの解き方の解説はこちらを参考にしてね
そして…
二次方程式を見て、どの解き方を利用すれば良いのかを判断して解いていかないといけません。
これはね
慣れるまでは、至難の業です。
何度も何度も練習を重ねて
ようやく見分けがつくようになります。
だから、ひたすら練習あるのみです!
学校の教科書やワークを使ってたくさん練習しておきましょう。
ここがきっちりと解けるようになると
テストの点数が安定してくるはずなので
今回の中間テストにおいては、まず二次方程式の計算を優先してマスターしておこう。
こちらに練習問題を解ける記事を用意しています。
ぜひ、ご活用くださいませ!
二次方程式の利用
二次方程式の解法をマスターしたら
次は利用問題に挑戦していきましょう。
二次方程式の文章問題は、正直…
超簡単だ★
一次方程式や連立方程式のときのように
速さや割合を利用した問題がありません。
更に、ほとんどがパターン化されたものばかりになります。
学校ワークに載っている問題を一通り解けるようになれば、テストでもしっかりと得点していくことができるでしょう。
花壇の道幅に関する文章問題は、鉄板の問題です。
これは出題される可能性が非常に高いので、必ず対策しておきましょう。
また、箱に関する問題もよく見かけますね。
こちらも難しくはありませんんおで、一度は解いておきましょう。
二次方程式の利用は難しくない!
だから、諦めずに挑戦していこう。
利用問題は配点が高く設定されていることが多いから
ここが得点できるようになると
驚くほど点数が伸びるようになるぞ!
ファイトだ!
二乗に比例する関数の出題ポイント
二乗に比例する関数の出題は以下の2点になります。
- \(y=ax^2\)の式を使って、関係式を作る
- 放物線のグラフを書く、読み取りをする
- 変域、変化の割合
- 利用問題
ちょっと難しく感じるかもしれません。
だけど、1つ1つの解法については
二次方程式を解くよりも楽勝です。
ちょっとやり方を覚える必要はあるかもしれませんが
しっかりと対策すれば、必ず解けるようになりますよ!
式を作る
\(y=ax^2\)を使って式を作る問題は必ず出題されるでしょう。
こちらの記事にて、1から解説をつけています。
ここに書いてある問題がすべて解けるようになればテストでは得点できるでしょう。
また、ここの問題では二次方程式の知識を利用することもあります。
そういう意味でも、まずは二次方程式を完璧にしておくことがおススメです。
グラフを書く
放物線のグラフを書く問題も必ず出題されます。
グラフの書き方は、決して難しいわけではありません。
しかし、何度か練習しておかないと
キレイに書くことはできないでしょう。
さすがにグラフが汚過ぎればバツにされてしまうこともあります。
数学が得意だからグラフの書き方は分かるぜ!
という方であっても放物線をキレイに書く練習はしておきましょう。
また、解説記事の中でも触れていますが
放物線、軸、頂点
という用語はテストで問われることもあります。
しっかりと漢字で書けるように練習しておきましょう。
変域、変化の割合
関数の問題ではおなじみ
変域、変化の割合です。
こちらもテストには出題されるでしょう。
入試問題でもよく出題される問題となっているので、必ず解けるようにしておきましょう。
変域、変化の割合…
名前からして難しそうと敬遠してしまう人もいますが
解き方を知ってしまうと
え?こんなに簡単な問題だったの!?
と、驚くこともあります。
特に、変化の割合を求めるときの裏ワザ公式!
これは学校で教えてくれないこともあるので
ここだけでこっそり学んじゃいましょw
利用問題
二乗に比例する関数の利用問題において
以下の2つはしっかりとおさえておきましょう。
んー
ぶっちゃけ、難しくないね。
ただただ文章で問題を出されているっていうだけで
やっていることは式を作って値を求めるっていうだけ!
ここはサクッと得点しちゃいましょう。
しっかりと時間をかけて対策をしてほしいのは
放物線と直線が交わる部分の面積を求めるという問題!
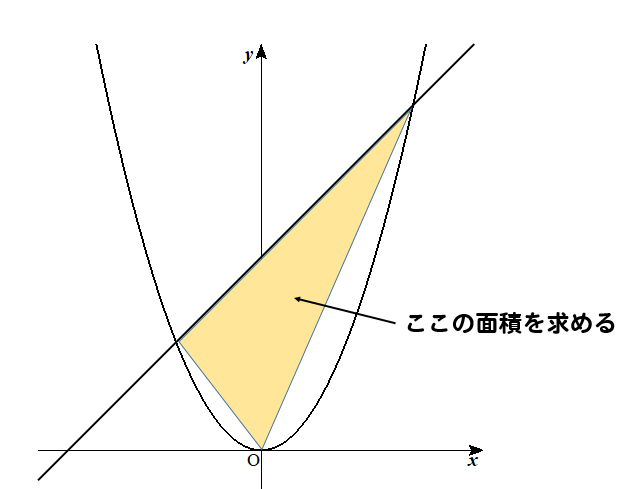
これは入試でも必須の問題となっており
定期テストでも出題される可能性は非常に高い!
それに、答えを求めるためには一次関数の知識も要するということで…
出題者側としては、すっごく嬉しい問題なんだよね。
この1問を出せば、いろいろなことを同時に問うことができるから。
この問題の解き方について
スタディサプリを利用している方は
中3数学応用という講座の中にある第21講を受講しておこう!


この解説を見ておけば
解き方についてはバッチリのはずだ!
まとめ
中3の2学期は本当に重要だ!
ここで点数を落とすようなことがあれば
他のライバルたちと差をつけられてしまうことになる。
逆に、ここでしっかりと踏ん張ることができれば
受験でもライバルたちと横一線で戦っていくことができるのだ。
死ぬ気で!
というと大げさに思うかもしれないけど
それくらい本気で頑張っていこう。
みんなが良い点数取れることを願っている!
ファイトだっ★
テスト対策はスタディサプリがおススメ

上で紹介してきたような単元、内容は全てスタディサプリを使うことで分かりやすく便利に学習することができます。
- 教科書やワークを広げて勉強を始めてみたけど書いてあることが理解できない…
- 学校の教材以外にもっとたくさんの問題に挑戦したい!
- 100点を目指すために応用問題も解けるようになりたい!
このような方たちにはスタディサプリがおススメです。
スタディサプリでは、基礎内容から発展内容までレベルに合わせた授業がたくさん用意されているので、自分のレベルに合わせて学習を進めることができます。
また、プロ講師の方々が作成した定期テストによく出るポイントをまとめた定期テスト対策講座が用意されています。
この講義を受けるだけでも、かなりの価値があります。
個人的な体感としては、テスト前にこの講義を受けさせてもらえるだけでも受講料として1万円を支払うくらいの価値はあるのではないかと感じています。
それくらい中身の濃いテスト対策講義が用意されています。
更に、高校受験対策として入試レベルの講義もたくさん用意されています。
もちろん中1、2生であっても入試講座を受講することはできます。
100点を目指すようなハイレベルな生徒さんには、入試講座に挑戦してみるのも良いかと思います。
今の段階からハイレベルな問題に触れておくことで、知識の引き出しをたくさん作ることができます。そうすることで今後の学習にも幅が広がるはずです。
様々なレベルに合わせて学習できる
テスト対策もバッチリ!
入試レベルの応用にも挑戦できる
このように様々な学習メリットがあるスタディサプリですが
なんと月額1980円(税別)で受講することができます。
しかも、数学だけでなく
英語、数学、国語、理科、社会
5教科の全講座が受講し放題で月額1980円(税別)なのです。
破格すぎますw
塾が潰れちゃう…(^^;
更に今は14日間の無料体験受講もできます。
テスト前に無料受講してしまえば、全部無料でテスト対策ができちゃいますね!
>スタディサプリの無料体験はこちら












コメントを残す