今回は小学生の算数で学習する
『倍数と公倍数』
について学習していくよ!
公倍数というのは、のちに分数の足し算、ひき算を学習していく上でとっても大切な考え方になるからちゃんと理解しておきましょう(^^)
倍数、公倍数とは
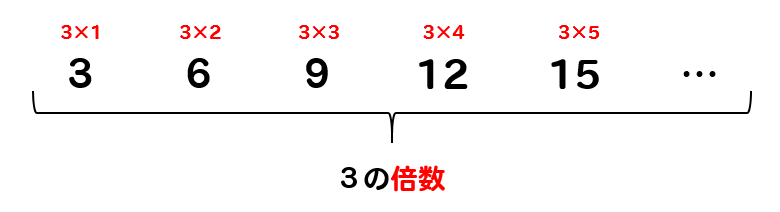
このように、ある数に整数をかけてできる数のことを倍数といいます。
例えば
5の倍数であれば
$$\Large{5, 10, 15, 20…}$$
12の倍数であれば
$$\Large{12, 24, 36, 48…}$$
といった感じですね(^^)
次に、4と6の倍数をそれぞれ見ていくと
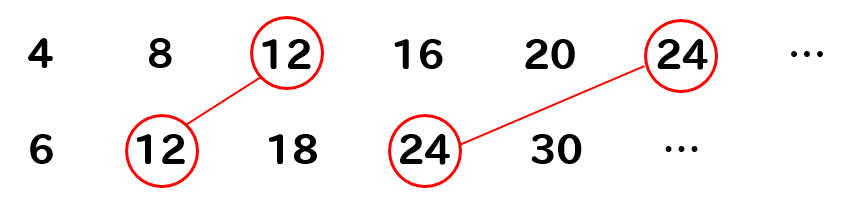
このように共通している数があるよね。
このようにそれぞれの倍数の中にある同じ数のことを公倍数といいます。
つまり4と6の公倍数は
$$\Large{12, 24, 36, 48…}$$
ということになります。
そして、大事なのがコレ
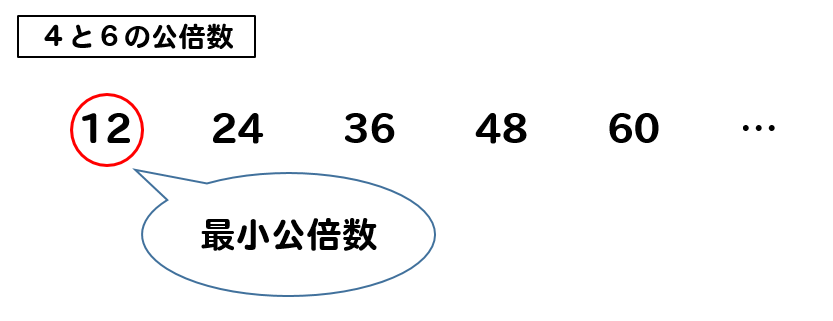
公倍数の中で、最も小さい数のことを最小公倍数といいます。
公倍数というのは
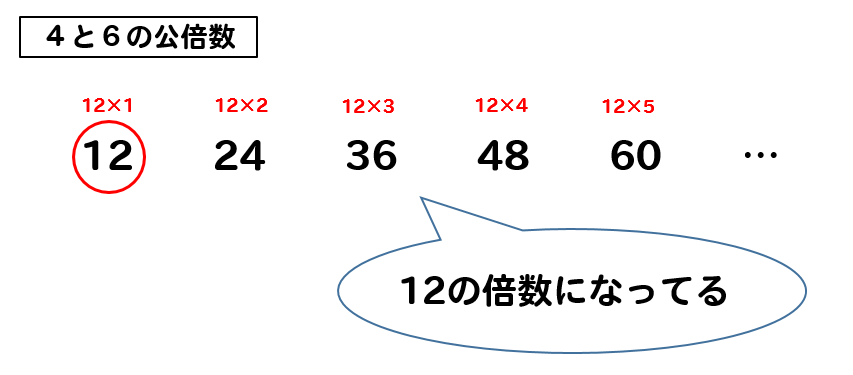
このように最小公倍数に整数をかけることで見つけていくことができるんだよね。
つまり、4と6の公倍数とは最小公倍数である12の倍数になっているってことが分かるよ!
公倍数の求め方
それでは、次に公倍数を見つける問題について見ていきましょう。
公倍数の求め方について、いくつかの方法をご紹介します。
自分に合ったやり方をマスターしていきましょう(^^)
それでは、6と8の公倍数を求めてみましょう。
求め方①
一番シンプルなやり方は、それぞれの倍数を書き出すというものです。
6の倍数を書き出す。
$$\Large{6, 12, 18, 24, 30, 36, 42, 48…}$$
8の倍数を書き出す。
$$\Large{8, 16, 24, 32, 40, 48…}$$
それぞれ書き出した数の中から共通している数を見つけていきましょう。
すると
$$\Large{24, 48, 72…}$$
が共通していることが分かります。
よって、これらの数が6と8の公倍数ということになります。
大きな数になると見つけにくくなりますよね。
そういう場合には、まず最小公倍数を見つけましょう。
今回であれば、24ですね。
最小公倍数を見つけることができれば、他の公倍数は
$$24\times 2=48$$
$$24\times 3=72$$
$$24\times 4=96$$
このように見つけていくことができます。
なので、それぞれの倍数を書き出すとき
たくさん書く必要はありません。
最小公倍数が見つかるまででOKです。
求め方②
次のやり方は、まず大きい数の倍数を書き出します。
今回であれば8の方が大きいので、8の倍数を書き出します。
8の倍数
$$\Large{8, 16, 24, 32, 40, 48…}$$
このように8の倍数が書けたら
それぞれの数が6で割り切ることができるかをチェックしていきます。
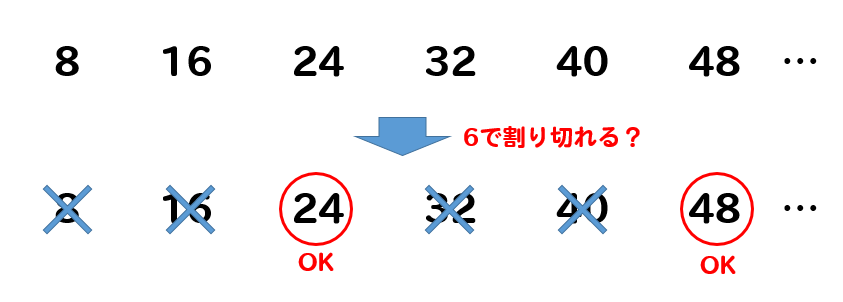
割り切ることができれば、その数が公倍数ということになります。
15と18の公倍数を求めろ!
といったように、大きい数どうしの公倍数を求めたいとき
それぞれの倍数を書き出すのが大変だよね…
そういうときには、やり方②のように
大きな数の倍数だけを書き出し
その数の中にもう一方の数で割り切れるかどうかを調べる。
という方法を使うと、少しだけ手間が省けますね(^^)
こちらのやり方も最小公倍数を見つけることができればOK
あとは最小公倍数に整数を掛けていけば残りの公倍数も見つけることができるからね!
3つの数の公倍数
次はちょっと応用問題になっちゃうんだけど
3つの数の公倍数を見つける問題について見ておきましょう。
2と3と4の公倍数を見つけましょう。
求め方①の考え方を用いると、それぞれの倍数を書き出して3つともに共通している数を見つけていけば良いです。
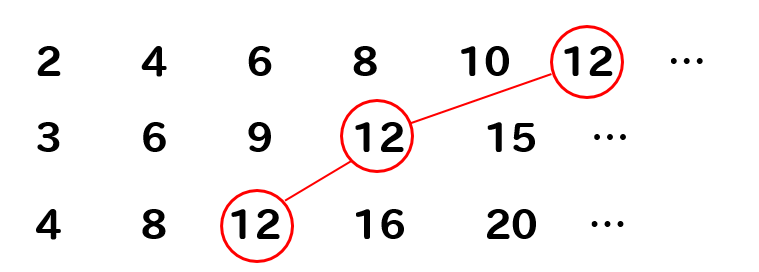
すると、最小公倍数が12だと分かりますね。
最小公倍数を見つけることができれば、あとは簡単!
$$12\times 2=24$$
$$12\times 3=36$$
$$12\times 4=48$$
このように見つけていくことができます。
よって、2と3と4の公倍数は
$$\Large{12, 24, 36, 48…}$$
ということが求まりました。
求め方②の考え方を用いて解く場合
まずは一番大きい数である4の倍数を書き出します。
そして、その数の中から3で割り切れる数と見つけます。
更に、その中から2で割り切れる数を見つけます。
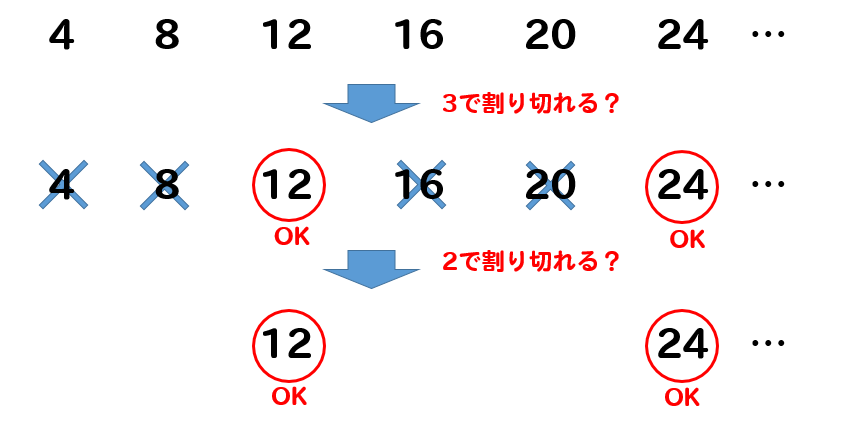
そして、残った数が3つの数の公倍数ということになります。
また、公倍数を見つける裏ワザ的なやり方もあります。
詳しくはこちらの記事をご参考に!
倍数の見分け方
次は倍数の見分け方について解説しておきます。
$$\LARGE{3585}$$
この数って何の倍数になるか分かりますか?
いやいや…数がデカくて分かんねぇよ
って思っちゃうよね(^^;)
だけどね、これをパッと見極める方法っていうのがあるんだよね
その方法をいくつか覚えておきましょう。
2の倍数の判定方法
2の倍数、つまり偶数のことですが
これは簡単!
1の位の数が\(0,2,4,6,8\)のいずれかになっていれば
その数は2の倍数となります。
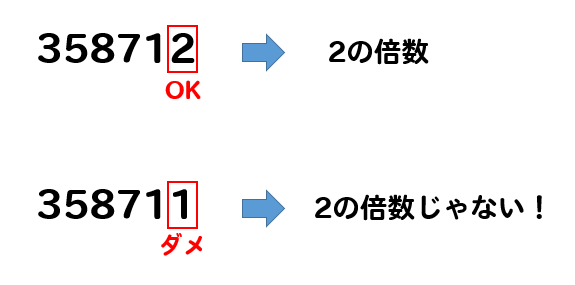
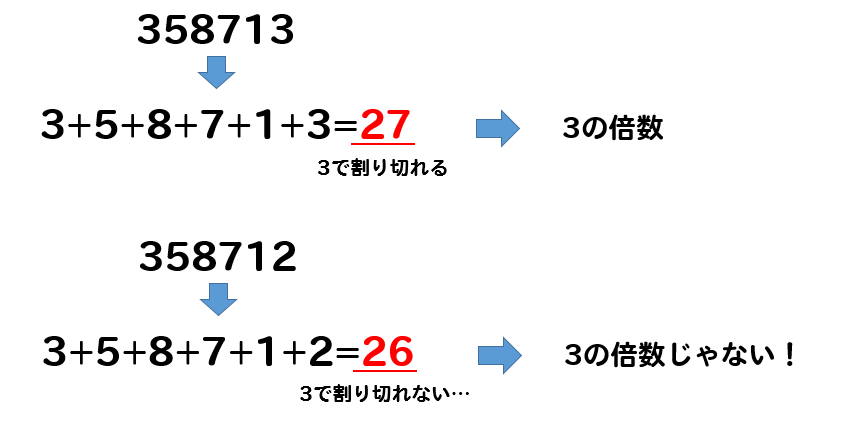
3の倍数の判定方法
各位の数を足したとき
その数が3で割り切ることができれば
その数は3の倍数になります。
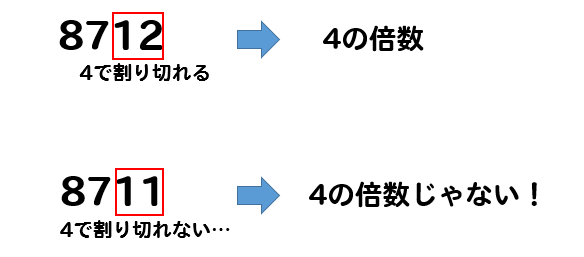
4の倍数の判定方法
下二けたの数が00または4で割り切れるとき
その数は4の倍数となります。
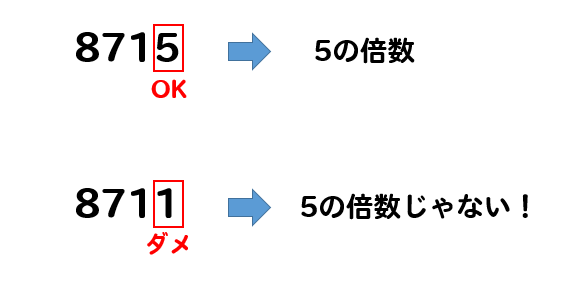
5の倍数の判定方法
一の位が0または5であれば
その数は5の倍数となります。
まとめ
お疲れ様でした!
倍数については以上となります。
公倍数を見つける問題は多くの小学生が苦手としています…
ですが、やり方を身につけた子は以降、スラスラと解くことができるようになります。
だって、別に難しいことしてるわけじゃないもんね
シンプルな計算問題をやっているだけです。
だから、手順を覚えるまでは苦労するかもしれませんが
しっかりと意味を理解して解き方をマスターできるよう繰り返し練習していきましょう。
ファイトだ(/・ω・)/

















便利で勉強になり、今後も使わせていただきます。
ありがとうございます!
少しでもお役に立てる記事を増やしていきますね(^^)
小学生でもわかりやすいです(^^)
分かる!
同じく!
お役に立てて嬉しいです!
コメントありがとうございます^^
とても詳しくて分かりやすかったです!
お役に立てたようで嬉しいです^^
他の記事もぜひ参考にしてみてくださいね!
わかりやすく教えて頂いてありがとうございます!!テストの時も頑張ります!
お役に立ててよかったです!
テストがんばってください^^