中学2年生に向けに、2学期の中間テストのポイントについてまとめていきます!
さぁ、中間テストの時期がやってまいりました。
中2の2学期と言えば…
数学が激ムズ期に突入してしまい
成績を落としてしまう人が続出する時期でもあります。
だからこそ!
他の人と差をつけることができるチャンスの時期でもあります。
しっかりと中間テストに備えて
上位をとっていこうぜ★
2学期中間テストに出題される単元!
2学期中間テストに出題される単元は、主に以下の2つです。
- 連立方程式
- 一次関数
※進路の早い学校では、これらに加えて平行と合同が含まれる場合もあります。
場合によっては、連立方程式が含まれず一次関数だけの出題になる可能性もあります。
その場合には、一次関数の細かい部分まで問われるようになるので、たくさん問題を解いて対策しておく必要がありますね。
連立方程式の出題ポイント
連立方程式は1学期の期末試験にも出題された単元になります。
そのため、2学期の中間テストには連立方程式の文章問題がメインで取り上げられることになります。
連立方程式の文章問題はバリエーションが豊かです。
- 個数と代金
- 速さ
- 割合 など
いろいろな文章問題があります。
これらを1つ1つ正確に解けるように練習しておきましょう。
文章問題は、初めて解く場合にはちょっと苦労するかもしれません。
だけど、しっかりと解説を読んで何度も練習すれば簡単に解けるようになります。
だって、同じパターンしか出題されないからね(^^)
何度も練習していれば
「あ、またこのパターンか!」
と思えるようになるはずです。
まずは学校ワークに載っている問題を完璧にしておきましょう!
このサイトでも連立文章題の解説をつけているので、良かったら参考にしてみてください。
スタディサプリを利用されている方は、中2の連立方程式の利用を受講しておきましょう。

ここでは、上で述べたような
個数と代金、速さ、割合の文章問題について分かりやすく解説してくれています。
文章題がまったく分からない…という方であっても、こちらを受講すればある程度は解けるようになるはずです(^^)

一次関数の出題ポイント!
一次関数の単元においては以下の問題が出題されます。
- 一次関数の用語★
- グラフの書き方、読み取り★
- 式の作り方★
- 変域、変化の割合★
- 一次関数の利用問題
利用問題はちょっと難しくなっちゃうので期末に回る可能性があります。
だけど、利用問題が中間に入る場合にはちょっと気合入れて対策していかんといけんぞ!
一次関数の用語
一次関数の単元において、新たに出てきた用語がありましたね。
それらがテストで問われる場合があります。
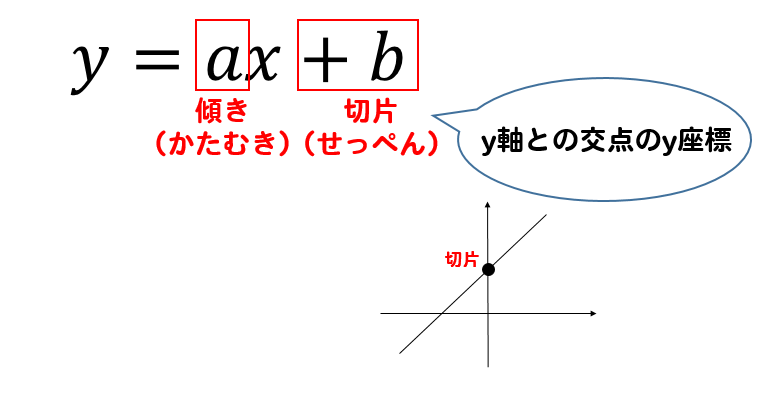
傾きと切片
これはテストで最も問われやすい用語です。
ちゃんと漢字で書けるように練習しておきましょう。
また、グラフの形にも注目
傾きが+のときには右上がりの直線
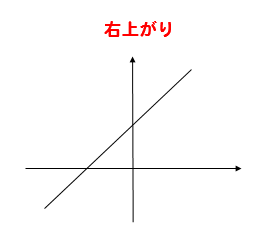
傾きが-のときには右下がりの直線
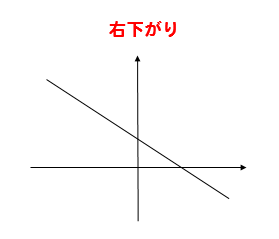
になります。
これも覚えておいてね。
右上がり、右下がり
テストに出るかもしれません。
グラフの書き方、読み取り
一次関数のグラフの書き方
そして、グラフから式を作る。
これは必ずテストに出題されます。
しかも、めっちゃ簡単★
なので、この問題に関しては得点源としていきたいです。
一次関数のグラフについては、こちらの記事で解説をつけています。
絶対にできるようにしておきましょう!
式の作り方
この問題はちょっとばかり厄介だ…
やり方を覚えることと、多少の計算力が必要になります。
できればテスト2週間前から練習を始めておきたい問題です。
こちらの記事で式の作り方について徹底解説しています。
ここに載っていることが理解できるようになればテストでは十分に戦っていくことができるでしょう。
変域、変化の割合
変域と変化の割合
この言葉を聞いただけで…
オレ、ムリだわ…

って思っちゃいがちです。
だけど、正直…この問題って簡単なんだよね。
響きが難しそうに感じるだけです。
変化の割合は次のように求めることができます。
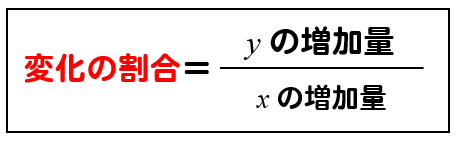
そして、ポイントなのは
一次関数において、変化の割合とは…
傾きと同じ値になる!
ということです。
これを覚えておけば簡単に問題が解けるようになるはずです。
また、\(y\)の増加量を求める問題に関しては
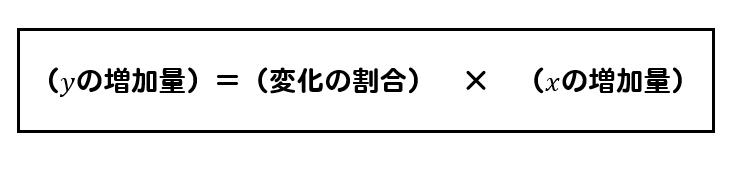
このような関係を用いて解いていくようになります。
これも覚えておきましょう。
また、変域についてはこちらの記事で解説をつけているので、しっかりと理解しておきましょう。
まとめ
2学期の中間テストは、しっかりと対策をしておかないとガクッと点数を落としてしまうことになります。
連立方程式の文章題
一次関数の式 など
これはめちゃめちゃ練習しておかないと解けませんよね(^^;)
でも、逆に言えば
点数を落とす人が続出するということは
自分が上位に上がるチャンスとも言えます。
みんな!
頑張って上位取ろうぜ★
テスト対策はスタディサプリがおススメ

上で紹介してきたような単元、内容は全てスタディサプリを使うことで分かりやすく便利に学習することができます。
- 教科書やワークを広げて勉強を始めてみたけど書いてあることが理解できない…
- 学校の教材以外にもっとたくさんの問題に挑戦したい!
- 100点を目指すために応用問題も解けるようになりたい!
このような方たちにはスタディサプリがおススメです。
スタディサプリでは、基礎内容から発展内容までレベルに合わせた授業がたくさん用意されているので、自分のレベルに合わせて学習を進めることができます。
また、プロ講師の方々が作成した定期テストによく出るポイントをまとめた定期テスト対策講座が用意されています。
この講義を受けるだけでも、かなりの価値があります。
個人的な体感としては、テスト前にこの講義を受けさせてもらえるだけでも受講料として1万円を支払うくらいの価値はあるのではないかと感じています。
それくらい中身の濃いテスト対策講義が用意されています。
更に、高校受験対策として入試レベルの講義もたくさん用意されています。
もちろん中1、2生であっても入試講座を受講することはできます。
100点を目指すようなハイレベルな生徒さんには、入試講座に挑戦してみるのも良いかと思います。
今の段階からハイレベルな問題に触れておくことで、知識の引き出しをたくさん作ることができます。そうすることで今後の学習にも幅が広がるはずです。
様々なレベルに合わせて学習できる
テスト対策もバッチリ!
入試レベルの応用にも挑戦できる
このように様々な学習メリットがあるスタディサプリですが
なんと月額1980円(税別)で受講することができます。
しかも、数学だけでなく
英語、数学、国語、理科、社会
5教科の全講座が受講し放題で月額1980円(税別)なのです。
破格すぎますw
塾が潰れちゃう…(^^;
更に今は14日間の無料体験受講もできます。
テスト前に無料受講してしまえば、全部無料でテスト対策ができちゃいますね!
>スタディサプリの無料体験はこちら













とてもわかりやすくて助かりました。