今回は、正三角形の角度を求める問題について解説していくよ！
正三角形の性質はとってもシンプルなんだけど
角度を求める問題になると
むずいかも…
と、なってしまいがちなので
今回は正三角形の角度を求める問題を
厳選した4パターンで徹底解説していきます！
今回の記事内容は、こちらの動画でも解説しています(/・ω・)/
Contents
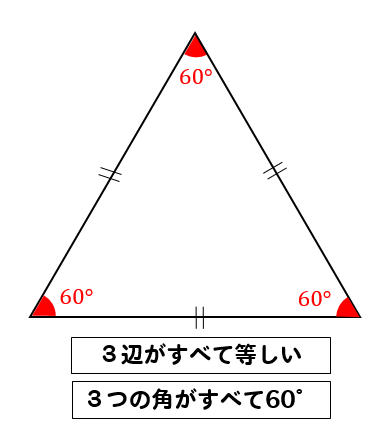
覚えておきたい正三角形の性質
- 3辺がすべて等しい
- 3つの角がすべて60°
この2つの性質をしっかりと覚えておいてください。
角度の問題なんだけど
『3辺がすべて等しい』
という辺に関する性質も使っていくからね！
忘れないように頭に入れておこう。
厳選4パターンの問題に挑戦！
それでは、正三角形の角度を求める問題をパターン別に解説していきます。
正三角形の基本パターン
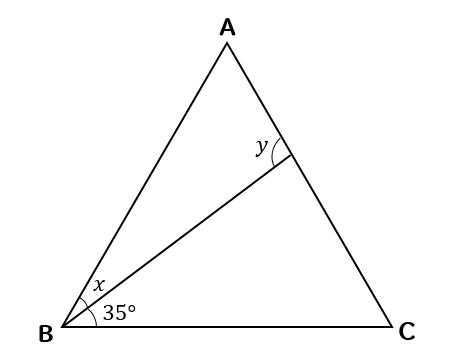
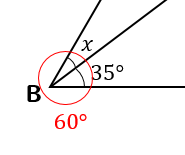
△ABCが正三角形のとき、\(∠x, ∠y\)の大きさを求めなさい。
答え
$$∠x=25°$$
$$∠y=95°$$
正三角形の角は60°という性質を利用すれば
\(x\)の角は
$$x=60-35=25°$$
と求めることができます。
そして、外角の性質を利用すれば
\(y\)の大きさは
$$∠y=35+60=95°$$
と求めることができます。
正三角形の角が60°になるということを覚えておけば大丈夫な問題でしたね！
正三角形の融合パターン
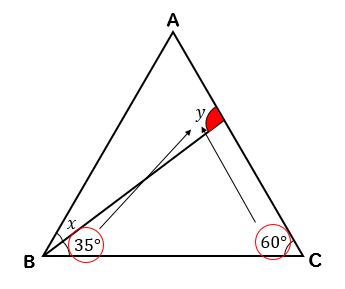
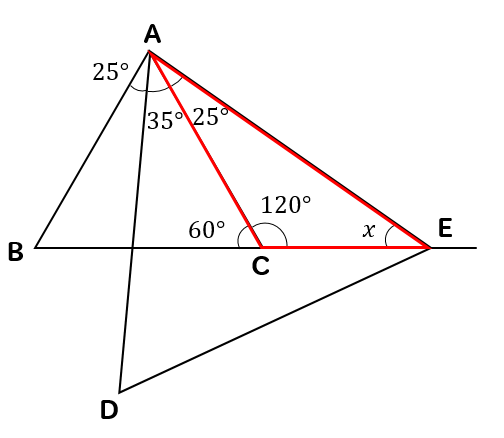
△ABC、△ADEが正三角形のとき、\(∠x\)の大きさを求めなさい。
答え
$$∠x=35°$$
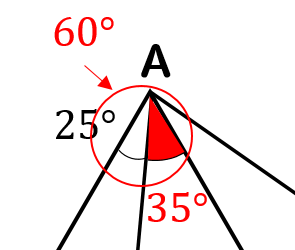
まず、△ABCの正三角形に注目すると
1つの角は60°になることから
赤い部分が35°になることがわかります。
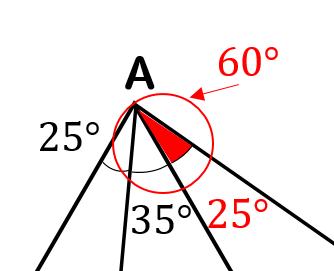
次は△ADEの正三角形に注目すると
赤い部分が25°になることがわかります。
そして、△ACEに注目して
三角形の内角の和が180°になるということから
$$x=180-(120+25)=35°$$
と求めることができます。
正三角形が重なっている場合には
それぞれの角が60°になっていることを意識して
少しずつ\(x\)の角に近づくように
いろんな角を求めていきましょう。
正方形との融合パターン
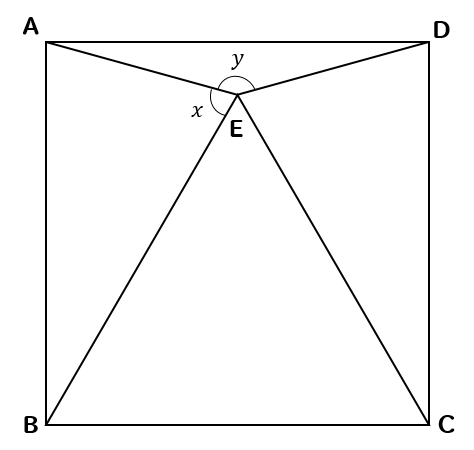
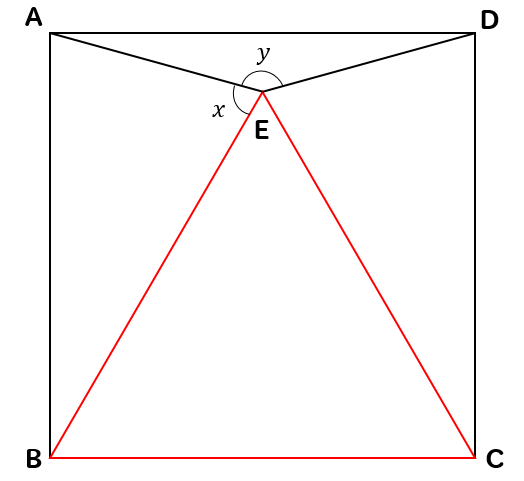
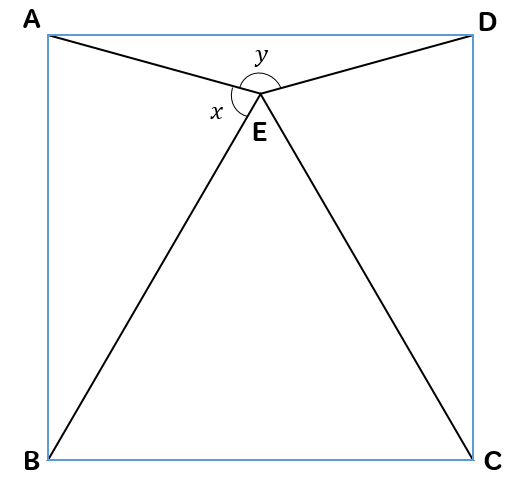
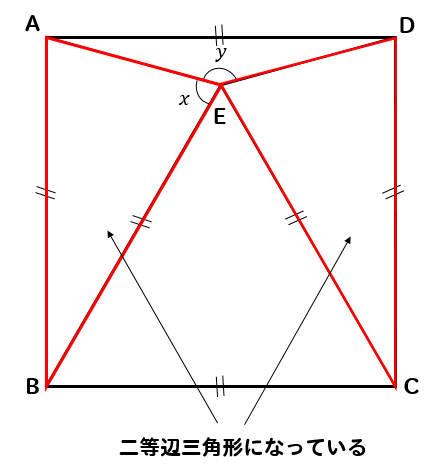
四角形ABCDは正方形、△BCEは正三角形のとき、\(∠x, ∠y\)の大きさを求めなさい。
答え
$$∠x=75°$$
$$∠y=150°$$
正三角形と正方形の融合問題を考えるときには
辺の関係性がとても重要です。
では、この図形において
どの部分が同じ長さになっているか考えてみましょう。
△EBCは正三角形なので、赤い部分はすべて同じ長さになります。
$$EB=BC=CE$$
四角形ABCDは正方形なので、青い部分はすべて同じ長さになります。
$$AB=BC=CD=DA$$
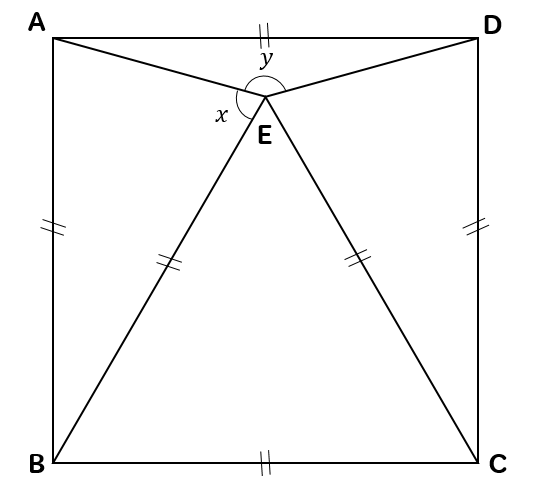
そして、この2つの特徴を組み合わせると
$$AB=BC=CD=DA=EB=CE$$
同じ長さになるとことがたくさんある！ということがわかります。
すると
△ABEと△ECDは二等辺三角形になっているということに気づきますね。
このことを利用して、角の大きさを考えていきます。
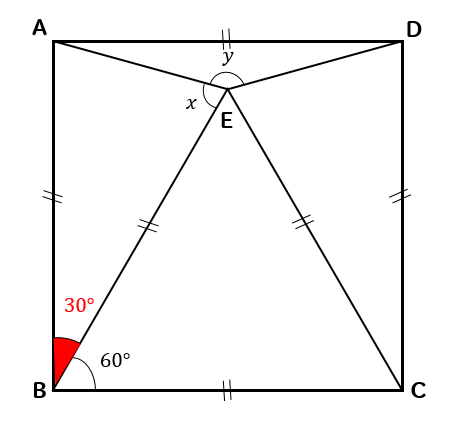
正方形の角は90°になるので
△ABEの頂角は30°になることがわかります。
そして、\(∠x\)は△ABEの底角なので
$$180-30=150$$
$$x=150\div 2 =75°$$
\(x\)の大きさがわかったら
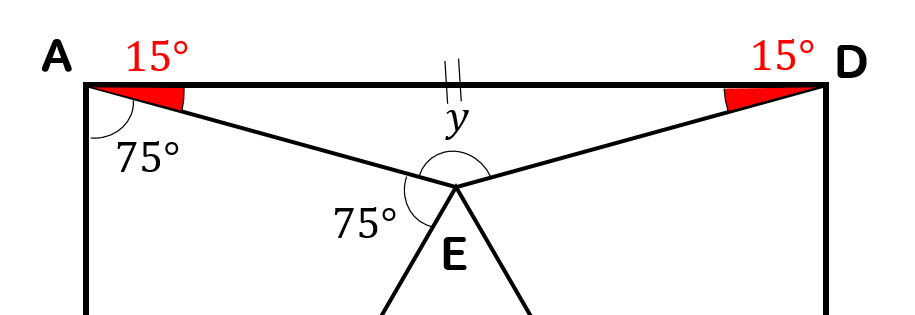
次は△AEDに注目します。
すると、\(∠DAE,∠ADE\)はそれぞれ\(15°\)とわかるので
$$y=180-(15+15)=150°$$
とわかりました。
正三角形と正方形の融合問題では
辺の大きさが等しいところを見つけていくと
二等辺三角形が見つかるので
そこをヒントに角度を求めていくと良いです(^^)
ひし形との融合パターン
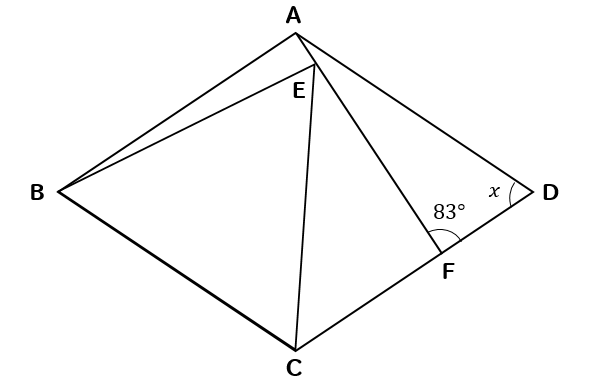
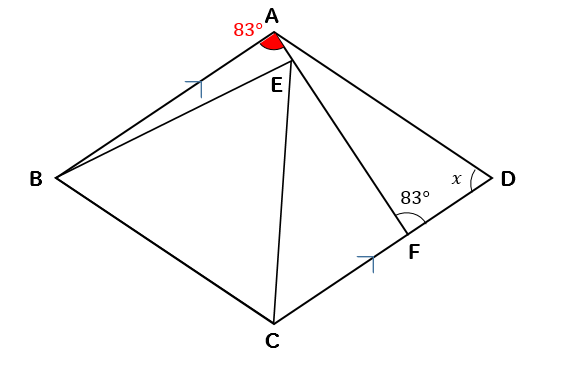
四角形ABCDはひし形、△BCEは正三角形のとき、\(∠x\)の大きさを求めなさい。
答え
$$∠x=74°$$
まずはこの問題を解くために
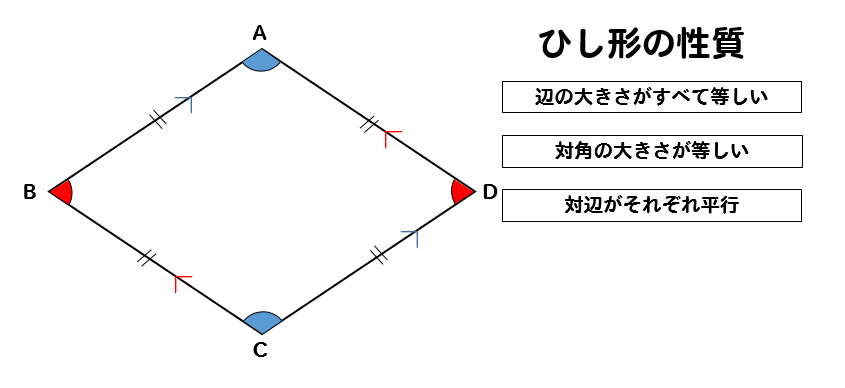
ひし形の性質を復習しておきましょう。
今回問題の中で利用していく性質は
『辺の大きさがすべて等しい』
『対角の大きさが等しい』
『対辺がそれぞれ平行』
それでは以上3点を頭に入れておいて
問題を見ていきましょう。
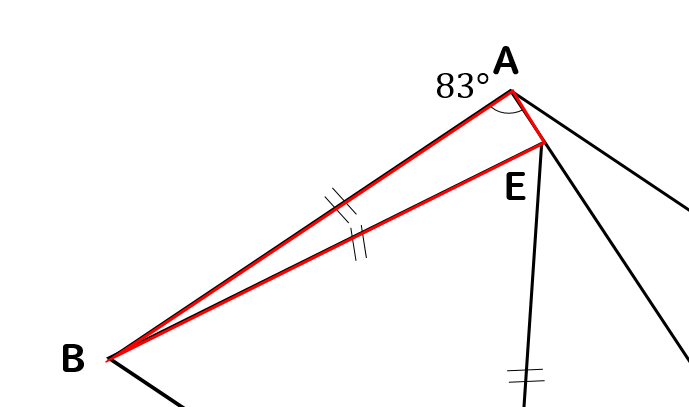
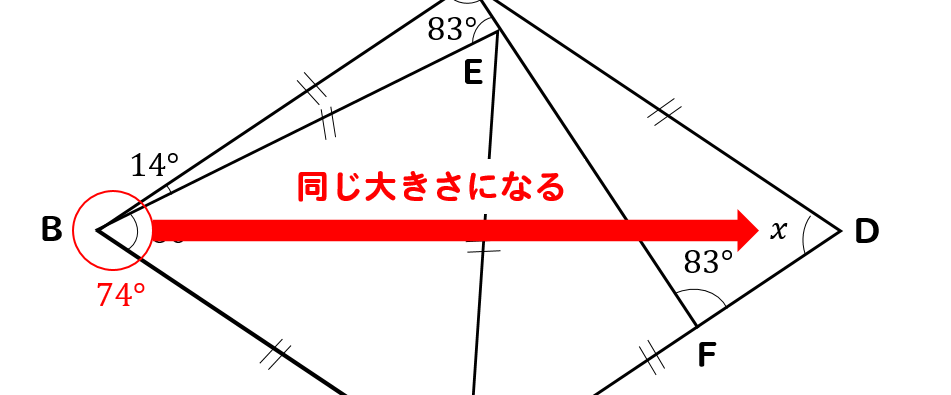
まず、AB//DCより錯角は等しくなるので
\(∠BAE＝83°\)となります。
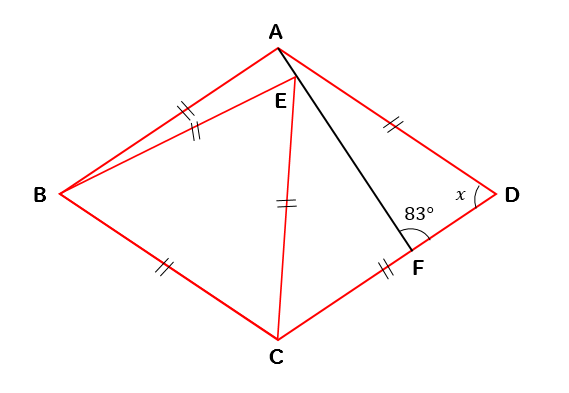
次にひし形、正三角形の性質から
辺の長さが等しいところが、このように見つかります。
すると△ABEは二等辺三角形になることがわかります。
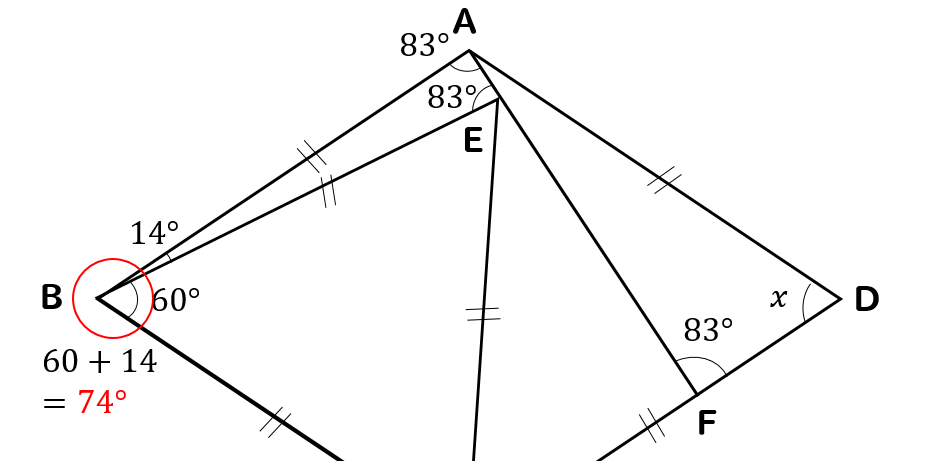
よって、△ABEに注目すると
それぞれの角はこのようになります。
∠Bの大きさが74°とわかりました。
ひし形の対角は同じ大きさになることから
$$∠x=74°$$
となります。
ひし形と正三角形の融合問題は少し難しめですが
ひし形の3つの性質を覚えておけば大丈夫！
しっかりと覚えておきましょう。
正三角形の角度問題 まとめ
お疲れ様でした！
正三角形の性質としては
このように単純な性質しかないので
問題としては、いろんな図形との融合で出題されがちです。
- 正三角形どうしの融合の場合
60°の角になるところをしっかりと見つけていくこと
- 正方形との融合の場合
同じ長さになるところを見つけて、二等辺三角形を利用する
- ひし形との融合の場合
ひし形の性質を利用しながら考えていく
これらのポイントをしっかりと覚えておいてくださいね！
正三角形の角度をマスターしたら
次は二等辺三角形にも挑戦してみましょう！
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説！
【直角三角形】証明問題の書き方とは？合同条件の使い方を徹底解説！
正三角形の角度 正方形、ひし形との融合問題を解説！←今回の記事
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、以下の内容を無料でお届けします！
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
コメントを残す