今回は、三角形の合同条件について
詳しく解説をしていきます。
- 三角形の合同条件とは?
- 合同な三角形を見つけてみよう!
というテーマでお話していきます。
これから
合同の証明問題をやっていく上で
大切となってくる基礎部分なので
しっかりと理解しておきましょう!
合同な図形の基本性質については、こちらの記事を参考にしてね!
三角形の合同条件とは?
合同な図形とは
ぴったり重なる図形のことでしたね。

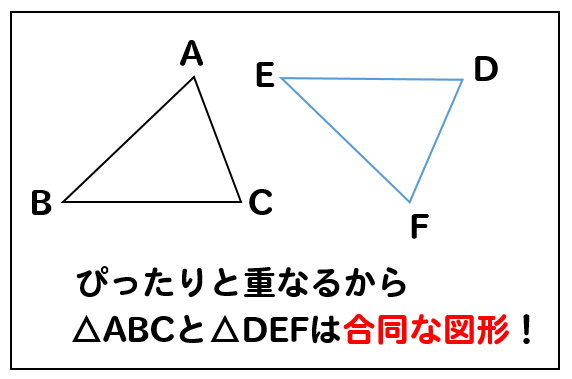

でもね
三角形に関しては
わざわざ図形を動かして
ぴったり重なるかどうかを確かめなくても
君たちは合同だ!!


と確かめる方法がありました。
それが『三角形の合同条件』というものです。
それぞれの三角形の長さや角の大きさを比較して
次の3つのいずれかの条件を満たせば
2つの三角形は合同だということがわかります。
3組の辺がそれぞれ等しい
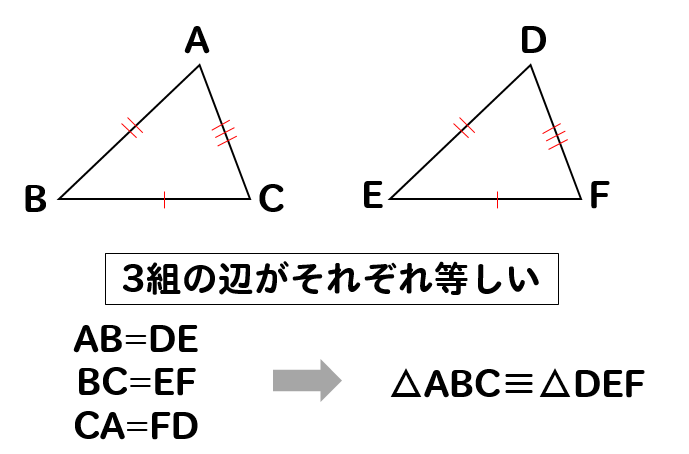

2つの三角形を比較したときに
3つとも辺の長さが等しければ、合同だということがわかります。
2組の辺とその間の角がそれぞれ等しい
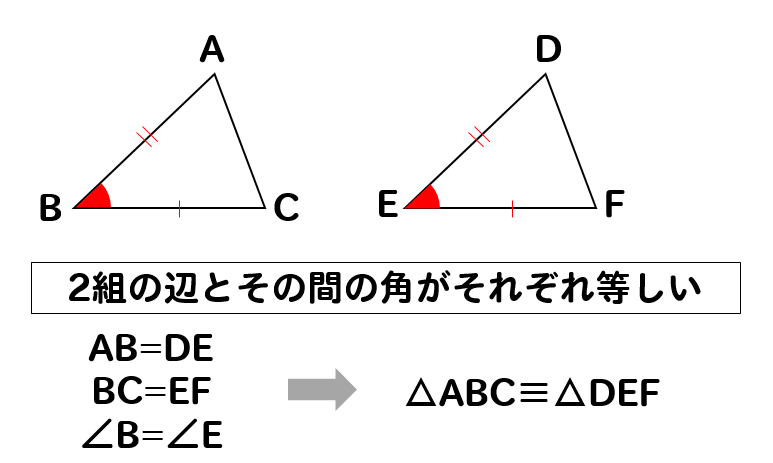

2つの三角形を比較したときに
2組の辺とそれに挟まれている間にある角が等しければ、合同だということがわかります。
1組の辺とその両端の角がそれぞれ等しい


2つの三角形を比較したときに
1組の辺の長さが等しくて
その辺の両端の角がそれぞれ等しくなっていれば、合同だということがわかります。
これら3つの条件をしっかりと覚えておいてください。
定期テストには、必ず出題されるからね!
それでは
合同条件を使って
合同な三角形を見つける練習をやってみましょう!
合同な三角形を見つける問題に挑戦!
それでは次の図形の中に隠れている
合同な三角形を見つけてみましょう!


次の図で合同な三角形を見つけ、そのときに使った合同条件を書きなさい。
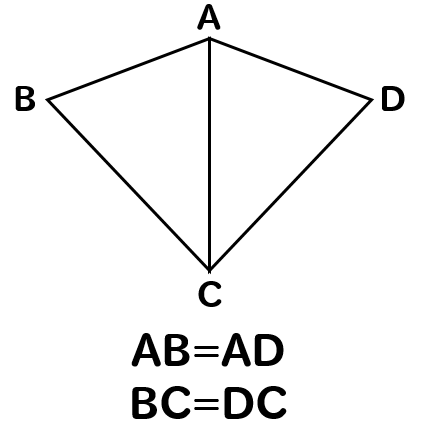

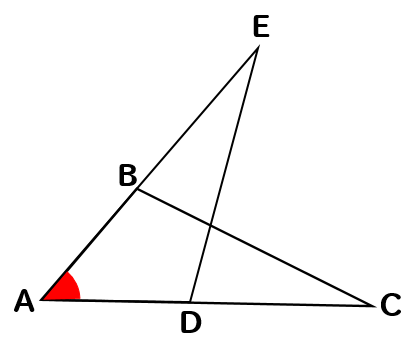
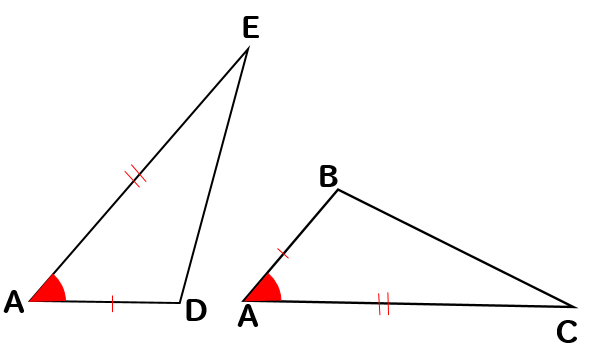
△ABCと△ADCに注目して
問題文にある情報を書き込むと
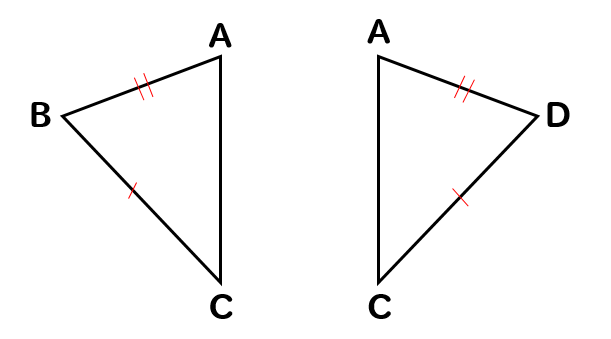

このように2組の辺がそれぞれ等しいことがわかります。
だけど
これだけだと、合同条件のどれにも当てはまらないので
まだ2つの三角形が合同になるとは言い切れません。
なので
他にも等しくなるところがないなか~
と、等しくなるような辺や角の大きさを探していきます。
すると
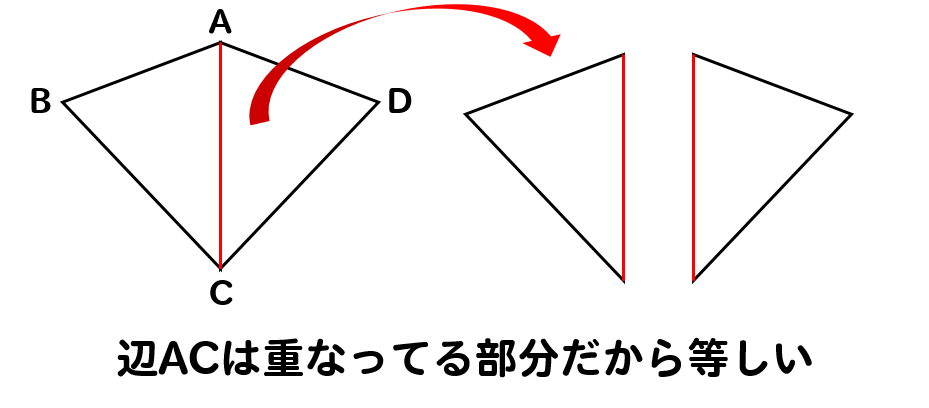

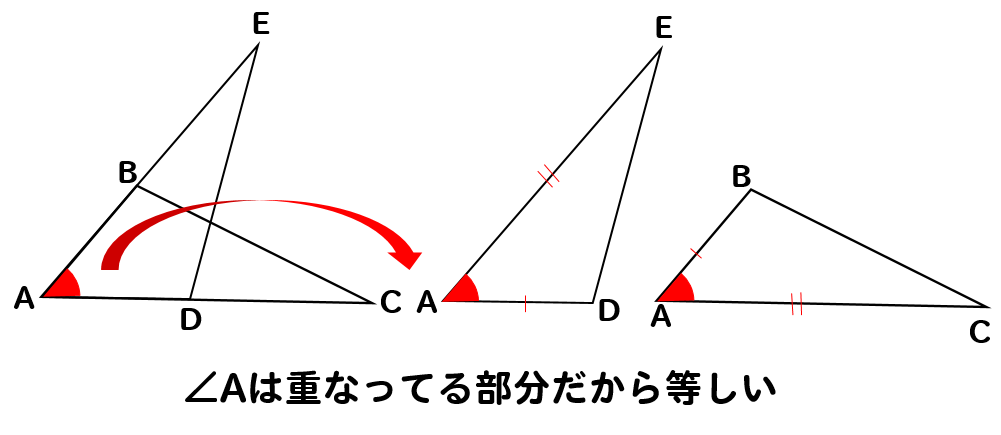
辺ACは重なっている部分だから
△ABCと△ADCの2つに分けて書いたとしても
等しくなるはずだよね!
だから
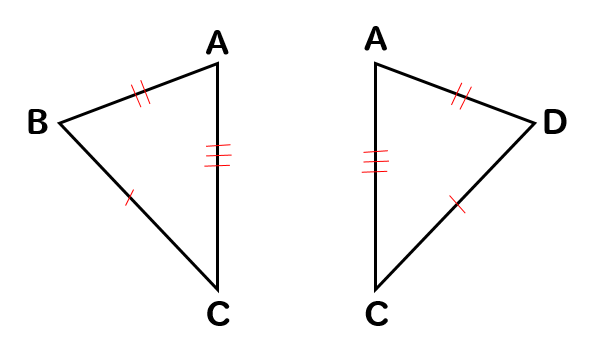

このように
『3組の辺がそれぞれ等しい』ので
△ABC≡△ADCということがわかりました。
合同な三角形を見つけていく問題では
問題文に書いてある情報だけでは
条件を満たさないことが多いので
図形をよーく見て、等しくなるような辺や角を自分で見つけていく必要があります。
今回のように
重なっている辺は等しい!
という情報は良く使うので覚えておきましょう。
ちなみに
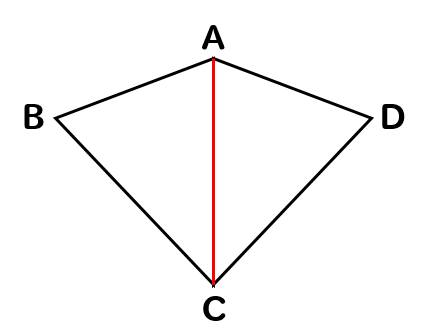

辺ACのように重なっている辺のことを
『共通な辺』というから
これも覚えておこう!
では、こんな感じで
いろんな図形において
合同な三角形を見つける練習をしていきましょう。


演習問題で理解を深める!
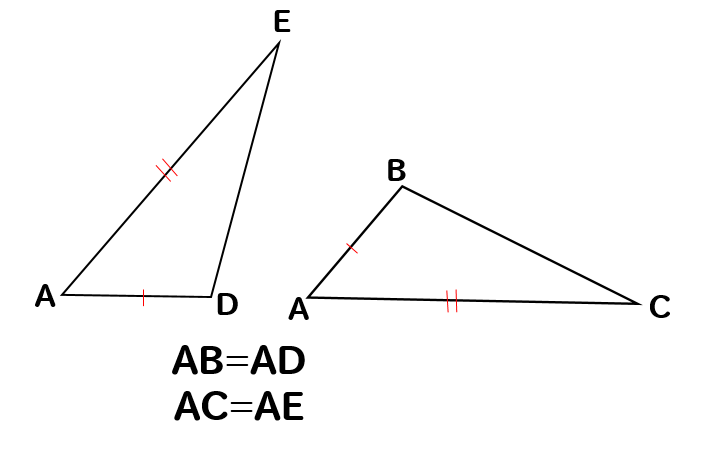
次の図で合同な三角形を見つけ、そのときに使った合同条件を書きなさい。
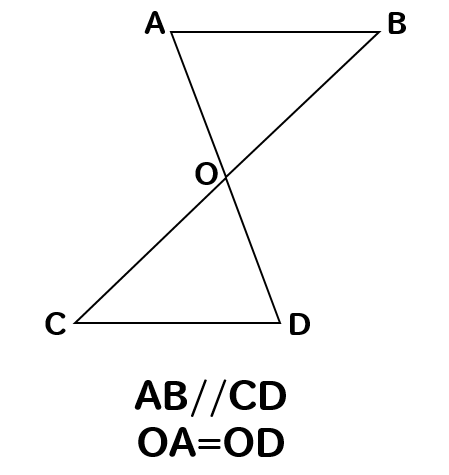

次の図で合同な三角形を見つけ、そのときに使った合同条件を書きなさい。
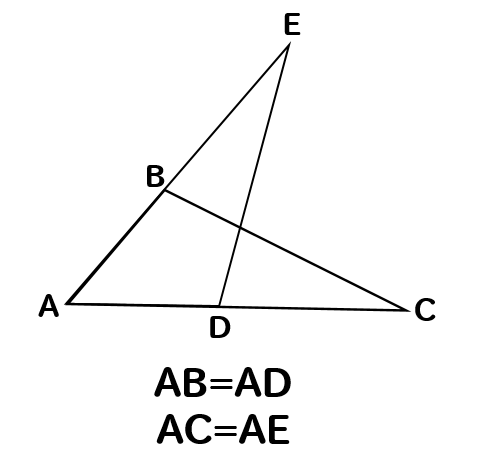

合同な図形の見つけ方 まとめ
お疲れ様でした!
三角形の合同条件はもうバッチリですか??
- 3組の辺がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 1組の辺とその両端の角がそれぞれ等しい
これから証明問題へ進んでいく上で
必要となってくるものなので
ぜーーーーったいに覚えておきましょう!
また、合同な図形を見つける練習をしてもらいましたが
その中で、問題文にある情報以外に
等しくなる辺や角を見つける作業をやってもらいましたよね。
等しくなるところを
自分で見つけるという作業が、証明問題をマスターしていく上で
すごく重要なものになります。
共通な辺だから
共通な角だから
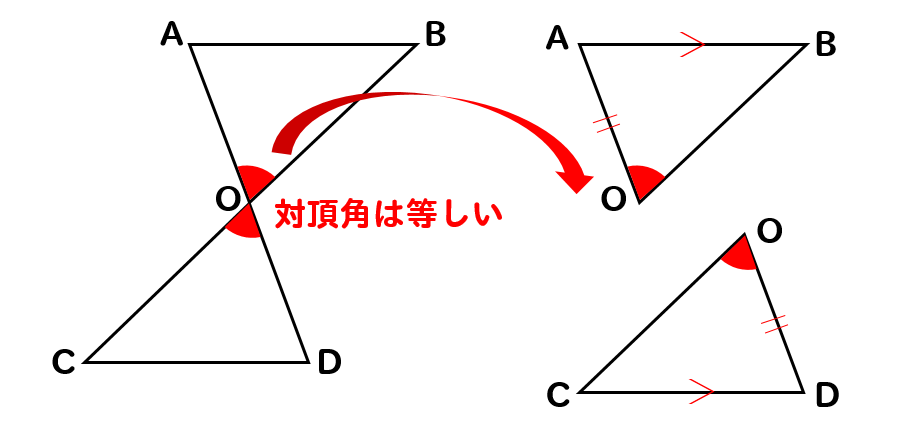
対頂角は等しいから
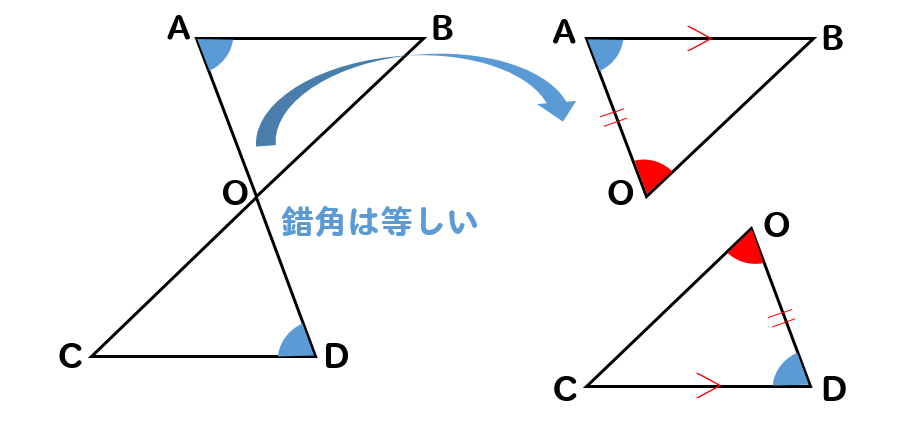
平行で錯角は等しくなるから などなど
問題文には書いてなくても
自分で発見できる情報はたくさんあります。
こういったことを利用して
問題文以外の情報を読み取れるようになると
証明問題は楽勝です!


今回学習したことをしっかりと復習して
証明問題へと挑戦していきましょう!
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
ファイトだー(/・ω・)/
三角形の合同条件を使って、合同な三角形を見つける方法!←今回の記事
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!

















コメントを残す