高校数学で学習する式の展開の単元から
置き換え、組み合わせ、計算順序
を工夫して展開する問題を解説します。
展開の基礎である以下の公式は使いこなせるものとしてお話を進めていきます。
【乗法公式】
$$(a+b)^2=a^2+2ab+b^2$$
$$(a-b)^2=a^2-2ab+b^2$$
$$(a+b)(a-b)=a^2-b^2$$
$$(x+a)(x+b)=x^2+(a+b)x+ab$$
$$(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$$
ちょっと不安だなぁという方はこちらの記事で復習しておいてくださいね!
また、\((a+b)^3\)、\((a+b+c)^2\) といったよく出てくる展開については
こちらの記事をご参考ください!
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
式の展開の工夫~置き換えを利用~
次の式を展開せよ。
$$(1)(x+y+4)(x+y-4)$$
$$(2)(x^2+2+x)(x^2-1+x)$$
$$(3)(x+y-1)(x-y+1)$$
問題の解説~置き換えのやり方~
次の式を展開せよ。
$$(1)(x+y+4)(x+y-4)$$
3つと3つの展開…ちょっとややこしいですね。
こういう場合には、それぞれのかっこの中に同じ部分がないか探してみましょう。
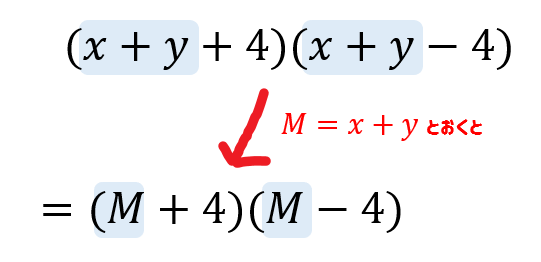
\(x+y\)という部分が同じであることが見つかりますので、ここを文字で置き換えてあげましょう。
すると、3つと3つでややこしかった展開の式が、2つと2つの見慣れた形に変換できましたね。
$$\begin{eqnarray} &&(x+y+4)(x+y-4)\\[5pt]&=&(M+4)(M-4)\\[5pt]&=&M^2-16\\[5pt]&&ここでMをx+yに戻す。\\[5pt]&=&(x+y)^2-16\\[5pt]&=&(x^2+2xy+y^2)-16\\[5pt]&=&x^2+2xy+y^2-16\cdots(解)\end{eqnarray}$$
次の式を展開せよ。
$$(2)(x^2+2+x)(x^2-1+x)$$
さぁ、今回もかっこ内に同じ部分を見つけて置き換えをしていきましょう。
でも、あれ…\((\color{red}{x^2}+2\color{red}{+x})(\color{red}{x^2}-2\color{red}{+x})\)
同じ部分がちょっと離れてるけど…という場合でも大丈夫。
かっこ内の順番を変えれば良いだけの話なので、別に気にすることなく置き換えちゃってください。
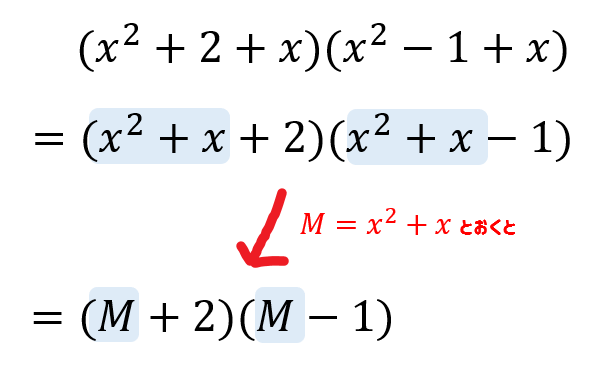
$$\begin{eqnarray} &&(x^2+2+x)(x^2-1+x)\\[5pt]&=&(M+2)(M-1)\\[5pt]&=&M^2+M-2\\[5pt]&&ここでMをx^2+xに戻す。\\[5pt]&=&(x^2+x)^2+(x^2+x)-2\\[5pt]&=&(x^4+2x^3+x^2)+(x^2+x)-2\\[5pt]&=&x^4+2x^3+2x^2+x-2\cdots(解)\end{eqnarray}$$
次の式を展開せよ。
$$(3)(x+y-1)(x-y+1)$$
この問題はすごく大事!!
パッと見たときに同じ部分が見つからないのです。
しかし、よく見てみると…
右かっこにある\(-y+1\)という部分は、マイナスでくくることによって
$$\large{-y+1=-(y-1)}$$
と形を変えることができます。
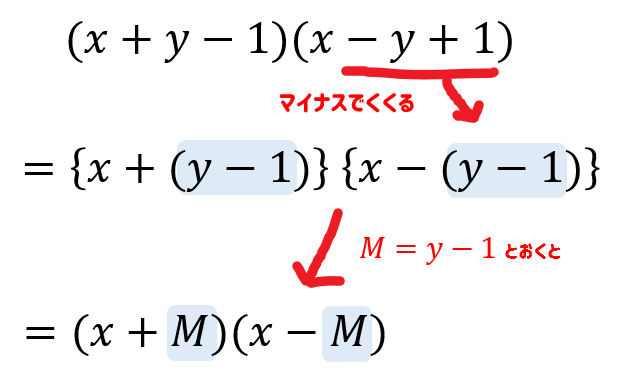
$$\begin{eqnarray} &&(x+y-1)(x-y+1)\\[5pt]&=&(x+M)(x-M)\\[5pt]&=&x^2-M^2\\[5pt]&&ここでMをy-1に戻す。\\[5pt]&=&x^2-(y-1)^2\\[5pt]&=&x^2-(y^2-2y+1)\\[5pt]&=&x^2-y^2+2y-1\cdots(解)\end{eqnarray}$$
このように、マイナスでくくって同じ部分を見つけるというのはちょっぴり難易度が高いです。
それだけにテストでも出題されやすいので、たくさん練習して解けるようにしておきたい。
あれ、同じ部分がないぞ…と思ったら、どこかをマイナスでくくってみるという考えを持っておきましょう。
式の展開の工夫~組み合わせ、計算順序を考える~
次の式を展開せよ。
$$(1)(x-2)^2(x+2)^2$$
$$(2)(x+3)(x-2)(x+4)(x-1)$$
問題の解説~計算の順序~
次の式を展開せよ。
$$(1)(x-2)^2(x+2)^2$$
何も考えずに展開をしようとすると…
$$(x-2)^2(x+2)^2=(x^2-4x+4)(x^2+4x+4)$$
となってしまいますね。ちょっと複雑になっちゃいました(^^;)
これで解けなくもないのですが、ちょっと工夫をすることで簡単に解けるようになります。
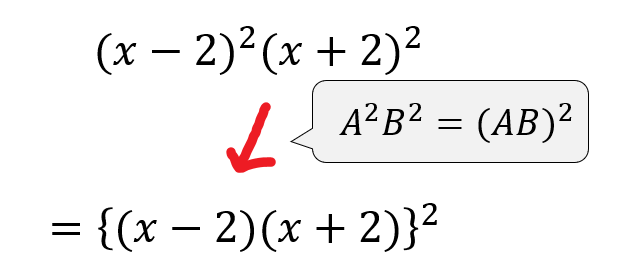
このように2乗と2乗のかけ算は、それぞれをかけてから2乗してもOK。
という計算ルールを用いて、計算の順序を工夫してから展開していきましょう。
$$\begin{eqnarray}&&(x-2)^2(x+2)^2\\[5pt]&=&\{(x-2)(x+2)\}^2\\[5pt]&=&(x^2-4)^2\\[5pt]&=&x^4-8x^2+16\cdots(解) \end{eqnarray}$$
すると、少しだけ簡単に展開することができましたね(^^)
問題の解説~組み合わせ~
次の式を展開せよ。
$$(2)(x+3)(x-2)(x+4)(x-1)$$
よ、4つもあるんだけど!!って感じですね(^^;)
だけど、これは組み合わせを工夫することで簡単に展開することができます。
今回の問題であれば、4つある内、次のような組み合わせで展開をしていきます。
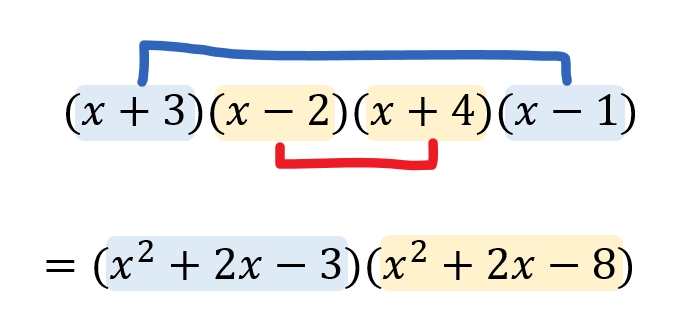
なぜ、このような組み合わせで展開したのか分かりますか?
その答えは、展開した後の式に注目すると理解できます。

そうですね、この組み合わせで展開したことにより、同じ部分を作ることに成功したのです!
すると、この後の展開では置き換えが利用できるため、少しだけ計算がラクになりますね。
$$\begin{eqnarray}&&(x+3)(x-2)(x+4)(x-1)\\[5pt]&=&(x^2+2x-3)(x^2+2x-8)\\[5pt]&&M=x^2+2xとおくと\\[5pt]&=&(M-3)(M-8)\\[5pt]&=&M^2-11M+24\\[5pt]&=&(x^2+2x)^2-11(x^2+2x)+24\\[5pt]&=&x^4+4x^3+4x^2-11x^2-22x+24\\[5pt]&=&x^4+4x^3-7x^2-22x+24\cdots(解) \end{eqnarray}$$
このようにかっこが4つあるような展開では、同じ部分が出てくるような組み合わせを見つけて計算していきましょう。
まとめ
それでは、最後にまとめておきましょう。
複雑な展開では、同じ部分を見つけて置き換えを利用しましょう。

置き換えにおいては、マイナスでくくる必要があるかもしれません。
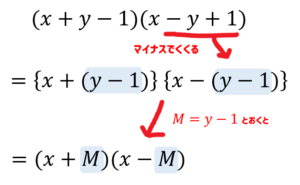
2乗と2乗の展開においては、まずはそれぞれをかけてから、あとで2乗する。
計算順序を工夫すると計算がラクになります。
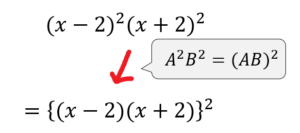
かっこが4つあるような展開では、同じ部分が出てくるような組み合わせを見つけて計算していきましょう。
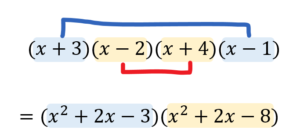


















コメントを残す