今回は高校数学Ⅰで学習する
『不等式』という単元から
こういった問題の解き方を解説していきます。
$$-8<3x-5<4$$
3つの式がつながっている不等式!
これはどのように解いていけば良いのでしょうか。
連立不等式についてはこちらの動画でも解説してます!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
高校メルマガ講座の無料登録はこちら!
3つの不等式の解き方
次の不等式を解け。
$$-8<3x-5<4$$
このように3つの式がつながっている不等式を解くためには
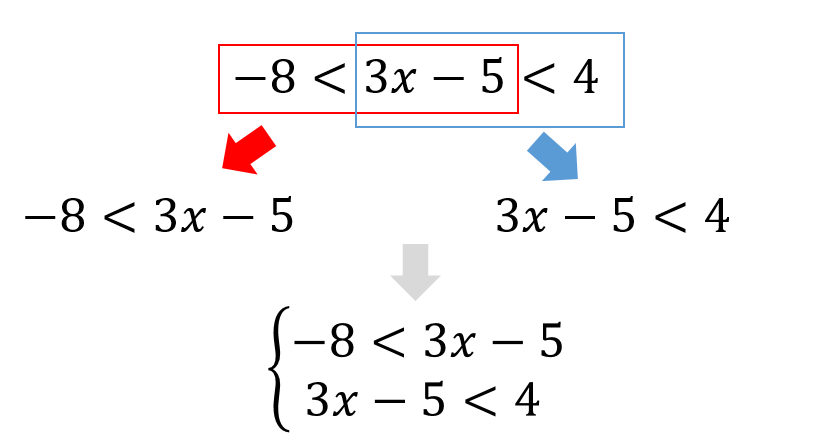
2つの不等式に分けて、連立不等式として解いていきます。
3つの不等式のうち
小<中<大
⇒ 小<中
⇒ 中<大
というように2つの不等式にわけます。
小<大とは、しないので気を付けてね!
それでは、連立不等式を解いていきます。
まずは\(-8<3x-5\)を解きます。
$$-8<3x-5$$
$$-3x<-5+8$$
$$-3x<3$$
$$x>-1$$
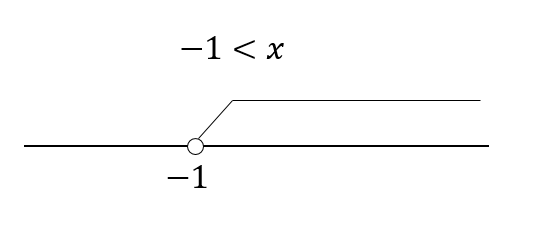
次に\(3x-5<4\)を解いていきます。
$$3x-5<4$$
$$3x<4+5$$
$$3x<9$$
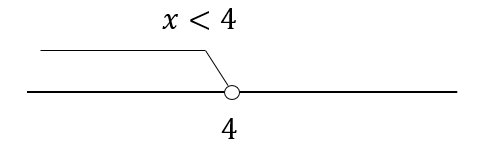
$$x<3$$
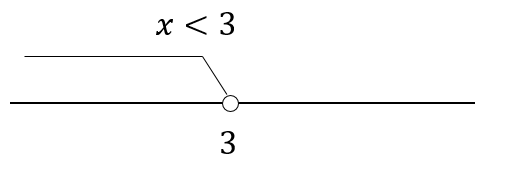
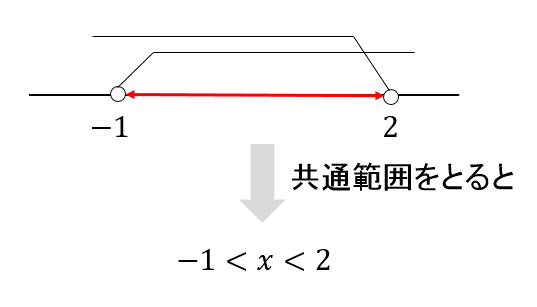
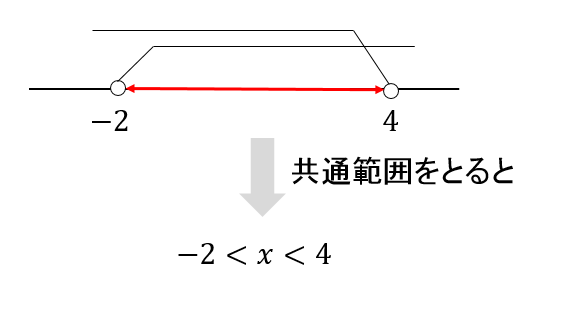
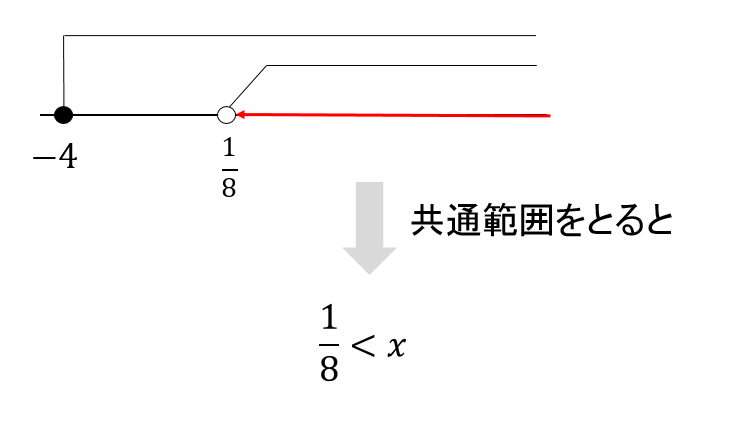
そして、2つの答えの共通範囲をとると
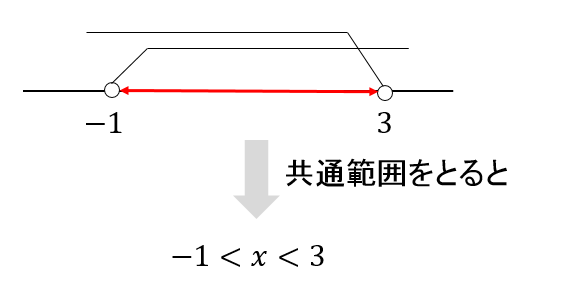
このように、答え\(-1<x<3\)を求めることができます。
3つの式がつながっている不等式の解き方をまとめておきます。
- 小<中、中<大にわけて2つの不等式を作る
- 2つの不等式を連立させて解く
以上!
ちなみに、今回の問題のように
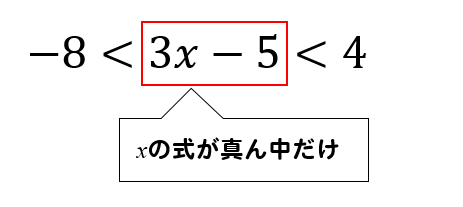
小、中、大の式の中にxを含む式が1つしかないときには
連立不等式を解かなくても
このように計算してやることができます。
$$-8<3x-5<4$$
各辺に5を加える
$$-8+5<3x-5+5<4+5$$
$$-3<3x<9$$
各辺を3でわる
$$-1<x<3$$
明らかにこっちの方が楽だよね(^^;
でも、こうやって解ける問題ばかりが出題されるわけではないから
必ず連立不等式で解けるようにしておきましょう。
このような不等式は、連立不等式にしないといけないからね!

それでは、理解を深めるために演習問題に挑戦してみましょう。
演習問題で理解を深める!
次に不等式を解きなさい。
$$(1) -3<2x-1<3$$
$$(2) 3x-8<5x-4<4x$$
$$(3) -6x+2<2x+1≦4x+9$$
それでは、それぞれ解説していきます。
$$(1) -3<2x-1<3$$
$$(2) 3x-8<5x-4<4x$$
$$(3) -6x+2<2x+1≦4x+9$$
3つの不等式解き方 まとめ
演習問題お疲れ様でした!
3つの式がつながっている不等式は
小<中、中<大
というように2つの不等式に分けて
連立不等式として計算するということでした。
この3つの不等式は
二次関数の最大値、最小値の場合分けなどで
出てくることが多いので
地味な問題ではありますが
確実に解けるようにしておきたいですね(^^)



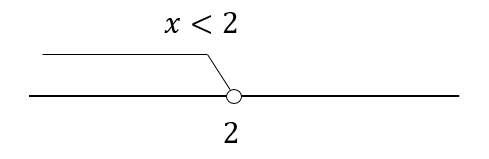















ありがとう