$$\Large{(a+b+c)^2}$$
このようにかっこの中に3つの項が含まれているときの展開ってどうやって計算すればいいんだっけ？
あまり見慣れない形なだけに、戸惑ってしまう方も多いんじゃないでしょうか？
今回の記事では、かっこ内に3つの項が含まれているときの2乗の展開を楽に計算してしまうハートの公式！というラブリーな公式をご紹介します。
今回の記事内容は、こちらの動画でも解説しています。
3つの項の二乗を楽にするハートの公式
3つの項を含む二乗の展開は、以下のようになります。
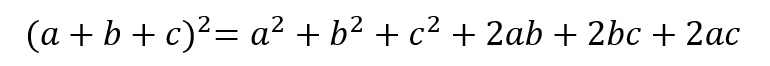
長々していて、ちょっと覚えにくいよね…
てか、これのどこがハートなの！？
的確なツッコミありがとうございますｗ
なぜ、これをハートの公式と呼ぶのかというと
このようにハートの形を作ることで公式を導くことができるからなんですね！
とっても便利なので、私は学生時代からずーっと愛用しています＾＾
それでは、ハートの公式を使って実際に計算問題をやってみましょう。
次の式を展開しなさい。
$$\Large{(x+2y-3)^2}$$
これをハートの公式に当てはめて展開すると次のようになります。
$$(x+2y-3)^2$$
$$=x^2+(2y)^2+(-3)^2+2\cdot x\cdot 2y+2\cdot 2y\cdot (-3)+2\cdot x\cdot (-3)$$
$$=x^2+4y^2+9+4xy-12y-6x$$
このように展開することができます。
公式を使ったら簡単ですね＾＾
公式を使わず展開したい！
ハートの公式！？
なんじゃそりゃ！
そんなふざけたもん使わずにオレは硬派に問題を解きたいんじゃ！
そんなあなたへ
ハートの公式を使わずに展開する方法も紹介しておきます。
$$(a+b+c)^2$$
やっぱりかっこの中に3つも項があるとややこしいです。
ということで、\(X=a+b\)というように置き換えを利用して
$$=(X+c)^2$$
このようにかっこ内の項を2つにして考えていきましょう。
すると、あとは今まで見慣れた2乗の展開公式を利用すればOKです。
$$=X^2+2Xc+c^2$$
$$=(a+b)^2+2(a+b)c+c^2$$
$$=a^2+2ab+b^2+2ac+2bc+c^2$$
となりました！
ちょっと順番を変えてやれば
$$=a^2+b^2+c^2+2ab+2bc+2ac$$
上で紹介したハートの公式と同じ形を導くことができましたね。
公式を覚えるのはちょっと…という方は、このように置き換えを利用して展開してみてください＾＾
まとめ
お疲れ様でした！
$$\Large{(a+b+c)^2}$$
このようにかっこ内に3つの項が含まれている2乗の展開は
- ハートの公式を利用する
- 置き換えを利用する
どちらか好みに合わせて計算していきましょう！
私はハートの公式一筋でやっています。
だって…
ハートの公式
なんだかロマンティックで素敵じゃない♡
コメントを残す