【中3数学】複雑な式の展開をマスターしよう！

こんにちは！数スタの小田です。

今回は中学3年生で学習する展開の計算の中で、もっとも計算ミスが起こりやすい複雑なものを取り上げます。

それがコレ！

$$\Large{2(a-2)(a+3)-(a-4)^2}$$

うげぇ…

かっこがたくさんあって複雑じゃ…

って感じですね(^^;)

実際、式の展開を習ったばかりの生徒さんに解かせてみると、計算ミスの嵐だったりします…(+_+)

なので、そういったミスを引き起こさないためにも今回の記事では途中式をていねいに書きながら指導していきます。

みなさんも途中式を意識しながらていねいに解き進めていきましょう！

ちなみに今回の記事は、こちらの動画でも解説しています(/・ω・)/

複雑な式の展開では、計算の順序に注意！

今回のような複雑な式の展開では、計算をする順序が非常に大切です。

かっこの外についている数や符号は置いといて

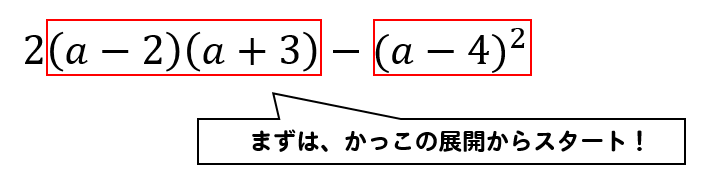
かっこの展開を先にしてやりましょう！

そして、かっこの前に数や符号がついているときには、展開した式にかっこをつけたままにしておきましょう。

次に、かっこを外して同類項どうしをまとめていけば完成です！

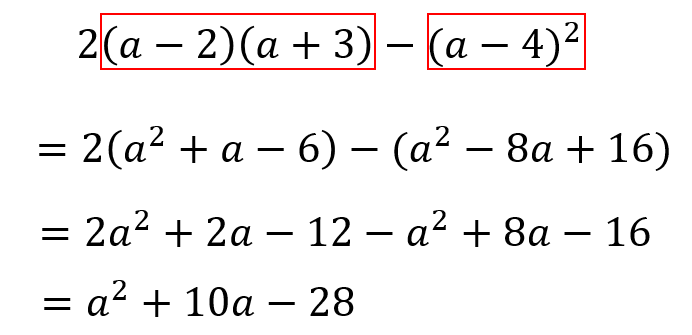
複雑な式の展開を計算する手順をまとめておきましょう。

見た目は難しそうな式ですが、しっかりと手順を守って計算していけば簡単に解くことができますよ(^^)

ただ、計算ミスが起こりやすい計算ではあるので、たくさん練習をして身につけていきましょう！

演習問題で理解を深める！

要点まとめ＆追加演習を用意しました！

演習問題はバッチリ解けましたか？？

ここの計算は模試や入試にもよく出題されるので完璧に仕上げておきたいですね！

というわけで、今回の内容をいつでもサクッと復習できるように「要点まとめ＆追加演習プリント」を用意しました。試験前に取り組むことで、ミスしやすいポイントなどを確認することができますよ＾＾

数スタのメルマガ講座に登録してくれた方に、こちらの追加演習をプレゼントしています！

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で利用できますので、下のフォームから登録をお願いします＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定です。

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

今回のような複雑な式の展開が計算できるようになれば、この単元はバッチリです！

まだ不安が残る方やスラスラと乗法公式を使いこなせていないという方は、ひたすら練習あるのみです！

学校のワークや参考書を使って、計算しまくろう！

ファイトだー(/・ω・)/