今回は、中1で学習する正負の数から
分数計算のやり方について解説していきます。
分数の計算は苦手な人が多いよね＞＜
多くの人が間違えてしまうような問題を取り上げて解説していくので、この記事を通して、分数の計算方法をしっかりと身につけていきましょう！
今回の記事はこちらの動画でも解説しています(/・ω・)/
分数の加法・減法（たし算・ひき算）
それでは、まず分数の加減について見ていきましょう。
$$\LARGE{-\frac{1}{4}+\frac{2}{3}}$$
$$\LARGE{\frac{1}{5}-\frac{1}{2}}$$
分数のたし算、ひき算では分母を揃える通分という作業が必要でしたね。
分母が揃ったら、分数を合体させて分子同士を計算していきましょう！
$$\Large{-\frac{1}{4}+\frac{2}{3}}$$
$$\Large{=-\frac{3}{12}+\frac{8}{12}}$$
$$\Large{=\frac{-3+8}{12}}$$
$$\Large{=\frac{5}{12}}$$
計算終わり！！
通分ができれば、あとは普通の計算と同じように考えればOKですね！
ひき算の場合も同じです。
通分をして、分子同士をそれぞれ計算していきましょう。
$$\Large{\frac{1}{5}-\frac{1}{2}}$$
$$\Large{=\frac{2}{10}-\frac{5}{10}}$$
$$\Large{=\frac{2-5}{10}}$$
$$\Large{=-\frac{3}{10}}$$
計算終わり！！
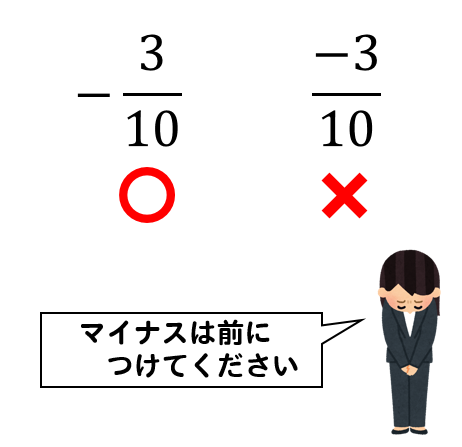
マイナスの符号は分数の前に持ってくるようにしようね。
分数の乗法・除法（かけ算・わり算）
次は分数の乗除について見ていきましょう。
$$\LARGE{\frac{4}{3}\times \left(-\frac{15}{8}\right)}$$
$$\LARGE{\left(-\frac{1}{6}\right) \div \left(-\frac{4}{9}\right)}$$
乗除では、符号決めがポイントでしたね。
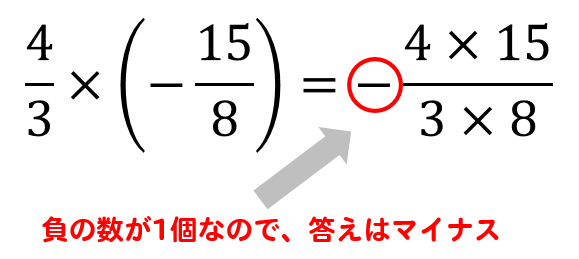
計算する数の中に負の数（ー）が奇数個（１個、３個、５個…）⇒ 答えの符号はマイナス計算する数の中に負の数（ー）が偶数個（０個、２個、４個…）⇒ 答えの符号はプラス
まず、答えの符号を決めて
そこから分母、分子どうしをそれぞれ計算していきます。
計算途中で、約分もしてやると楽になりますね(^^)
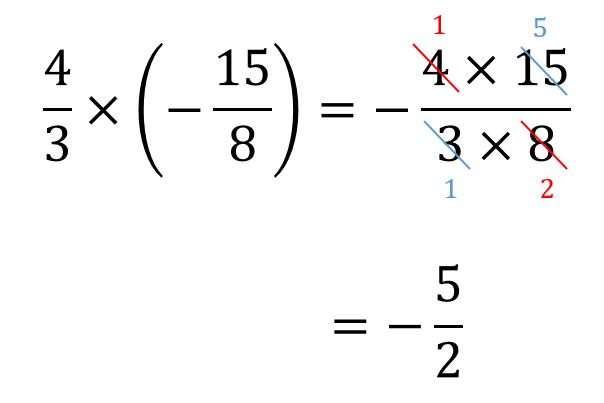
分数のわり算では、逆数にして掛ける！でしたね。
掛け算にチェンジできたら、あとは先ほどと同じように計算していきましょう。
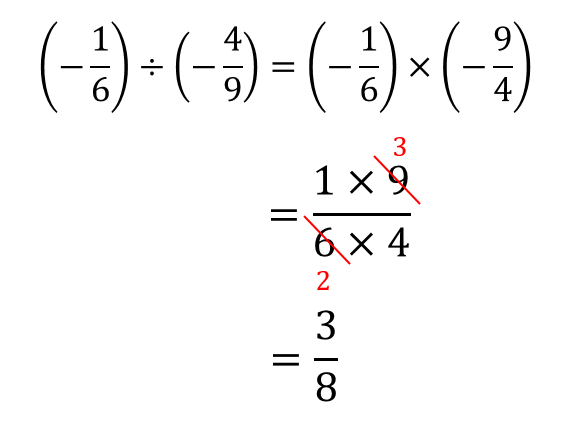
分数の累乗
次は分数の累乗です。
累乗の計算ってなんだっけ？
という方はこちらの記事も参考にしてみてくださいね＾＾
累乗のルールが分かれば、あとは掛け算と一緒ですね＾＾
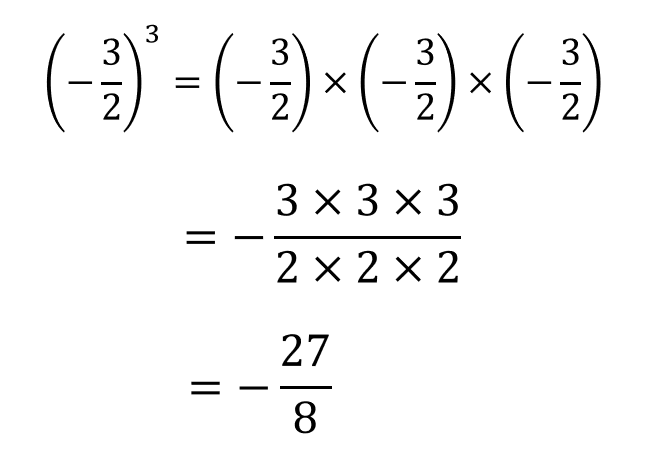
練習問題に挑戦してみよう！
それでは、練習問題を通して理解を深めていきましょう！
次の計算をしなさい。
$$\large{\frac{3}{4}-\left(\frac{7}{12}-\frac{2}{3}\right)}$$
次の計算をしなさい。
$$\large{\left(-\frac{3}{2}\right)^2\div \frac{27}{8}}$$
次の計算をしなさい。
$$\large{\frac{2}{3}-\frac{7}{10}\div \left(-\frac{7}{15}\right)}$$
まとめ
お疲れ様でした！
分数の計算は、見た目が難しそうに見えるので避けられがちですが、しっかりとやり方を確認すればそんなに難しいものではありませんでしたね＾＾
やり方が分かったら、あとは演習あるのみです！
徹底的に問題演習をして、完璧にしていきましょう。
ファイトだー(/・ω・)/
- 正負の数とは？
- 絶対値とは？
- 大小関係を不等号で表すためのポイント
- 加法・減法をマスターしよう！
- 乗法・除法をマスターしよう！
- 累乗の計算とは
- 正負の数、分数計算のやり方を問題解説！ ←今回の記事
- 正負の数の利用、平均を使った問題を解説！
- 正負の数の問題まとめ！計算のやり方を確認しよう！
★上級者向け★
数スタがあなただけの先生になります！
学校、塾の宿題 入試の過去問 など
自分だけで解くのが難しい問題があれば、
一緒に解決しましょう！
数スタの質問対応サービス
詳しく内容はこちらから！
数スタのメルマガ会員さんは、こちらの
質問対応サービスが無料で利用できる！？
数スタの無料メルマガでは、
毎回のメルマガで配布されるポイントを使って、
- ZOOMを使ったオンライン個別指導
- チャットを使った質問対応
- 入試問題の詳しい解説教材
などが無料で手に入ります！
がんばって成績を上げたい方は、ぜひ登録してくださいね！
