【中1数学】正負の数の問題まとめ！計算のやり方を確認しよう！

今回の記事では、中1数学で学習する

「正負の数の問題」

について、解き方や考え方をまとめておきます。

 

【中1数学】正負の数の加法・減法

正負の数の加法・減法では、かっこを外すということがポイントでしたね！

$$\begin{eqnarray}(-2)+(-4)&=&-2-4\\[5pt]&=&-(2+4)\\[5pt]&=&-6 \end{eqnarray}$$

$$\begin{eqnarray}(-5)-(-8)&=&-5+8\\[5pt]&=&+(8-5)\\[5pt]&=&3 \end{eqnarray}$$

 

かっこのはずし方、その後の計算方法について詳しく確認したい場合は

>【正負の数】計算の仕方（コツ）加法・減法をマスターしよう！

こちらの記事をご参考ください。

 

【中1数学】正負の数の乗法・除法

正負の数の乗法、除法では符号の決め方がポイントでしたね。

計算する数の中に

マイナスが奇数個（1,3,5…）あるときには答えはマイナス

マイナスが偶数個（2,4,6…）あるときには答えはプラス

となります。

$$\begin{eqnarray}(-2)\times 3&=&-(2\times 3)=-6 \end{eqnarray}$$

$$(-4)\div (-2) =+(4\div 2)=2$$

 

もっと複雑な乗法、除法の計算については

>【正負の数】乗法と除法の計算方法（コツ）をマスターしよう！

こちらの記事をご参考ください。

 

【中1数学】正負の数の累乗

累乗の計算で気を付けたいのは符号です。

$$3^2=3\times 3=9$$

これは、3を2回掛けましょう。ということなので上のような式になります。

 

$$(-3)^2=(-3)\times (-3)=9$$

これは、\((-3)\)を2回掛けましょう。ということなので上のような式になります。

 

一方で、こちらの計算は注意が必要。

$$-3^2=-(3\times 3)=-9$$

マイナスは置いといて、3の部分だけを2回掛けましょう。ということになります。

 

指数がどこについているのかで、何を何回掛けるのかが変わってくるので注意してくださいね！

分数を含む累乗の計算や100乗は！？といった問題については

>【正負の数】累乗とは？計算方法を丁寧に解説します！

こちらの記事をご参考ください。

 

【中1数学】正負の数の大小

それぞれの大小関係を考える場合には、数直線をイメージしてみるといいですね。

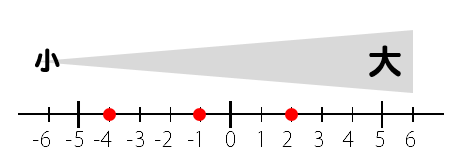
数直線の左にあれば小さい、右にあれば大きいということが分かります。

よって、それぞれの数の大小関係は

$$-4<-1<2$$

と表すことができます。

3つ以上の数の大小関係を表すときには

$$小<中<大$$

のように数字を並べ替えて表すようにしましょう。

 

分数などの大小関係を比べるときについては

>【正負の数】大小関係を不等号で表すためのポイントまとめ

こちらの記事で詳しく解説しています。

【中1数学】正負の数の利用

 

それぞれの曜日での貸し出し冊数を求めると

【月曜】\(100+3=103冊\)

【火曜】\(100-2=98冊\)

【水曜】\(100+12=112冊\)

【木曜】\(100-7=93冊\)

【金曜】\(100+9=109冊\)

これを使って平均を計算すると

$$平均=\frac{103+98+112+93+109}{5}=103冊$$

 

または、それぞれの基準との差の平均を求めることで次のように求めることもできます。

$$基準との差の平均=\frac{(+3)+(-2)+(+12)+(-7)+(+9)}{5}=3$$

$$平均=100+3=103冊$$

 

【中1数学】正負の数のまとめ

正負の数の単元では、正確に計算ができるように練習をしておきましょう。

もっと発展的な計算練習をしたい方は

>【中1数学】正負の数、分数計算のやり方を問題解説！

>【高校入試】正負の数の難問を解説！難関高校の入試問題に挑戦しよう！

こちらで難しい計算問題についても解説しているのでご参考ください。