【正負の数】計算の仕方（コツ）加法・減法をマスターしよう！

今回は正負の数の

加法（足し算）・減法（引き算）

の計算方法を丁寧に説明していきます。

中学に入ってすぐに学習する単元なんだけど

数学の基礎中の基礎と言ってもいい部分だから

しっかりと理解しておきたいね！

今回学習する正負の数の計算を

ちゃんとできるようにしておかないと

他の単元でも苦労することになっちゃうから

気合を入れて頑張っていきましょう！

数学がどうも苦手だ…

っていう2年生や3年生のみんなも

今回はしっかりと復習していってください＾＾

今回の記事内容について、こちらの動画でまとめています！

正負の数の加法・減法　計算のコツ

正負の数の加法・減法ではいろんなパターンがある。

まずは

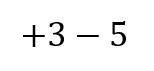
このように式にかっこがついていなくてシンプルなやつ

次は

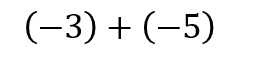
こんな感じで数字にかっこがついていて

少し複雑そうに見えるやつ

更には

こんな…

見るのも嫌になってしまいそうな複雑なやつ

それでは順に解き方を確認していきましょう。

かっこがないパターンの解き方

まずは、かっこが付いていない計算問題から挑戦してみよう。

これらの計算を解いていくためには

こんな考え方をしていくといいよ！

数直線を使った考え

数直線を使って加法・減法を考えてみましょう。

ちなみに数直線っていうのは

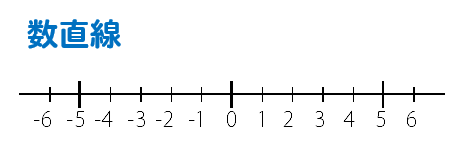
こういう目盛りのある直線のこと

とっても便利だから

この数直線を使って考えてみよう。

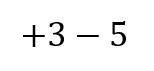
この計算を数直線を使って計算してみよう。

＋（プラス）の数であれば進む

ー（マイナス）の数であれば戻る

というようにすごろくのようなイメージで考えてみる。

スタート地点は、数直線の０（原点）のところ

まずは＋３なので原点を出発して３つ進みます。

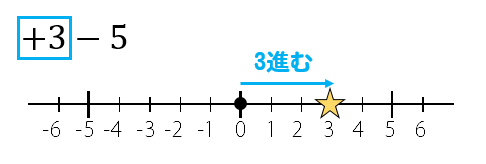
すると３の場所に移動しました。

次は－５なので３の場所から５つ戻ります。

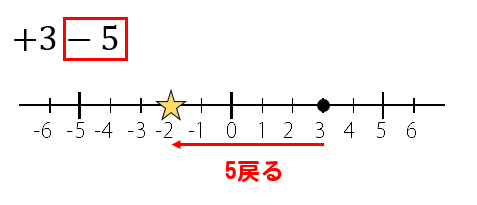
するとー２の場所に移動しました。

よって

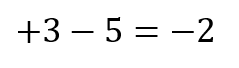
原点から３つ進んで5つ戻って

答えはー２

ということが分かります。

これが数直線を使った

正負の数の加法・減法の考え方です。

＋なら進んで

ーなら戻る

最終的に止まった場所が答え

シンプルですね！

他にも計算してみましょう。

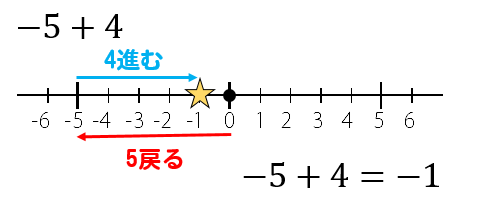
－５と＋４だから

原点から５つ戻って、４つ進む

答えはー１ですね

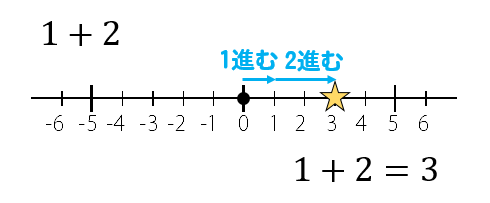
１と＋２だから

原点から１つ進んで、更に2つ進む

答えは３ですね

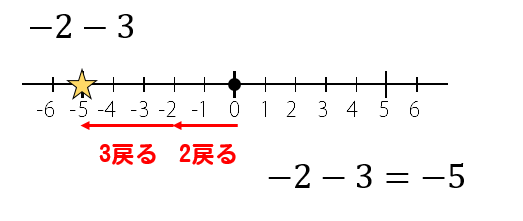
－２とー３だから

原点から２つ戻って、更に3つ戻って

答えはー５ですね。

このように数直線を使って考えてみると

正負の数の加法・減法は考えやすくなるのではないでしょうか。

発展的な考え方

数直線を使えば、余裕だぜっ！

って思ってもらえましたか？

確かに数直線を使った考え方って

とっても便利なんですが

限界もあります。

それは…

計算せよっ！

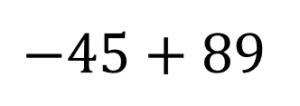
どーーーん！！

ー４５だから

４５戻って…

次は８９だから

８９進んで…

って数が大きすぎて数直線ムリーーー！！

ってなっちゃいますよね。

数直線の考え方は

正負の数入門者には良いのですが

計算に慣れてきた中級者には

少し物足りなく感じてしまいます。

という訳で

次は、こういった大きな数が出てきても

計算できるようになる為の

少し発展的な考え方もお伝えします。

まずはこちらを見てみましょう。

これらのように

進む、進む

戻る、戻る

のように同じ方向に移動する計算の場合

このように計算することができます。

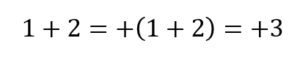
詳しく見てみるとこんな感じです。

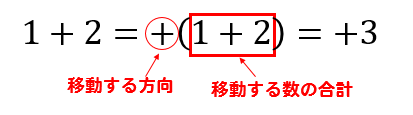
１と＋２は両方とも進む数だから

移動する方向は＋

進む数の合計は１＋２＝３だから

答えは＋３

（もちろんプラスは省略して３でもOK）

－３とー２は両方とも戻る数だから

移動する方向はー

戻る数の合計は３＋２＝５だから

答えはー５

両方の数が同じ方向に移動する場合には

このように計算すると

数直線を書かなくても計算ができるようになるね。

そうすると、こんな大きな数の計算でも…

簡単にできるようになったね！

次は移動する方向が違う計算も見てみよう。

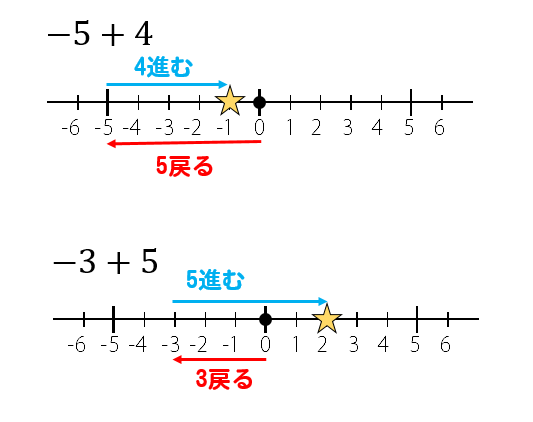
これらのように

進む、戻る

といったように移動する方向が違う場合には

このように計算することができます。

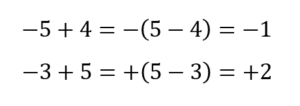
詳しく見てみるとこんな感じです。

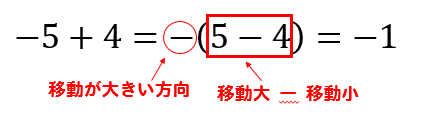
－５と＋４なので

５つ戻って、４つ進むことになるのですが

戻る方と進む方

どちらの移動が大きいかというと

戻る方ですね

だから符号はーとします。

そして、移動が大きい５と移動が小さい４の差を求めると

５－４＝１となります。

よって、答えはー１

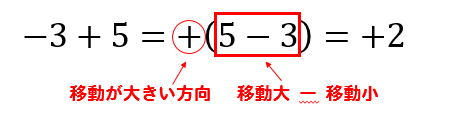
－３と＋５なので

３つ戻って５つ進むことになるのですが

進む方が移動が大きいですね

だから、符号は＋とします。

そして、移動が大きい５と移動が小さい３の差を考えると

５－３＝２となります。

よって、答えは＋２（もちろん２でもOK）

進むと戻るが混ざっている計算の場合には

どちらに大きく動いているかを判断して

計算をしていくようになります。

最初は難しく感じますが、慣れてくると

こんな大きな数でも簡単に計算できるようになります。

かっこがあるパターンの解き方

それでは、次はかっこのついている計算を考えてみよう。

これらの問題を解くためには

まず、かっこのはずし方

というものをマスターしておく必要があります。

かっこのはずし方

例を見てみましょう。

＋（＋５）＝＋５

＋（－５）＝－５

－（＋５）＝－５

－（－５）＝＋５

こんな感じでかっこを外すことができます。

なんで？？って思われるかもしれませんが

＋の数を貯金

ーの数を借金だと思って

それぞれイメージしてみましょう…

＋（＋５）

これは貯金５が増えるということを表しています。

ってことは単純に考えて

お金が増えるから＋５と同じ意味になるね

＋（＋５）＝＋５

次に

＋（－５）

これは借金５が増えるってことを表しています。

ってことは

借金が増えてるってことなんで

お金は減ってるって考えることができるよね

だから、単純に－５と同じってこと

＋（－５）＝－５

ー（＋５）

これは貯金５が減ったって考えます。

お金は減っているのでー５と同じ。

ー（＋５）＝ー５

ー（－５）

これは借金５が減った

つまり、その人にとっては

お金が増えたと同じ意味になります。

だから、＋５になるわけですね。

ー（－５）

こういうイメージを持っててもらうと

かっこをはずしたときの

なんで？？

が理解してもらえるかな。

かっこがついた式の計算手順

それでは、かっこがついた計算をやってみましょう。

かっこがついていると複雑に見えちゃうので

まずは、かっこをはずしてやります。

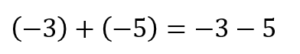
（－３）はかっこの前が＋なのでそのままー３

＋（－５）はかっこの前が＋なのでそのままー５　となります。

かっこがはずせたら

上で練習してきたように

計算すればOKです！

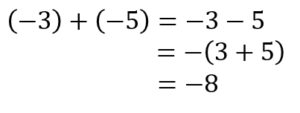
他も同様に計算してみましょう。

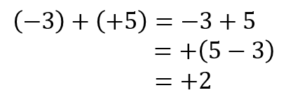
（－３）はかっこの前が＋だからそのままー３

＋（＋５）はかっこの前が＋だからそのまま＋５　ですね。

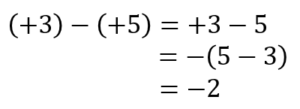
（＋３）はかっこの前が＋だからそのまま＋３

ー（＋５）はかっこの前がーだから符号を変えてー５　ですね。

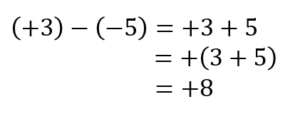
（＋３）はかっこの前が＋だからそのまま＋３

ー（－５）はかっこの前がーだから符号を変えて＋５　ですね。

このようにかっこのはずし方を覚えてしまえば

計算自体は今まで通り考えることができるよ。

複雑な計算の解き方

それでは、最後に

一番複雑そうに見えた

この計算に挑戦してみましょう。

まずは上でやってきたのと同じように

かっこをはずしてやります。

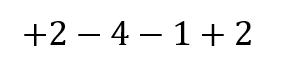
するとこんな式になりますね。

これを詳しく見てみると

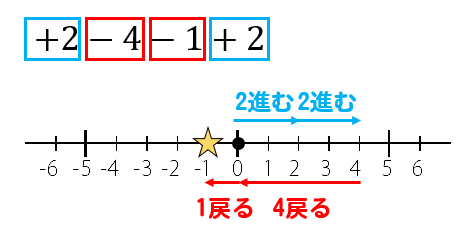
移動回数が多いだけで

やっていること自体は今までと同じです。

ただ、こういう移動回数が多い計算をやる場合は

なるべく同じ方向に移動するもの同士を

最初に計算してしまうと楽です。

つまり、今回の場合は

＋２＋２＝＋４

合計４つ進む

－４－１＝－５

合計５つ戻る

だから

＋４－５＝－（５－４）＝－１

このように計算していくのがおススメです。

【特典】保護者さん、学生さん用の追加教材を用意しました！

お疲れ様でした＾＾

ここまでのところで加法、減法のルールは理解してもらえましたか？

やり方がわかったら、あとは問題を解きまくってスラスラできるように仕上げておきたいです！

というわけで、最後まで取り組んでくれたお礼として、理解を深めるための追加演習をプレゼントします。

今回用意した追加課題

• 正負の加減を身につける練習問題＆動画解説
• 理解を深める演習プリント2枚（基礎編）
• 計算力を高める2けたの計算プリント2枚（チャレンジ編）

---

今回の課題をお子さんと一緒に取り組んでいただくことで、次のようなメリットがあります！

お休みの日などを利用して、ぜひ家庭学習にご活用ください＾＾

• 反射的にスラスラ解ける計算力が身につくので、授業の理解度が高まり中学のスタートダッシュが切れる！
• 計算スピードが向上！学校の宿題が一瞬で終わっちゃうので家庭学習がスムーズに！
• 参考書を買ったり、塾に行かなくても正負の加減はこれだけでバッチリ仕上がる！

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます。

正負の加減は中学数学の土台となるものすごく大事な内容です。

ここを完璧に仕上げておくことで今後の学習がスムーズになってくるので、今のうちにがんばってやっておきましょう(‘ω’)ノ

というわけで、今すぐチャレンジしてみよう！

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定です。

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

加法・減法のまとめ

かっこがついてない計算の場合

• 慣れるまでは数直線を使って、すごろくのように考えよう
• 慣れてきたら発展的な求め方ができるようにしておこう

かっこがついている計算の場合

• まずはかっこをはずして、式をシンプルにする
• かっこがはずせたら、かっこなしと同様に計算しよう

複雑な計算の場合

• まずはかっこをはずして式をシンプルにする
• 同じ方向に移動するもの同士を初めに計算してあげるとラクになるよ