【中1数学】絶対値とは？問題の解き方をイチから解説！

今回は中1数学で学習する

「絶対値とは」

について解説していきます。

簡単な内容なので、

この記事を通してサクッと理解していきましょうね！

絶対値とは

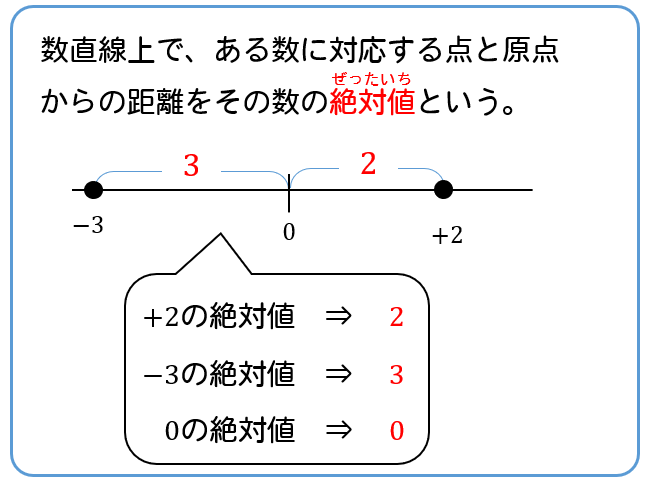
絶対値とは、原点からの距離のことをいいます。

\(+3\)であれば、原点から右に\(3\)離れているので、絶対値は\(3\)。

\(-5\)であれば、原点から左に\(5\)離れているので、絶対値は\(5\)。

となります。簡単ですね(^^)

絶対値とは距離を表した値なので、負の数が答えになることはありません。

必ず0以上になります。

なので、絶対値を答えるときには、その数の符号を取った値。

と覚えておいてもOKですね！

では、例題を通して絶対値の問題の解き方を身につけておきましょう。

絶対値とは原点からの距離であり、符号をとった値と等しくなります。

したがって、答えは

（1）\(+3\)　⇒　\(3\)

（2）\(-2.1\)　⇒　\(2.1\)

（3）\(+\frac{2}{5}\)　⇒　\(\frac{2}{5}\)

となります。

こちらの問題は先ほどとはちょっと聞かれ方が違いますね。

「絶対値が\(2\)になる数」＝「原点からの距離が\(2\)になる数」

原点から右側に2離れている点 \(2\)

原点から左側に離れている点 \(-2\)

このように \(2,-2\) の2つであることが分かります。

絶対値が2以下となるのは、

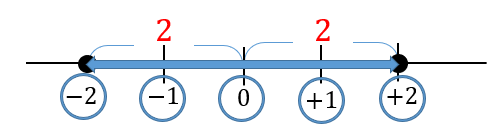
このような範囲になります。（原点に近い範囲）

「以下」ということは、\(-2,+2\)も含まれることになります。

この点に気を付けて答えを書き出すと

$$-2,-1,0,1,2$$

となります。

ここでは「以上・以下」「より大きい・小さい、未満」といった言葉の違いが重要になります。

絶対値【練習問題】

まとめ！

絶対値とは原点からの距離！

これを覚えておけば簡単な内容ですね(^^)

この絶対値は、次に学習する「数の大小」「正負の加減」でも役に立つものです。

なので、今回の内容に不安がある方は練習問題を何度も解いて、しっかりと理解を深めておいてくださいね！