【正負の数】乗法と除法の計算方法（コツ）をマスターしよう！

今回の記事では

正負の数の

乗法（掛け算）除法（割り算）

の計算方法について考えてみよう！

加法・減法の計算のコツについては

こちらで解説しているので参考にしてみてください＾＾

【正負の数】計算の仕方（コツ）加法・減法をマスターしよう！

今回の記事内容について、こちらの動画でまとめています！

正負の数の乗除　計算のコツ

正負の数の乗法・除法は

加法・減法に比べると

とっても簡単です！

では、こちらの掛け算を例に考えてみましょう。

（＋５）×（－２）

計算手順としては

1. 答えの符号を決める
2. 数を計算する

以上！

たったこれだけです。

まず、１の「答えの符号を決める」というのは

どういうことかと言うと

正負の数の乗法・除法は

計算する数の中に

いくつ負の数（ー）が含まれているかで

答えの符号が決まるという性質があります。

まとめておくとこんな感じです。

つまり

（＋５）×（－２）

この場合、負の数はー２の１個だけなので

負の数が奇数個

答えの符号はマイナスとなります。

（＋５）×（－２）＝－〇

これで答えの符号が決まりました。

次は手順２の「数を計算する」です。

これは至ってシンプルです。

ただただ数を計算するだけ

＋５の５

－２の２

それぞれの符号を取っ払った数を計算します。

５×２＝１０

これで答えの数も決定したので

手順１と手順２を組み合わせて

（＋５）×（－２）＝－１０

となります。

除法も例を見ながら考えてみましょう。

（－１０）÷（－２）

こちらも手順は同じです。

まず符号を決めます。

今回は負の数が２つあるので

負の数が偶数個の場合、答えの符号はプラスとなります。

数の計算は

１０÷２＝５　となるので

以上を組み合わせると

（－１０）÷（－２）＝５

となります。

乗法・除法の基本は以上ですが

実際の計算問題ではいろいろな状況が考えられます。

以下では実際の問題を考えながら

様々な状況での計算方法をお伝えしていきます。

問題に挑戦してみよう！

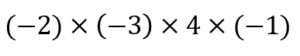
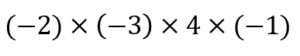
うわー数がいっぱいある…って感じですが

基本に忠実に

手順通りいきましょう！

まず手順１答えの符号を決めましょう。

負の数はー２とー３とー１の３個

負の数が奇数個なので答えはマイナス

次は手順２の数を計算

それぞれの符号を取っ払った数を計算します。

２×３×４×１＝２４

よって、手順１と２より

答えは

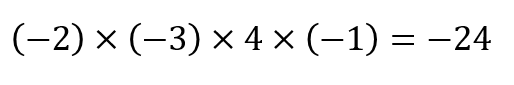
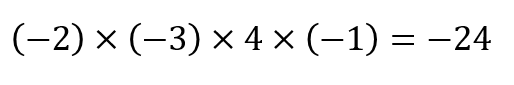
しっかりと手順を踏めば大丈夫です！

何回も計算練習すれば

スピードも正確性もアップするので

慣れるまでは反復練習を！

次！

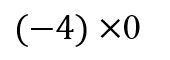
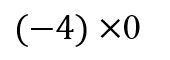
見た目はすっごくシンプルですね

ただ、ちょっとだけ注意が…

負の数が１個なので答えの符号をマイナスと

してしまいたくなるところですが

数の計算をすると

４×０＝０となります。

０は正でも負でもない数なので

プラスやマイナスはつけません。

よって、答えは

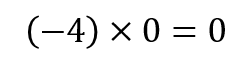
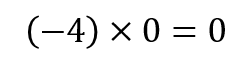
答えに０が出てきたときには

間違って符号をつけないよう

気を付けてくださいね！

次！

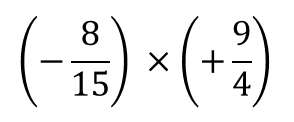
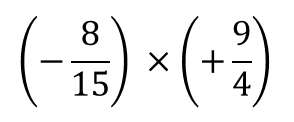
出ました分数！

これも手順通り考えてみましょう。

まず、負の数が１個なので

答えの符号はマイナス。

次は数の計算です。

分数の掛け算はこのように約分できるところがあれば

先に約分してから計算してやりましょう。

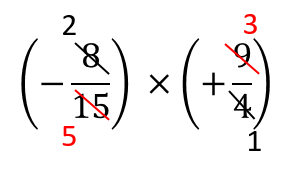
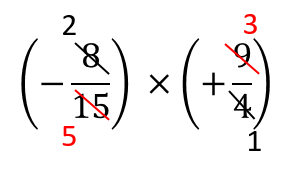
よって、答えは

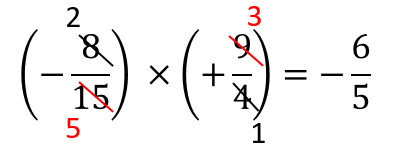
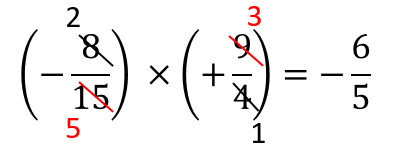
丁寧に約分してやることが大事ですね。

次！

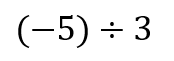
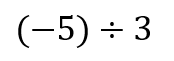
おっと、ここにきて簡単そうな問題！

と思いきや…

符号はすぐにマイナスって分かるんだけど

数の計算が

５÷３＝１.６６６６６…

割り切れないっ！！

これだと答えが出せないので困ってしまう。

そんなときには

逆数を使って乗り切ろう！

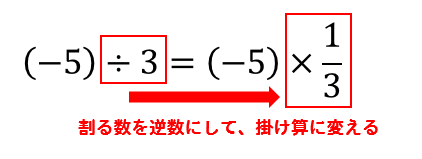
割り算の場合

割る数を逆数にして、掛け算に変えても

出てくる答えは同じという性質があります。

なので

数が割り切れない！という場合には

この方法を用いて、分数として答えを出してやりましょう。

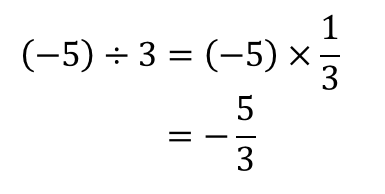
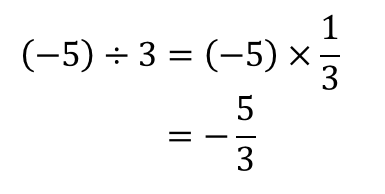
ついでにこれも！

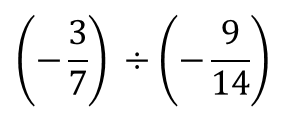
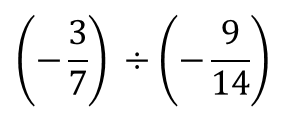
今度は分数同士の割り算です。

答えの符号はプラスですね。

これも上の問題同様

このままだと数の計算がややこしいので

割る数を逆数にして、掛け算に変えてしまいます。

割り算を掛け算に変えてしまえば

あとは、約分して

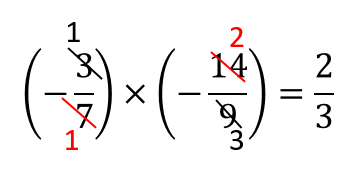
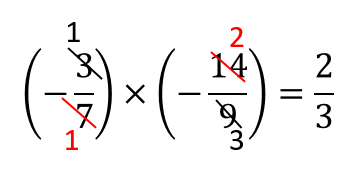
以上、問題演習でした。

お疲れ様でした！

いろんなシチュエーションがあったかと思いますが

やはり基本が大切でしたね。

【特典】最後まで取り組んでくれた方への追加教材！

お疲れ様でした＾＾

ここまでのところで乗法・除法のルールは理解してもらえましたか？

符号の決め方がちゃんとわかっていれば簡単に解くことができますね＾＾

あとは問題を解きまくってスラスラできるように仕上げておきたいです！

というわけで、最後まで取り組んでくれたお礼として、理解を深めるための追加演習をプレゼントします。

今回用意した追加課題

• 正負乗除のポイント＆演習をまとめたプリント

---

今回の課題をお子さんと一緒に取り組んでいただくことで、次のようなメリットがあります！

お休みの日などを利用して、ぜひ家庭学習にご活用ください＾＾

• 反射的にスラスラ解ける計算力が身につくので、授業の理解度が高まり中学のスタートダッシュが切れる！
• 計算ルールが身につくので、学校のワークなどの宿題をお子さんが1人でスラスラ解けるようになる
• やり終えたプリントをノートに貼っておけば、いつでも簡単に復習ができるのでテストまで記憶がバッチリ定着！
• 10分で取り組めるので、習い事の合間などスキマ時間を使って勉強できる
• 参考書を買ったり、塾に行かなくても正負の加減はこれだけでバッチリ仕上がる！

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます。

乗法・除法の符号の決め方はものすごく重要！

今後の単元でも必須となる知識なので今のうちにしっかりと固めておきましょう！

というわけで、今すぐチャレンジしてみよう！

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定です。

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

正負の数　乗除まとめ

正負の数の乗法・除法は

• 符号を決めること
• 数の計算をすること

この２点に尽きます。

符号の決め方は

• 負の数が奇数個ならマイナス
• 負の数が偶数個ならプラス

数の計算をする部分では

• ０が出てきたときには符号をつけない
• 割り算で割り切れないときには、分数の形で表す
• 分数同士の割り算は逆数を使って、掛け算として計算する

などのポイントがありました。

あとは、問題演習を繰り返しながら

計算方法を正確に身につけていきましょう。