今回は、中2で学習する『連立方程式』の単元から食塩水の濃度に関する文章問題の解き方について解説していくよ!
濃度って聞くと…
なんかイヤ!
っていう人も多いのではないでしょうか(^^;
でもね、解き方を知っちゃうと
え、こんなに簡単でいいの?

という、ラッキー問題であることに気が付くはずです。
今回は、そんな食塩水の問題についてマスターしていこう!
挑戦する問題はこちらです。
問題
5%の食塩水と8%の食塩水を混ぜて、6%の食塩水を300gつくりたい。2種類の食塩水をそれぞれ何gずつ混ぜればよいか求めなさい。
今回の問題はこちらの動画内でも解説しています!
動画を見ればサクッと理解できると思うのでぜひご活用ください^^
[スタセミ中2バナー]
食塩の量を求める方法
濃度の問題では、食塩水の中にどれだけ塩が含まれているか。
これを計算することが重要なポイントとなります。
例えばね
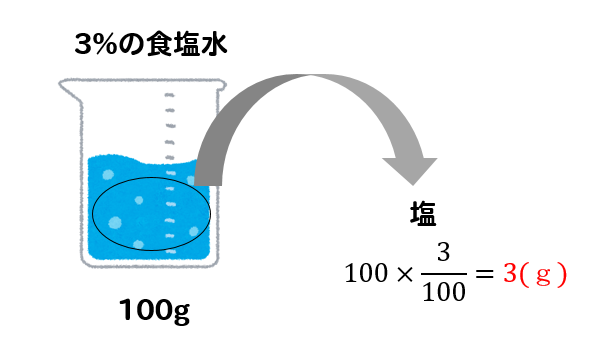
こんな感じで計算することができますね(^^)

パーセントの計算を忘れてしまった方は、こちらの記事で復習しておきましょう。
文字が出てきても同じように求めることができますね。
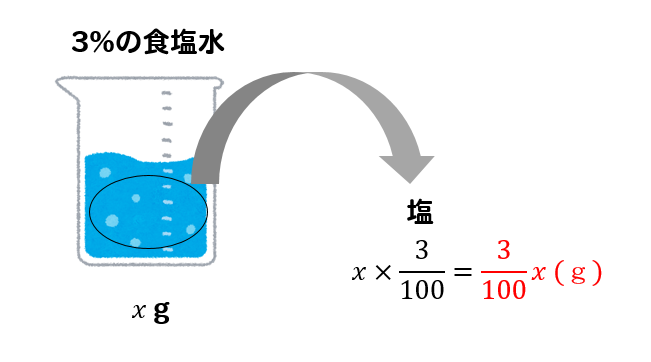
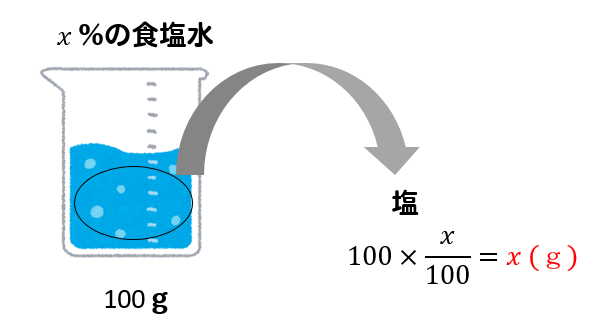
それでは、食塩の量を計算する方法を頭に入れておいて問題を見ていきましょう。
濃度問題 式の作り方
問題
5%の食塩水と8%の食塩水を混ぜて、6%の食塩水を300gつくりたい。2種類の食塩水をそれぞれ何gずつ混ぜればよいか求めなさい。
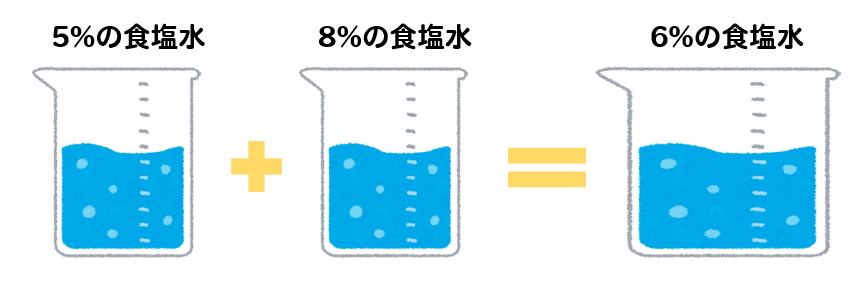
5%の食塩水を\(x\) g、8%の食塩水を\(y\) gとすると1つ式ができあがります。
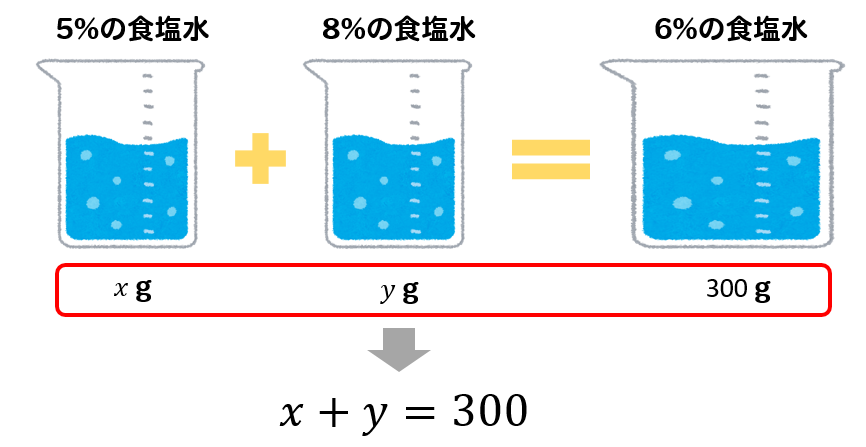
次は、それぞれの食塩水に含まれる塩の量に注目していきます。
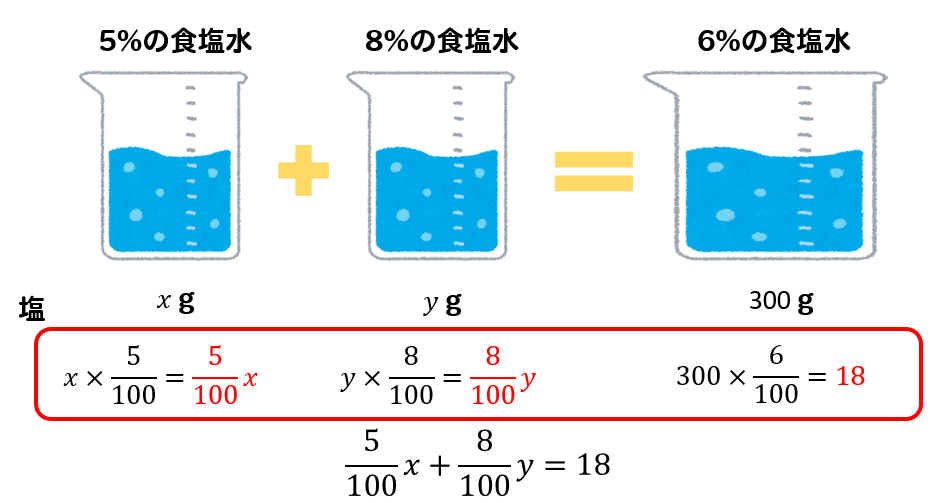
2つの食塩水を混ぜ合わせるということは、その中に含まれている塩の量も合計されるということです。
だから、このような式ができあがります!
約分ができるのですが、方程式を解いていく上で分母を消していきます。
今のところは約分せずにこのままでOKです。
これで連立方程式の完成です!
$$\displaystyle{\begin{eqnarray} \left\{ \begin{array}{l} x + y = 300 \\ \frac{5}{100}x + \frac{8}{100}y = 18 \end{array} \right. \end{eqnarray}}$$
あとは、この連立方程式を解いていきましょう。
まずは、分数を含む式の両辺に100をかけて分母を消してやります。
$$\frac{5}{100}x\times 100 + \frac{8}{100}y\times 100 = 18\times 100$$
$$5x+8y=1800$$
するとシンプルな式ができあがります。
\begin{eqnarray} \left\{ \begin{array}{l} x + y = 300 \\ 5x+8y=1800 \end{array} \right. \end{eqnarray}
あとは、この連立方程式を解けば完成です。
答えは
$$x=200, y=100$$
となります。
よって、5%の食塩水は200gで8%の食塩水は100g混ぜれば良いということになります。
食塩水の文章問題はいたってシンプルです!
- 食塩水の量の和で式を作る。
- 塩の量の和で式を作る。
- 解く。
以上!
多くの人が塩の量を表すことができず苦労しているようです。
パーセントの使い方を知ってしまえば簡単なことですよね(^^)
それでは、練習問題に挑戦して理解を深めていきましょう。

練習問題で理解を深める!
問題
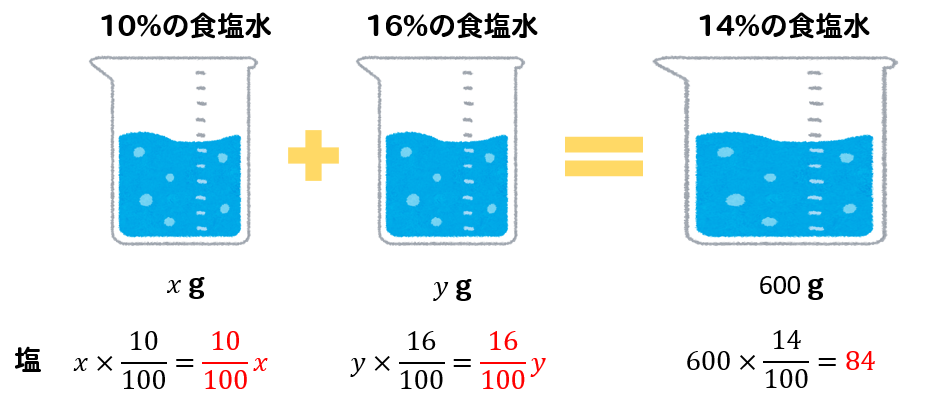
10%の食塩水と16%の食塩水がある。これらを混ぜて14%の食塩水600gをつくった。それぞれ何gずつ混ぜたか求めなさい。
濃度を求める応用編!
問題
2種類の食塩水A、Bがある。Aを50g、Bを100g混ぜると12%の食塩水ができ、Aを200gとBを160gを混ぜると14%の食塩水ができるとき、AとBの食塩水の濃度を求めなさい。
このように食塩水の量ではなく、濃度の方を問われる問題もあります。
こちらの文章問題も解説しておきますね!
流れは先ほどの問題と一緒です。
食塩水Aの濃度を\(x\)%、食塩水Bの濃度を\(y\)%として
食塩の量に注目していきましょう。
Aを50g、Bを100g混ぜ合わせたときを考えると
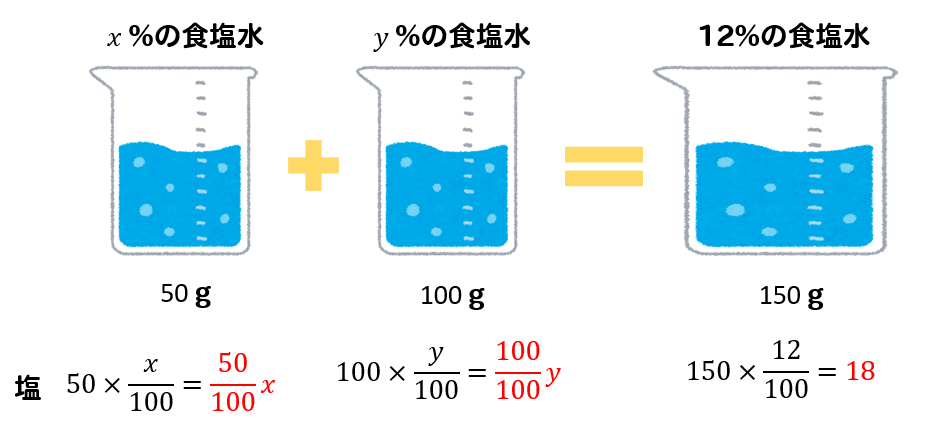
$$\frac{50}{100}x+\frac{100}{100}y=18$$
という式ができあがります。
両辺に100を掛けて、シンプルな式に変形しておきましょうか。
$$50x+100y=1800$$
あ、さらに10で割ってやるともう少しシンプルにできそうですね。
$$5x+10y=180$$
次にAを200g、Bを160g混ぜ合わせたときを考えると
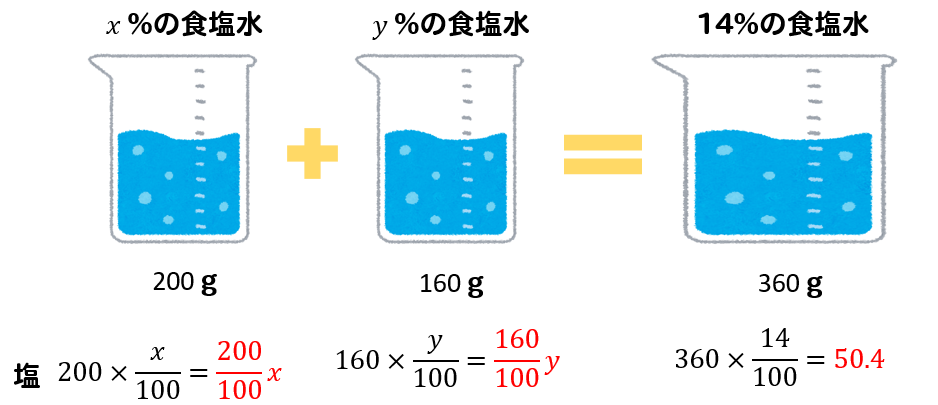
$$\frac{200}{100}x+\frac{160}{100}y=50.4$$
という式ができあがります。
式を変形してシンプルな形にすると
$$20x+16y=504$$
となります。
これで2つ式ができたことになるので
\begin{eqnarray} \left\{ \begin{array}{l} 5x+10y=180 \\ 20x+16y=504 \end{array} \right. \end{eqnarray}
この連立方程式を解いていけば完成です。
答えは
$$x=18, y=9$$
となります。
よって、Aの食塩水は18%でBの食塩水は9%となります。
濃度の文章問題まとめ
お疲れ様でした!
濃度の文章問題って難しそうに見えますが
ちゃんと%のルールを覚えていれば簡単ですね(^^)
まぁ、簡単とは言っても
どうしても分数や小数などの数値が出てきてしまいます。
連立方程式の計算が苦手な方は、まずは計算練習をこなして基礎学力をつけていくことをおススメします。
【連立方程式】加減法、代入法の簡単な練習問題!これでテストはバッチリ!















すげー
ガチで助かった
ありがとう!!
わかりやすいです⁉
いつもありがとうございます
ありがとうございます^^
助かりました。
ありがとうございます
すごくわかりやすかったです
ついでに2元1次方程式までわかりました!
本当にありがとうございます
GOOD!!
めちゃくちゃわかりやすい
とても分かりやすいし、面白いです!!
もっと難しいのもあって欲しいです(!?)
ありがとうございます!
もっと難しいものも用意しようかな