今回は数学Bで学習する『ベクトル』の単元から、単位ベクトルに関する問題を解説していくよ!
そもそも単位ベクトルってなに!?
名前からして、なんだか難しそうなんだけど…
ということで、単位ベクトルはこの単元の中でも質問が多い用語であります。
それでは、1つずつ解説していきますね(^^)
単位ベクトルとは?
大きさ(長さ)が1であるベクトルのことを単位ベクトルといいます。
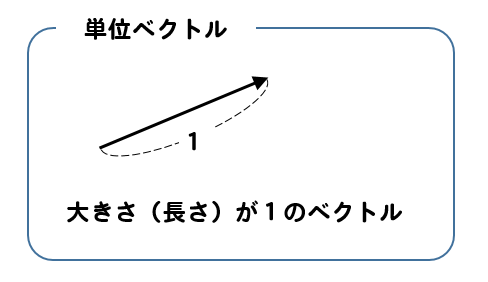
とにかく!
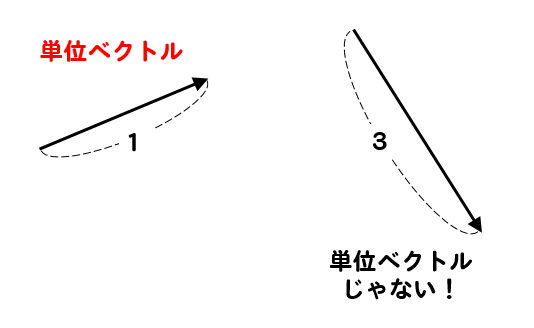
長さが1になっているベクトルのことを単位ベクトルっていうよ。
別に難しいことはありませんね(^^)
単位ベクトルの求め方
次に、例題を使って単位ベクトルの求め方を確認していきましょう。
例題
\(\vec{a}=(1,2)\)と同じ向きの単位ベクトルを求めなさい。
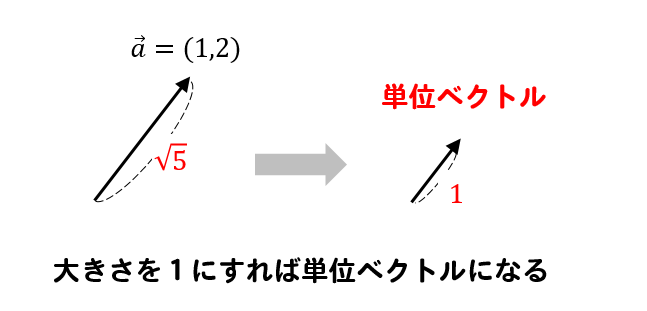
\(\vec{a}\)について、詳しく見ていくと

大きさが\(\sqrt{5}\)のベクトルであることが分かりますね。
大きさが1ではないので、これは単位ベクトルとは言えません。
このベクトルの長さを縮めて、大きさを1にしてやると単位ベクトルが完成します。
それでは、どのように大きさを1にすればよいのか?
それは、すごく簡単なことです。
自身の大きさで割ってやればOK!
例えば、大きさが3のベクトルを大きさ1にしようと思ったら
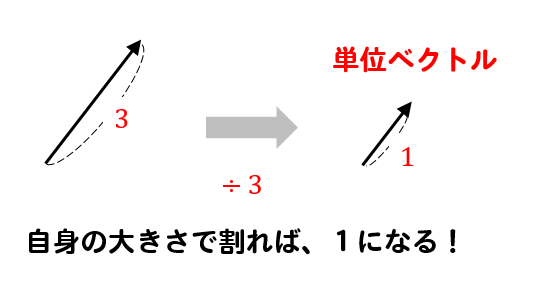
このように3で割ればOKということです。
当然だよね!
$$3\div 3=1$$
同じ数で割ってやれば、1になるはずです。
だから、今回の例題では\(\vec{a}\)の大きさは\(\sqrt{5}\)でしたから
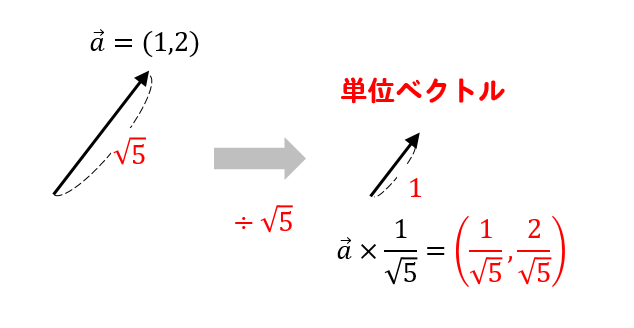
\(\vec{a}\)を\(\sqrt{5}\)で割ってやると単位ベクトルは…
$$\vec{a}\times \frac{1}{\sqrt{5}}=\left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right)$$
このように求めることができます。
単位ベクトルの求め方をまとめておくと
- ベクトルの大きさを求める
- 自身の大きさで割る
以上!
簡単でしたね(^^)
単位ベクトルとは大きさが1のベクトルであるっていうことを覚えておけば大丈夫です!
公式っぽくまとめておくとこんな感じです。
参考程度にどうぞ
\(\vec{a}\)と同じ向きの単位ベクトルは$$\Large{\frac{\vec{a}}{|\vec{a}|}}$$と表すことができます。
平行な単位ベクトルの求め方
例題
\(\vec{a}=(2,-1)\)に平行な単位ベクトルを求めなさい。
それでは、こちらの例題を使って平行な単位ベクトルの求め方について解説していきます。
基本的には、先ほどやった同じ方向の単位ベクトルを求める方法と同じです。
\(|\vec{a}|=\sqrt{2^2+(-1)^2}=\sqrt{5}\)
であるから、\(\vec{a}\)と同じ方向の単位ベクトルは
$$\frac{\vec{a}}{\sqrt{5}}=\left(\frac{2}{\sqrt{5}}, -\frac{1}{\sqrt{5}} \right)$$
このように求めることができます。
しかし
これで終わりではありません!
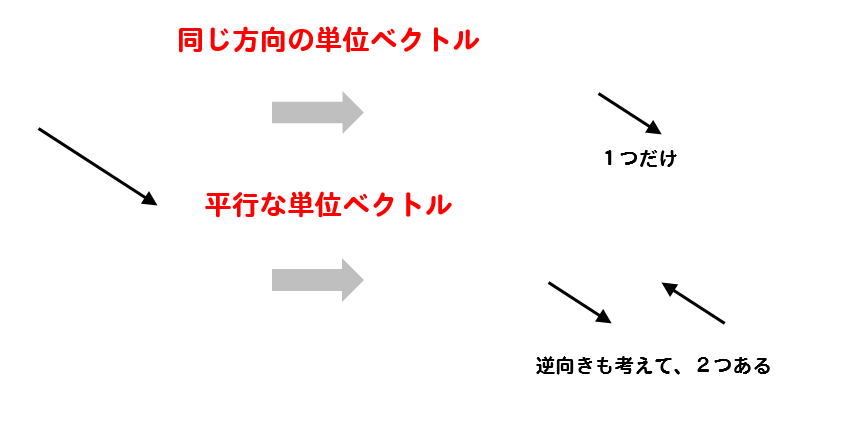
平行な単位ベクトルを求めろ!と言われれば、向きに指定がありません。
よって、逆向きのベクトルも求める必要があります。
つまり
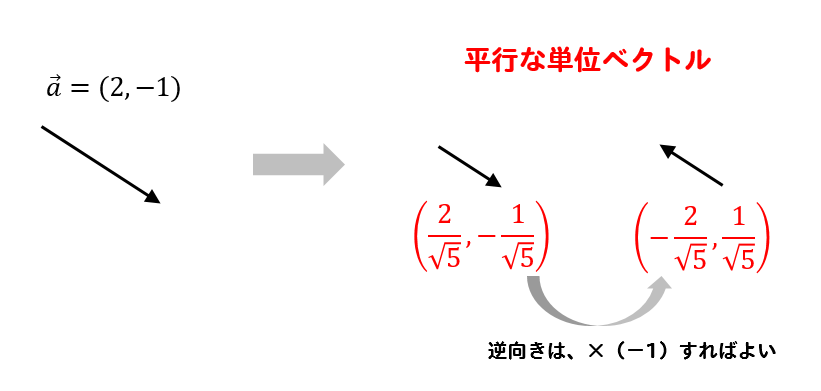
このように2つ求めてあげましょう!
平行な単位ベクトルを求めるポイント!同じ向きの単位ベクトルを求めて、その逆ベクトルを求める。
平行といわれれば、必ず2つ求めることを忘れないように!
数学っぽく式をフルに活用して解く方法についてはこちらで解説しております。
垂直な単位ベクトルの求め方
例題
\(\vec{a}=(2,-1)\)に垂直な単位ベクトルを求めなさい。
求めたい単位ベクトルを\(\vec{b}=(x,y)\)とすると、垂直だから\(\vec{a}\cdot \vec{b}=0\)となりますね。
よって
$$\vec{a}\cdot \vec{b}=2x-y=0$$
更に、\(|\vec{b}|=1\)だから
$$|\vec{b}|=\sqrt{x^2+y^2}=1$$
$$x^2+y^2=1$$
となります。
この2つの式を連立方程式で解くと
\begin{eqnarray} \left\{ \begin{array}{l} 2x – y = 0 \\ x^2 + y^2 = 1 \end{array} \right. \end{eqnarray}
$$(x, y)=\left(\pm \frac{1}{\sqrt{5}}, \pm \frac{2}{\sqrt{5}} \right)$$
となります。
よって、求めたい垂直な単位ベクトルは
$$\left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right), \left(-\frac{1}{\sqrt{5}}, -\frac{2}{\sqrt{5}} \right)$$
まとめ
お疲れ様でした!
単位ベクトルとは、大きさが1のベクトルであり
単位ベクトルを求めるためには自身の大きさで割ることがポイントでした。
更に
同じ方向の単位ベクトルを…
平行な単位ベクトルを…
垂直な単位ベクトルを…
と、いろいろな問われ方をするので、それぞれの解き方をしっかりと身につけておきたいですね(^^)











平行な単位ベクトルをー1掛けてひっくり返して垂直な単位ベクトルにするやり方だと、答えがあってませんよ?
すんません!
該当部分、消しときました!
単位べくと と書かれてるところがありました
ご指摘ありがとうございました!!