高校入試対策演習
小問集合の第4回目です!
目安時間は5分です。
挑戦してみましょう(^^)
第4回 小問集合
(1) \((-2)^3-(-3^2)\times (-4)\) を計算しなさい。
(2)\(x^2-6x\)を因数分解しなさい。
(3)一次関数\(\displaystyle y=-\frac{3}{5}x+3\)のグラフをかきなさない。
(4)男子20人、女子16人のクラスでテストを行ったところ、男子の平均点が\(x\)点で、女子の平均点が\(y\)点であった。このクラスのテストの合計点は何点か、\(x\)と\(y\)を使った式で表しなさい。
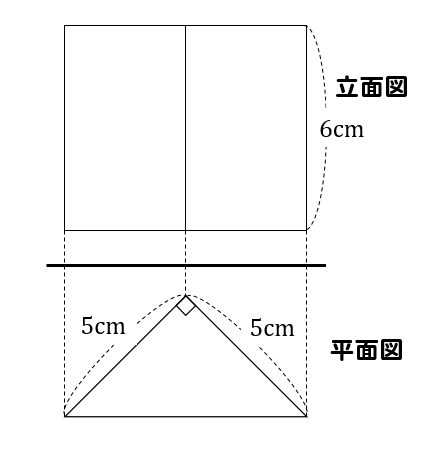
(5)下の図は、三角柱の投影図である。この三角柱の体積を答えなさい。
問題が解けた人は↓で答え合わせをしていきましょう!
ひこ数スタの無料メルマガ講座では、
毎週金曜に、小問演習のプリント&解説動画をお届けしています。
数学の力を伸ばすためには問題演習が欠かせません。
登録は無料ですので、ぜひご活用ください^^
登録直後にこれまでに配信してきた小問課題をまとめてプレゼント。
今すぐ演習にとりかかれますよ!
問題の解答
解答はこちらです。
答え合わせしてみましょう(^^)
答え
(1)\(-44\)
(2)\(x(x-6)\)
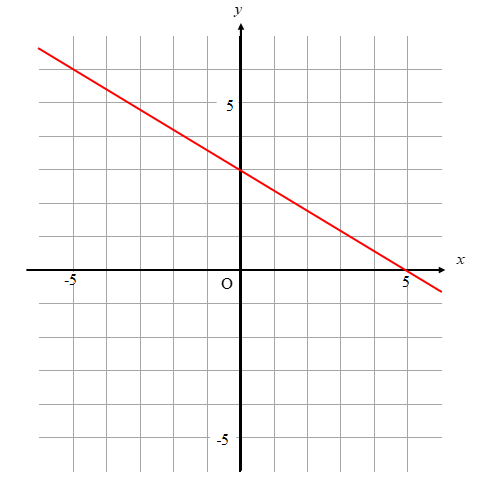
(3)
(4)\(20x+16y\)(点)
(5)\(75cm^3\)
間違っていた部分は解説を見て
理解を深めておこう!
問題の解説
それでは各問題の解説をしていきます。
間違っていたところは念入りに確認しておきましょう!
(1)の解説!
この計算問題は引っかけポイントが2か所あります。
まず1つ目は累乗の計算です。
$$(-2)^3=(-2)\times(-2)\times(-2)=-8$$
$$-3^2=-3\times 3=-9$$
符号に気をつけながら累乗の計算をしてくださいね。
$$(-2)^3-(-3^2)\times (-4)$$
$$=-8-(-9)\times (-4)$$
累乗の計算ができたら、次は計算の順番です。
引き算と掛け算では、掛け算を優先して計算しないといけません。
よって
$$=-8-(-9)\times (-4)$$
$$=-8-(+36)$$
$$=-8-36$$
$$=-44$$
累乗の計算が苦手な人はこちらの記事もご参考ください(^^)
(2)の解説!
因数分解にはいくつかのパターンがありますが
今回は共通因数をくくりだすパターンとなります。
\(x^2\)と\(-6x\)の項に共通している因数は\(x\)です。
よって、\(x\)でくくりだして
$$x^2-6x=x(x-6)$$
となります。
(3)の解説!
(3)一次関数\(\displaystyle y=-\frac{3}{5}x+3\)のグラフをかきなさない。
まずは、傾きと切片をそれぞれ読み取ります。
傾きは\(\displaystyle -\frac{3}{5}\)
切片は\(3\)であることが式から読み取ることができます。
グラフをかくときには、まず切片の点を取って
そこから傾き分だけ点を動かして
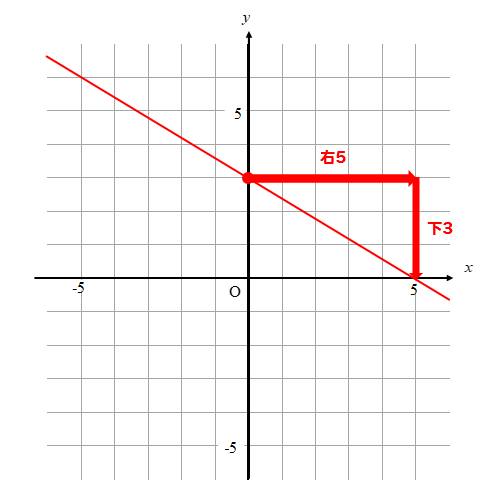
線を引きます。
一次関数のグラフのかき方については
こちらの記事で丁寧に解説しています!
(4)の解説!
で表すことができます。
これを利用して考えていきましょう!
平均を利用する問題では、よく使用する式なので覚えておきましょう。
男子の平均は\(x\)点、人数は20人より
男子の合計点は\(x\times 20=20x\)点となります。
同様に
女子の平均点は\(y\)点、人数は16人より
女子の合計点は\(y\times 16=16y\)点となります。
以上より
クラスのテストの合計点は
男子と女子の合計点を合わせると表すことができるので
\(20x+16y\)点となります。
(5)の解説!
(5)下の図は、三角柱の投影図である。この三角柱の体積を答えなさい。

まず、三角柱の辺がどのようになっているのかを確認しましょう。
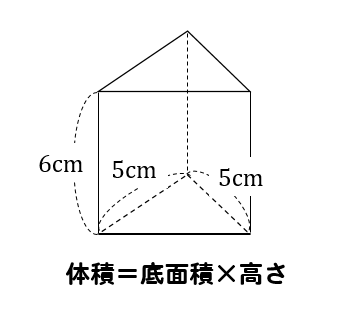
体積は底面積に高さを掛けることで求めることができます。
底面積は三角形なので
$$5\times5\times \frac{1}{2}=\frac{25}{2}$$
よって、体積は
$$\frac{25}{2}\times 6=75$$
となります。
投影図の復習はこちらの記事でどうぞ!
以上
小問演習の第4回でした。
全部解けた人は素晴らしい!
解けなかった人も必ず見直しをして
入試本番では解けるようにがんばっていこう!
ファイトだー(/・ω・)/
小問演習の第5回はこちら!


















コメントを残す