【等式の変形】分数、かっこなど、解き方をパターンごとに問題解説！

今回は中2で学習する

『等式の変形』の問題演習をやっていこう！

 

ここの単元は、説明をうだうだ聞くよりも

実際に手を動かしながら身につけていくことが大切です。

 

この記事ではパターン別に8問用意しました。

これらの問題を解きながら

式変形のポイントなどを学んでいきましょう。

 

分数やかっこがついている等式は苦手な人が多いので

今回の記事を通して、理解を深めれるよう

一緒にがんばっていこう！

 

いくぞーーー！！

 

今回の記事はこちらの動画でも解説しています(/・ω・)/

 

【基本形】問題(1)の解説！

これは等式変形レベル1問題です。

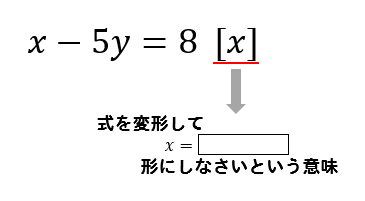
等式の変形というのは

式を変形して、左辺を[   ]内の文字だけにしなさい

という問題です。

 

今回は左辺をxだけにしたいので

ジャマな－5yは移項して右辺に持って行ってやります。

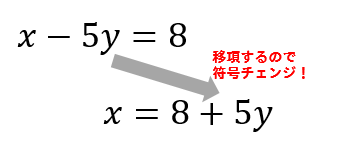
すると左辺がxだけになったので

答えは

$$x=8+5y$$

となりました。

 

移項すると符号チェンジでしたね！

それだけ覚えておけば大丈夫な問題でした。

 

【係数がジャマ】問題(2)の解説！

左辺をxだけにしたいので

まずは、ジャマなyを移項で右辺に持っていきます。

$$3x=6-y$$

すると

あれ？

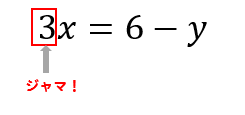
まだジャマなやつがいるぞ…

 

3はxに直接掛けられている係数という数なので

移項することができません。

このジャマな3を右辺に持っていくためには

割り算をしてやります。

(割り算は符号チェンジしないからね！)

$$3x=6-y$$

$$x=(6-y)\div3$$

$$x=\frac{6-y}{3}$$

これで左辺がxだけになりましたね。

あれ、なんで分数になるんだっけ？という方は

こちらで文字式のルールを確認しておいてね！

 

ここで一つ気を付けておいて欲しいのが

こんな感じで約分しちゃダメだからね！

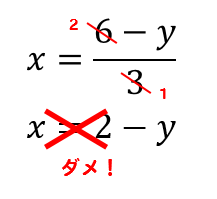
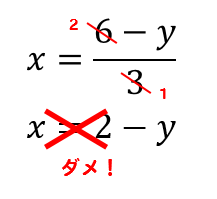
このように、全部が約分できる場合はOKですが

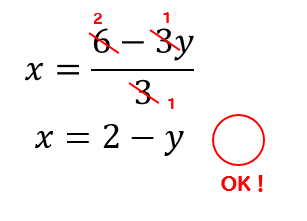
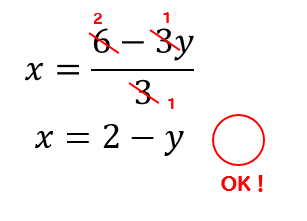
部分的にしか約分できないときは、やっちゃダメ！

どうしても約分したいぜっていう人は

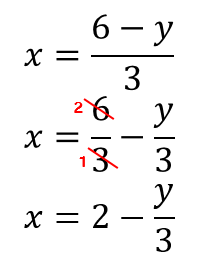
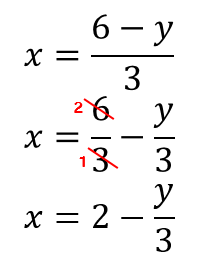
このように分けてやってから約分してください。

 

【マイナスがジャマ】問題(3)の解説！

まずはジャマな－12xを移項で右辺に持っていきます。

$$-12x-3y=-6$$

$$-3y=-6+12x$$

次はyに直接くっついている－3を割って

右辺に持っていきたいところですが

マイナスがついていると計算がややこしくなってしまうので

割り算をする前に、全体にマイナスを掛けて

符号をチェンジしてやります。

$$-3y\times(-1)=(-6+12x)\times(-1)$$

$$3y=6-12x$$

このようにジャマな－3を+3に変えてから割っていきます。

$$y=(6-12x)\div3$$

$$y=\frac{6-12x}{3}$$

今回は、全部が約分できるので

$$y=2-4x$$

としてやります。

 

－3で割ってやってもいいのですが

多くの人が、ここで符号ミスを起こしてしまいます。

そんなミスをしてしまうくらいなら

符号だけを一旦チェンジさせてやっていきましょう。

 

 

【かっこがある】問題(4)の解説！

かっこがついている等式ですね。

分配法則を使って、かっこをはずしたくなっちゃいますが…

分配しません！！

計算をラクにするためには分配法則をしないほうが良いです。

 

まず、目的の文字bが右辺にあるので

左辺と右辺をひっくり返して

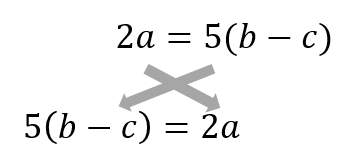
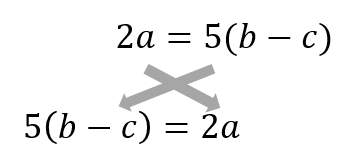
式変形をする準備をします。

 

ここから

かっこの前についている5を

分配法則でかっこをはずすのではなく

右辺に割り算で持って行ってやります。

$$b-c=2a\div5$$

$$b-c=\frac{2}{5}a$$

ここからはジャマな－cを移項で右辺に持っていきます。

$$b=\frac{2}{5}a+c$$

これで左辺はbだけになりました。

 

かっこの前に数や文字がある場合には

分配法則を使わず、先に右辺に持っていくと

計算がラクになります。

 

 

【分数がある】問題(5)の解説！

いよいよ分数の形に挑戦です。

分数は消す！

これがポイントです。

 

まずは、hを左辺に持っていくために

左辺と右辺をひっくり返します。

$$V=\frac{1}{3}\pi r^2h$$

$$\frac{1}{3}\pi r^2h=V$$

ここから分数を消すために

分母にある数3を両辺に掛けます。

$$\frac{1}{3}\pi r^2h\times3=V\times3$$

$$\pi r^2h=3V$$

このように、分数は消してしまいましょう！

 

ここまできたら、hにくっついている

πr²をまとめて、割り算で右辺に持っていきます。

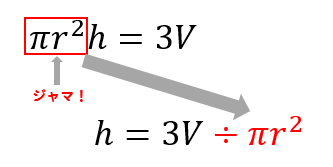
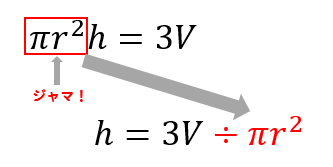
よって

$$h=\frac{3V}{\pi r^2}$$

 

 

分数だし、ジャマなものがたくさんついてるし…

って思っちゃいますが

 

分数は消せばよい！

ジャマなモノは、まとめて割り算できる！

だから、そんなに難しくないですね。

楽勝っす！

 

【分数が2個】問題(6)の解説！

こちらは分数が2個も…！？

 

これもさっきと同じように

まずは、分数を消します。

分母にある数が3と4なので

これらの最小公倍数である12を両辺に掛けます。

$$(\frac{x}{3}+\frac{y}{4})\times12=1\times12$$

$$4x+3y=12$$

ここまで来れば、今までのやり方通り進めていきます。

ジャマな4xを右辺に移項

$$3y=12-4x$$

yにくっついている3を割り算で右辺に持っていく

$$y=(12-4x)\div3$$

$$y=\frac{12-4x}{3}$$

これで完成です！

 

分数が2個ある場合には

分母にある数の最小公倍数を掛けて分数を消してやりましょう。

 

 

【分子にたくさん】問題(7)の解説！

うぉー分数の上にたくさん乗ってる…

 

こんなときでも、基本は一緒

分数よ、消え去れ！！

 

まずは、aを左辺に持ってくるために

左辺と右辺をひっくり返します。

$$m=\frac{3a+2b}{5}$$

$$\frac{3a+2b}{5}=m$$

 

ここから、分母にある5を両辺に掛けて分数を消します。

$$\frac{3a+2b}{5}\times5=m\times5$$

$$3a+2b=5m$$

次は、ジャマな2bを右辺に移項して持っていきます。

$$3a=5m-2b$$

aにくっついている3を割り算で右辺に持っていきます。

$$a=(5m-2b)\div3$$

$$a=\frac{5m-2b}{3}$$

これで完成！

 

やっぱり分数は消す！

これに尽きますね。

 

【分数にかっこも】問題(8)の解説！

分数にかっこがミックス！？

ラスボス感がありますね。笑

 

それでは、倒していきましょう。

まずはaを左辺に持っていくために

左辺と右辺をひっくり返します。

$$S=\frac{(a+b)h}{2}$$

$$\frac{(a+b)h}{2}=S$$

分数を消すために両辺に2を掛けます。

$$\frac{(a+b)h}{2}\times2=S\times2$$

$$(a+b)h=2S$$

さて、かっこについているhは

分配法則ではなく、右辺に持っていく！でしたね。

$$a+b=2S\div h$$

$$a+b=\frac{2S}{h}$$

最後の仕上げにジャマなbを右辺に移項しましょう。

$$a=\frac{2S}{h}-b$$

これで完成！

ラスボス倒しだぞーーー！

 

【特典】保護者さん、学生さん用の追加教材を用意しました！

お疲れ様でした！

ここまでのところで等式の変形の基礎はバッチリ仕上がったと思います！

あとはいろんな問題にチャレンジして理解を定着させていきたいですね(‘ω’)ノ

 

というわけで最後まで取り組んでくれたお礼として、理解を深めるための追加演習をプレゼントします。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます。

この課題をクリアすれば等式変形はあなたの武器になります＾＾

これからのテストで、等式変形はぜーんぶマルにしちゃいましょう(‘ω’)ノ

 

 

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定です。

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

式変形のポイントまとめ

以上、8問お疲れ様でした。

全ての問題において

やっているのは単純なことだし

共通していることばかりでしたね。

 

その中でもいくつかの式変形のポイントをまとめておきます。

• 目的の文字が右辺にあるときは、左辺右辺をひっくり返す

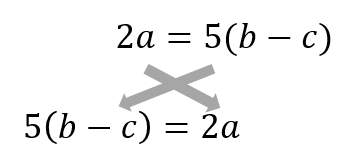
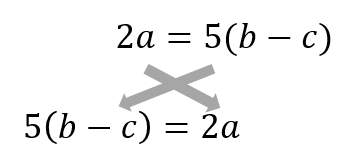
• ジャマものは移項、直接くっついているジャマものは割り算

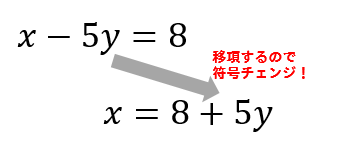
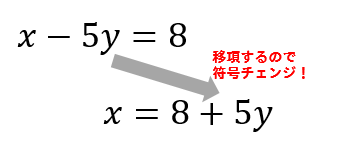
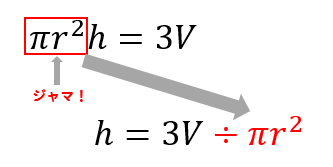
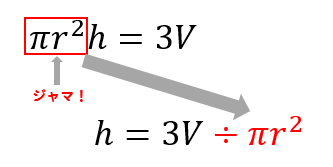
• 分数は消す！

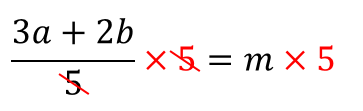
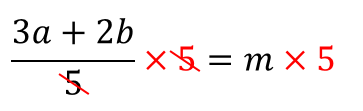
• かっこについている数は、分配ではなく右辺に割り算

 

 

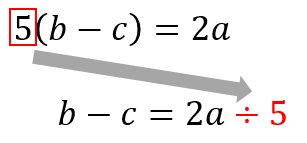
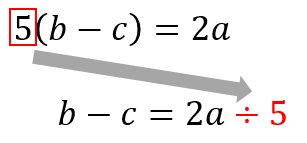
等式の変形ができるようになると

点数アップ間違いなし！

たくさん練習して、しっかりと身につけていきましょう。

ファイトだー！！

 

等式変形の演習問題はこちらからどうぞ＾＾

＞＞＞【高校入試】等式変形の入試問題に挑戦してみよう！