高校入試対策演習
小問集合の第2回目です！
目安時間は5分です。
挑戦してみましょう(^^)
第2回 小問集合
（1） \((-3)^2+(-1)^3\) を計算しなさい。
（2）\(\displaystyle \sqrt{75}-\frac{6}{\sqrt{3}}\)を計算しなさい。
（3）\(x \)kgの\(7\)％は何㎏か、\(x\)を使って表しなさい。
（4）3枚の硬貨を同時に投げるとき、2枚が表で1枚が裏の出る確率を求めなさい。
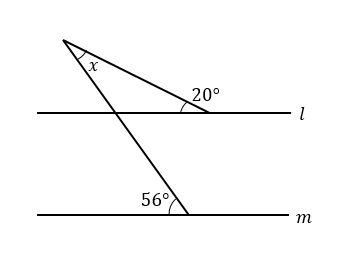
（5）下の図において、2直線\(l, m\)は平行である。このとき、\(∠x\)の大きさを求めなさい。
問題が解けた人は↓で答え合わせをしていきましょう！
YouTube動画でも問題解説しています(^^)
毎週金曜に、小問演習のプリント＆解説動画をお届けしています。
数学の力を伸ばすためには問題演習が欠かせません。
登録は無料ですので、ぜひご活用ください＾＾
登録直後にこれまでに配信してきた小問課題をまとめてプレゼント。
今すぐ演習にとりかかれますよ！
問題の解答
解答はこちらです。
答え合わせしてみましょう(^^)
答え
（1）\(8\)
（2）\(3\sqrt{3}\)
（3）\(\displaystyle \frac{7}{100}x{または}0.07x\)
（4）\(\displaystyle \frac{3}{8}\)
（5）\(36° \)
間違っていた部分は解説を見て
理解を深めておこう！
問題の解説
それでは各問題の解説をしていきます。
間違っていたところは念入りに確認しておきましょう！
（1）の解説！
この問題で気をつけないといけないのは
累乗の計算！
累乗の計算がバッチリな人には楽勝な問題だったかと思いますが
簡単に確認しておきましょう。
$$\LARGE{(-3)^2=(-3)\times (-3)=9}$$
$$\LARGE{(-1)^3=(-1)\times (-1)\times (-1)=-1}$$
累乗の計算とは
右上にある小さな数(指数)だけ繰り返し掛けなさい。
という計算でしたね。
これを利用していくと
$$\LARGE{(-3)^2+(-1)^3}$$
$$\LARGE{=9-1}$$
$$\LARGE{=8}$$
他にも累乗の計算は複雑なモノが多いから
不安な人はこちらの記事で確認しておいてね！
（2）の解説！
分母にルートが出てきたら、まずは…
有理化をしましょう！
有理化というのは
分母にあるルートを、分母・分子ともにかけて
分母のルートを消してやる作業のことでしたね。
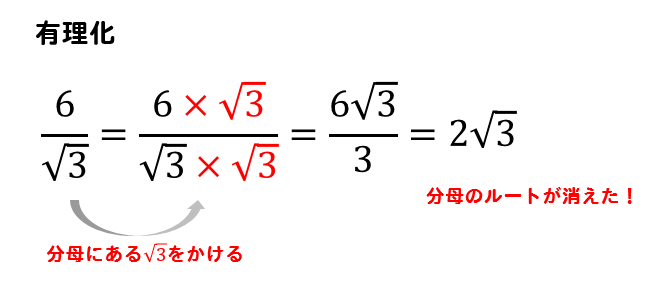
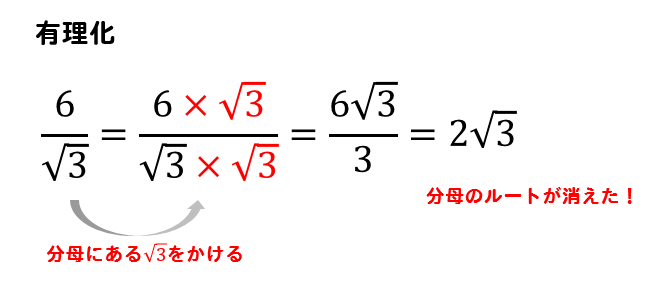
あとは\(\sqrt{75}=\sqrt{5^2\times 3}=5\sqrt{3}\)としてやって
計算を進めていきます。
$$\LARGE{\displaystyle \sqrt{75}-\frac{6}{\sqrt{3}}}$$
$$\LARGE{=5\sqrt{3}-2\sqrt{3}}$$
$$\LARGE{=3\sqrt{3}}$$
（3）の解説！
7％を分数、または小数で表すことができれば楽勝な問題です。
7％というのは
全体を100と考えたときの7個分ということを表しているので
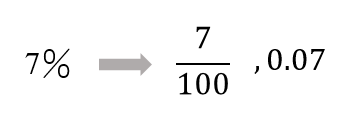
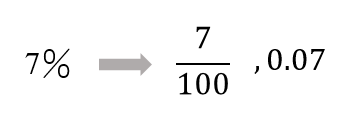
よって、\(x\)の7%というのは
\(x\)を100個に分けた7個分だから
$$\LARGE{\displaystyle \frac{7}{100}x{または}0.07x}$$
となります。
割合の問題では他にも
7％増加、7％減少は？
1割は？
など、様々なパターンの問題があります。
これらの問題を
こちらの記事でまとめているので確認しておいてくださいね。
（4）の解説！
硬貨を投げるときの確率問題は
樹形図を書いて考えましょう！
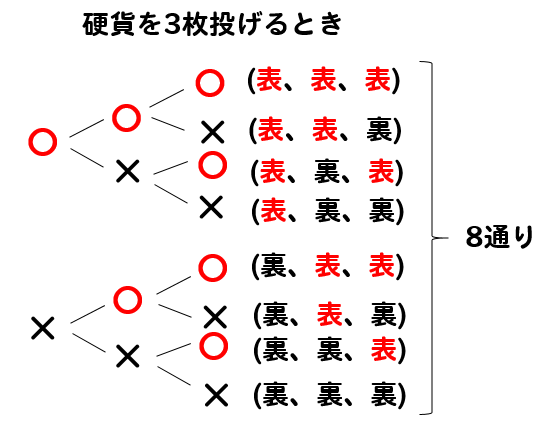
この樹形図の中から
2枚が表、1枚が裏になっているものは
3つあることがわかります。
よって、全部で8個ある中で該当するものは3個なので
確率は\(\displaystyle \frac{3}{8}\)となります。
硬貨の確率は樹形図を練習しておけばバッチリ！
（5）の解説！
（5）下の図において、2直線\(l, m\)は平行である。このとき、\(∠x\)の大きさを求めなさい。
平行な線が出てくると考えなくてはいけないのが
同位角、錯角ですね。
この問題では、56°の同位角を考えて
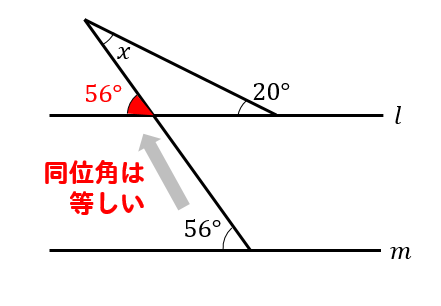
三角形の外角の性質を利用すると
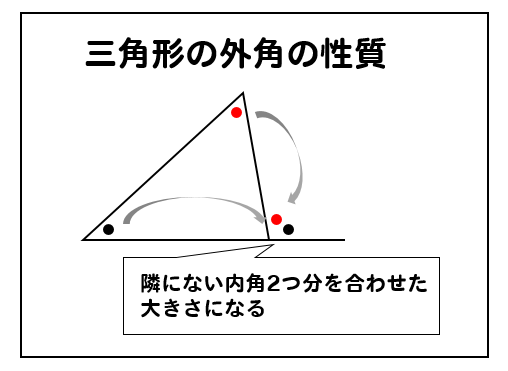
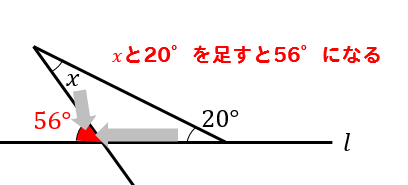
$$\LARGE{x+20=56}$$
$$\LARGE{x=36}$$
このように求めてやることができます。
平行な線と角度の問題であれば
同位角、錯角を使って
角が等しくなるところを見つけていくようにしましょう。
以上
小問演習の第2回でした。
全部解けた人は素晴らしい！
解けなかった人も必ず見直しをして
入試本番では解けるようにがんばっていこう！
ファイトだー(/・ω・)/
小問演習～第3回～はこちら
コメントを残す