【円周角の定理】円の中にブーメラン型があるときの角度の求め方！

今回は円周角の定理とブーメラン型の角度を混ぜ合わせたような

 

こーんな形の図形の問題を解説していきます。

 

 

一見、普通の円周角の問題じゃない？？

と思ってしまうのですが

円周角の定理だけではちょっとつまづいてしまう問題です。

 

 

というわけで

この問題を解くために必要な知識と

解き方を解説していきます。

問題を解くために知っておきたいこと

まずは、円周角の定理をおさらいしておきましょう！

 

• 同じ弧に対する中心角の大きさは円周角の大きさの2倍になる。

 

• 同じ弧に対する円周角の大きさは等しい

 

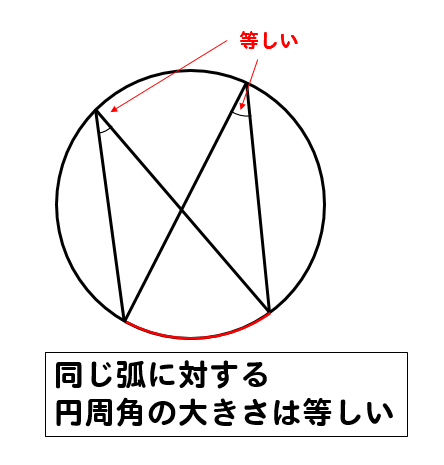
この2つは円周角の定理の基本です。

必ず覚えておきましょうね！

 

 

そして、次はブーメラン型の図形の特徴。

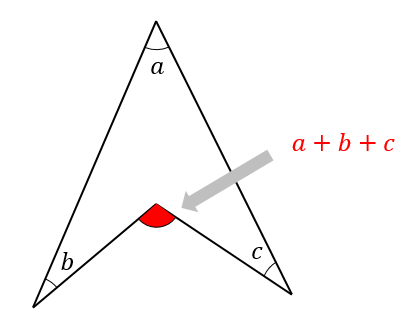
このようなブーメラン型の図形は

とがっている角を全部合わせると凹み部分の角と同じ大きさになります。

 

 

今回の問題では

これら2つのことを利用しながら解いていきます。

それでは、問題を１つずつ解説していきます。

 

問題の解説

それではそれぞれの問題を解説していきます。

（1）の解説！

 

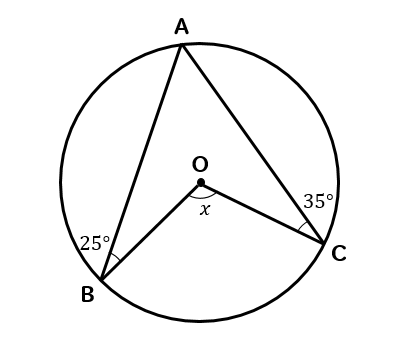
この図形では

ブーメラン型があるなーってことに気が付きますよね！

 

 

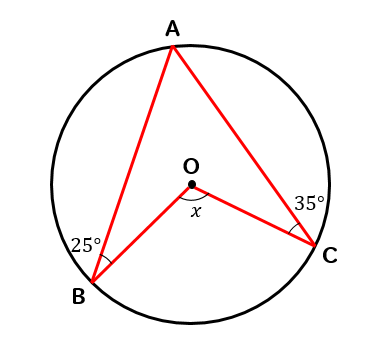
ということは

\(∠A+∠B+∠C\)を計算すれば

凹み部分の\(x\)の大きさを求めることができると考えることができます。

 

円周角の定理を使って考えると

\(\displaystyle ∠A=\frac{1}{2}x\)となるので

 

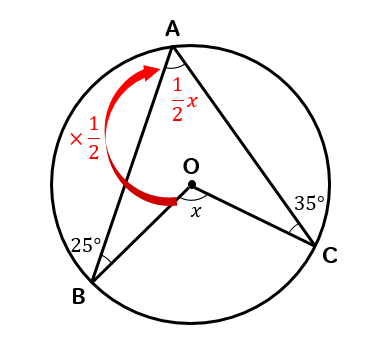
ブーメラン型の特徴より

$$\LARGE{\frac{1}{2}x+25+35=x}$$

$$\LARGE{\frac{1}{2}x-x=-60}$$

$$\LARGE{-\frac{1}{2}x=-60}$$

$$\LARGE{x=120}$$

と求めてやることができます。

 

 

また、ブーメラン型の特徴は使わずに

補助線を引きながら求める方法もあります。

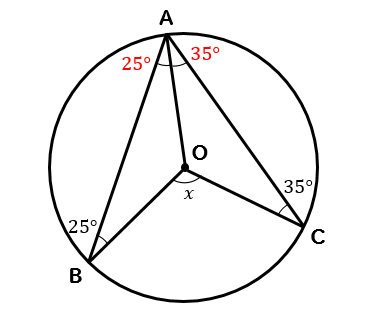
\(OA\)に補助線を引いてやると

\(OA,OB,OC\)は全て円の半径だから、同じ長さになるね。

だから、\(△OAB,△OAC\)は二等辺三角形になります。

 

すると

二等辺三角形の底角は等しくなるから

\(∠A\)の部分が25°と35°を合わせた60°になるということがわかります。

 

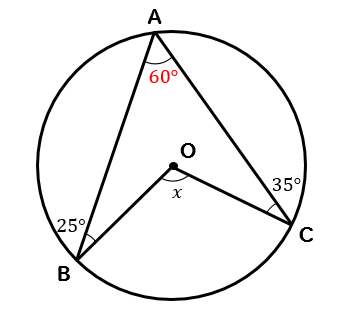
そうすれば、あとは円周角の定理を使って

中心角である\(x\)の大きさを求めれば完了です。

$$\LARGE{x=60 \times 2=120}$$

 

 

ブーメラン型、補助線

自分に合った解き方でやってみてくださいね(^^)

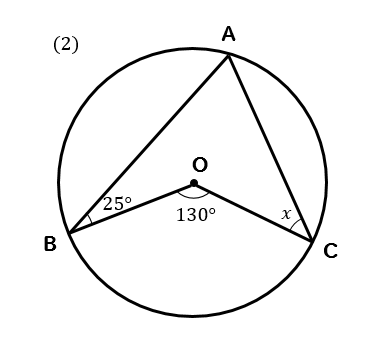
（2）の解説！

 

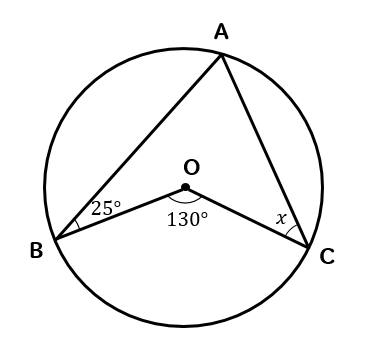
これも円の中にブーメラン型がある図形ですね。

（1）と同様に

\(∠A,∠B,∠C\)を合わせると、凹み部分の130°になることがわかります。

 

\(∠A\)は円周角の定理より

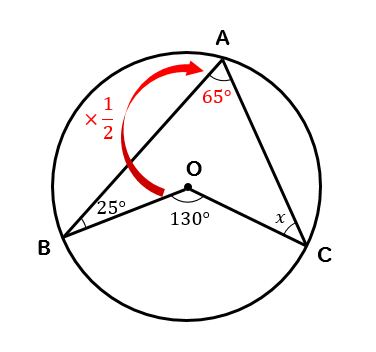
65°になることがわかるので

 

 

ブーメラン型の特徴より

$$\LARGE{x+25+65=130}$$

$$\LARGE{x=130-90}$$

$$\LARGE{x=40}$$

となりました。

 

この問題では

（1）のように補助線を使って考えようとすると

少し複雑な計算になってしまうので

ブーメラン型の特徴を使っていけば良いでしょう！

 

凹みの部分が\(x\)であれば

ブーメラン、補助線どちらでも！

 

ブーメランの中に\(x\)があるときは

ブーメラン一択で！

 

と思っておけば大丈夫です(^^)

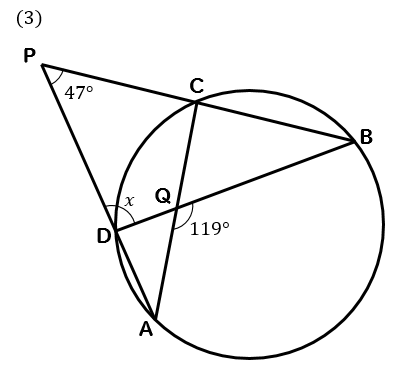
（3）の解説！

 

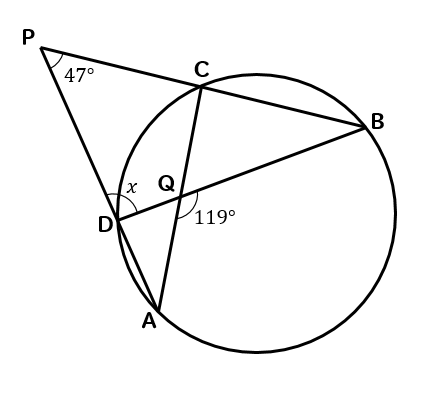
ブーメランが円から飛び出しちゃってます(^^;

だけど、これも同じように考えればOKです。

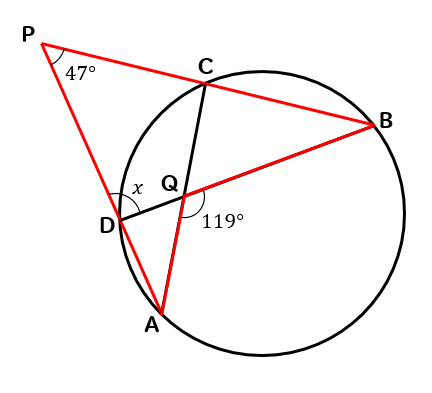
このようにブーメランの形を見つけることができるので

\(∠A,∠B,∠P\)を合わせれば、凹み部分の119°になることがわかります。

 

 

\(A\)も\(B\)も角がわからない状況なので困ってしまいますよね。

でも、それぞれの角は円周角の定理から

同じ大きさになることがわかります。

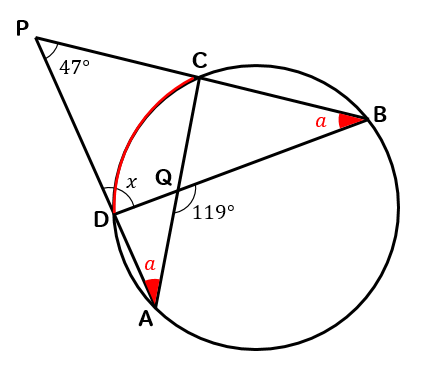
それぞれの角を\(a\)としてやって

ブーメラン型の特徴を使っていくと

 

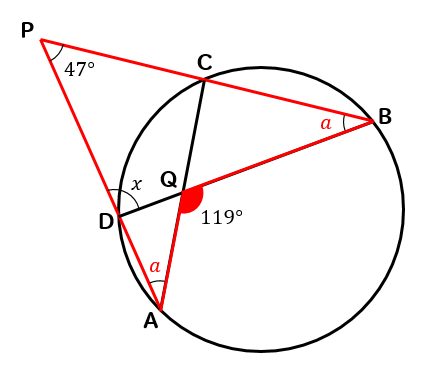
$$\LARGE{a+a+47=119}$$

$$\LARGE{2a=119-47}$$

$$\LARGE{2a=72}$$

$$\LARGE{a=36}$$

となります。

 

 

\(a\)の大きさが分かったところで

\(△PDB\)に注目すると、内角の和が180°になるので

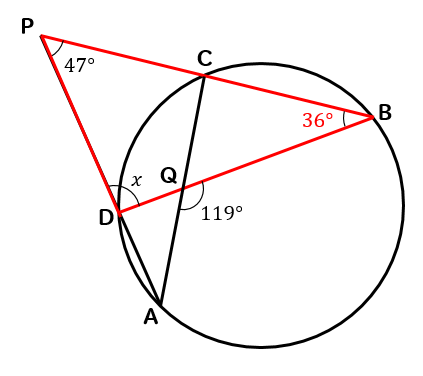
$$\LARGE{47+36+x=180}$$

$$\LARGE{x=180-83}$$

$$\LARGE{x=97}$$

 

となりました。

ちょっと計算が長かったですが

これもブーメラン型の特徴を覚えておけば

大丈夫そうですね(^^)

 

 

ブーメラン型の円周角問題　まとめ

お疲れ様でした！

円の中にブーメラン型を見つけたときには

今回のような解き方を思い出してみてください！

 

とがっている角を全部合わせると

凹み部分になる！

 

これがブーメラン型の特徴でしたね。

しっかりと覚えておきましょう。

 

 

でも、なんでこんな特徴になるんだっけ？

という方はこちらの記事も参考にしてみてくださいね。

 

 

まだまだ円周角の定理が不安だな…という方は

こちらにも円周角の定理に関する問題を用意しているので

ぜひ挑戦してみてください。

ファイトだー(/・ω・)/

 

高校入試で使える公式集をプレゼント！

 
高校入試で使える公式をまとめた教材を作成しました！
 
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/

これは知らないと損をするかも…！？
 
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
 
こちらから公式集を無料で手に入れちゃってください！

ご登録いただいたメールアドレスに教材を送らせていただきます。
 
 
中学生メルマガ講座では、今回のプレゼントのほか


などのプレゼント企画をやっております。
 
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)