今回の記事では「還元算」の解き方について解説していきます。
還元算とは
上の式の☐に当てはまる数を求めるような問題のことですね。
☐の数字を求めるために、逆算をすることによって計算をしていきます。
還元算を解くための基礎!
還元算を解くためには逆算をマスターしておく必要があります。
覚えておきたいのが次の計算だ!
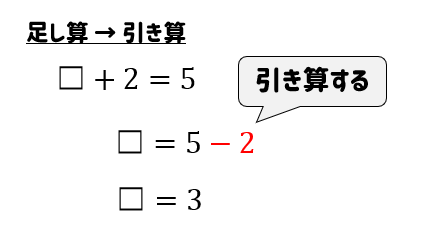

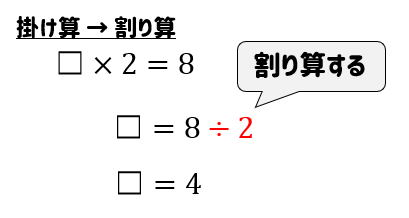

このように、計算することで☐にあてはまる数を求めることができます。
足し算 ⇔ 引き算
掛け算 ⇔ 割り算
というように逆の計算をすることになります。
これくらい暗算で計算できるよー
って声が聞こえてきそうですが、応用問題になると暗算では太刀打ちできないくらいの計算がでてきます。
そのときには、逆算のルールをしっかりと覚えておかないと戦えなくなっちゃうからね。
しっかりと頭に入れておいてください。
更に、気を付けておきたい計算が2つほどあります。

これは計算がひっくり返ってないよね。
☐が計算の右側にある場合の引き算と割り算は注意が必要だね!
では、逆算のコツをつかむために練習問題に挑戦してみましょう!
還元算の基礎問題の練習!
次の☐に入る数を求めましょう。
$$☐+10=18$$
次の☐に入る数を求めましょう。
$$☐-25=9$$
次の☐に入る数を求めましょう。
$$☐\times 7=56$$
次の☐に入る数を求めましょう。
$$☐\div 12=3$$
次の☐に入る数を求めましょう。
$$15-☐=3$$
次の☐に入る数を求めましょう。
$$48\div ☐=12$$
還元算、複雑な逆算をマスターしよう!
では、還元算の基礎編はクリアだね!
次はちょっと複雑な逆算についてやっていこう。
例えば、次のような問題。
次の☐に入る数を求めましょう。
$$☐\times 2 -3=5$$
いろんな計算が混じっていて、どこから逆算していくのか分かりにくいね…
この場合には、通常であればどの順で計算をするのかを考えます。
計算順番は次のようにやってきますよね。
- かっこの中
- 掛け算、割り算
- 足し算、引き算
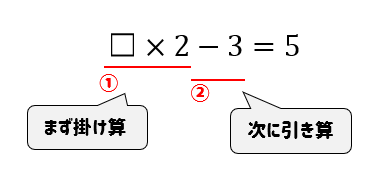
なので、今回の計算ではこのような計算順番になります。
逆算とは、これを逆にたどって計算をしていきます。
つまり、最初に②である引き算の部分を逆算します。
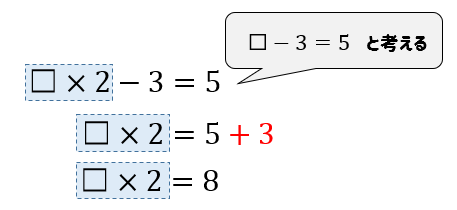
すると、このようになりますね。
ここまでくれば、\(☐\times 2=8\) となるので基礎編でやった逆算で☐が求めれますね!
最後に①の掛け算を逆算すれば完成です。
$$\begin{eqnarray}☐\times 2&=&8\\[5pt]☐&=&8\div 2\\[5pt]☐&=&4 \end{eqnarray}$$
このように、複雑な計算が出てきても計算順序を考えて、しっかりと逆算していけば大丈夫だね!
答えが不安であれば、☐に数をあてはめて確かめをしてみてください(^^)
ってことで、練習問題に挑戦してみましょう。
還元算の応用問題の練習!
次の☐に入る数を求めましょう。
$$8+☐\times 5=28$$
次の☐に入る数を求めましょう。
$$(☐+2)\times 5-3=27$$
次の☐に入る数を求めましょう。
$$15-\{(☐+2)\times 3-8\}=8$$
還元算の文章問題
還元算の逆算について理解が深まってきたところで、最後に文章問題に挑戦していきましょう!
☐にあてはまる数を求めましょう。
☐から5を引いてから4倍し、その積から10を引くと18になる。
まずは、文章を式にしていきましょう。
すると、次のような式ができあがります。
$$(☐-5)\times 4-10=18$$
引き算を最初に計算するので、かっこをつけ忘れないように気を付けてね!
式ができれば逆算で☐に当てはまる数を求めましょう。
$$\begin{eqnarray} (☐-5)\times 4-10&=&18\\[5pt] (☐-5)\times 4&=&18+10\\[5pt] (☐-5)\times 4&=&28\\[5pt] ☐-5&=&28\div 4\\[5pt]☐-5&=&7\\[5pt]☐&=&7+5\\[5pt]☐&=&12\end{eqnarray}$$
答え
$$12$$
線分図を使って考えると次のような図になります。
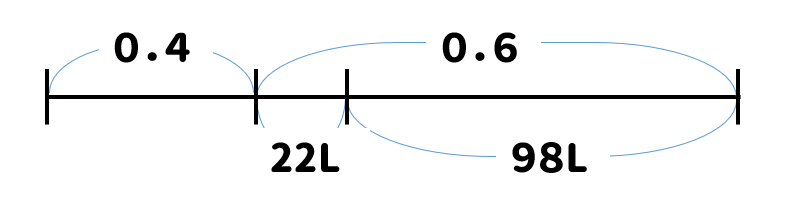
つまり、全体の60%が\(22+98=120L\) ということがわかります。
水そうに入っていた水の量を☐とすると
$$☐\times 0.6=120$$
という式を作ることができます。
$$\begin{eqnarray} ☐\times 0.6&=&120\\[5pt]☐&=&120\div 0.6\\[5pt]☐&=&200\end{eqnarray}$$
答え
$$200L$$
還元算まとめ!
お疲れさまでした!
複雑な計算であっても、しっかりと手順通りに逆算することができれば大丈夫ですね(^^)
ただ、慣れるまでは苦労すると思います。
まずは練習あるのみだ!
ファイト(/・ω・)/

















コメントを残す