今回は中3で学習する平方根の単元から
「ルートを含む式の展開」について取り上げていきます。
挑戦するのはこちらの7題！
それぞれ乗法公式と組み合わさった計算になっています。
ちょっとややこしくてミスが起こりやすいものなので、途中式をていねいに解説していきますね！
動画でサクッと理解したい方はこちらをどうぞ！
（1）の解説
これは一番基本的な計算ですね。
分配法則を使ってカッコ内にかけていきましょう！
\(\color{red}{(\sqrt{3})^2=3}\) のようにルートが2乗になると中身の数になるというところもポイントです。
\((\sqrt{3})^2=\sqrt{9}=3\)
このように計算していると時間がかかってしまうので、サクッと求めれるようにしておきましょう。
（2）の解説
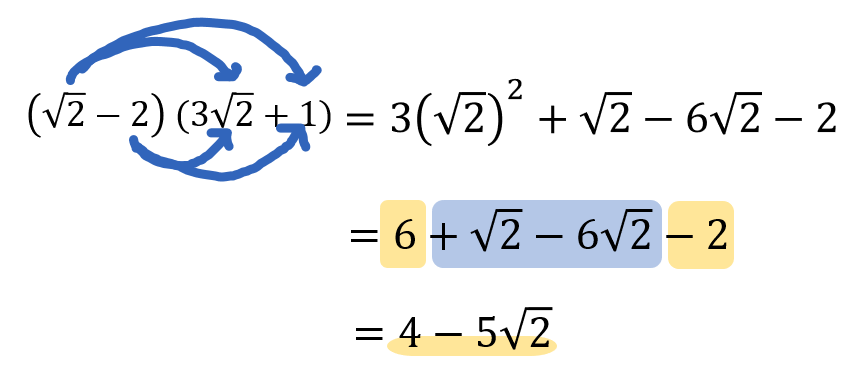
こちらの計算も分配法則を使って、それぞれにかけ算をして解いていきましょう。
ミスが起こりやすいのでしっかりと途中式をかきながら進めていってくださいね！
この部分の計算でミスが起こりやすいので注意です(‘◇’)ゞ
（3）の解説
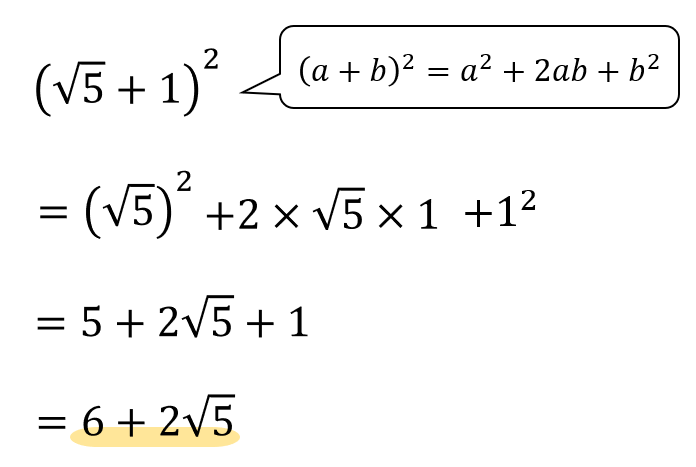
ここでは2乗の乗法公式に当てはめながら計算を進めていきましょう。
2乗の乗法公式では
「2乗、かけて2倍、2乗」
このリズムで計算していけばよかったですね＾＾
公式の使い方はこちらでも解説しているので参考にしてください！
（4）の解説
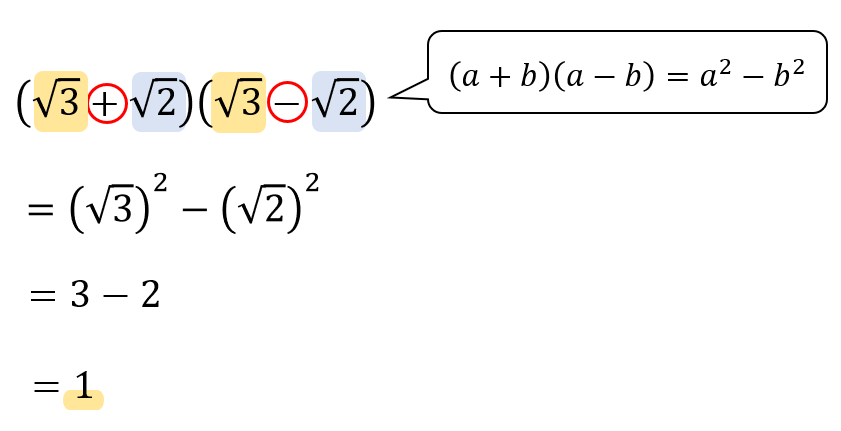
「足してと引いて」になっている展開は「2乗ひく2乗」で計算していけばよかったですね！
ルートは2乗されるとシンプルな値になるので、暗算でサクッと計算できるようにしておきたいです( ｀ー´)ノ
（5）の解説
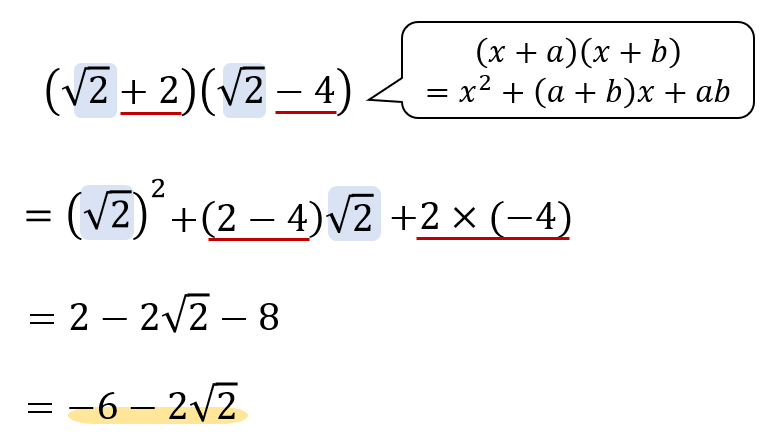
これは見た目がちょっとややこしいですね。汗
\(\sqrt{2}\)のところが共通部分になっているので、乗法公式の\(x\)のところを\(\sqrt{2}\)だとして公式に当てはめていってください。
これに関しても途中式をていねいにかいて、計算ミスが起こらないように注意です！
（6）の解説
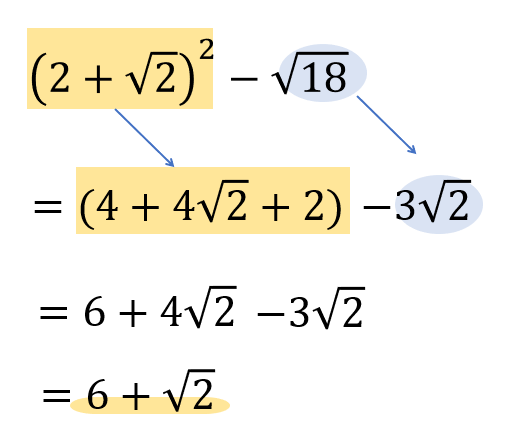
まずは2乗の展開、\(\sqrt{18}\)を簡単にしましょう。
頭の中で計算を進めていくとミスにつながります。
必ず途中式をかいて、段階的に計算していってくださいね。
（7）の解説
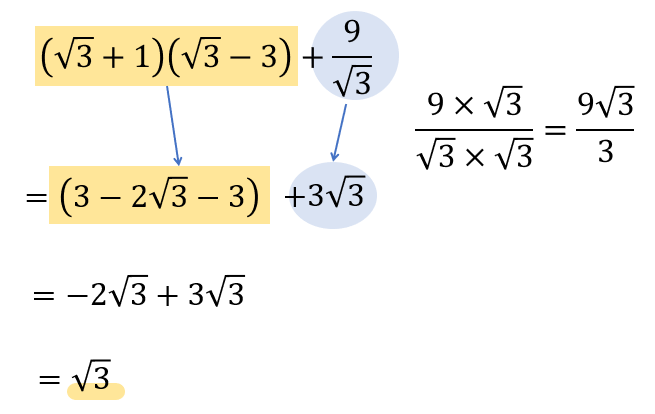
分母にルートがあれば有理化！
これはルート計算の鉄則ですね＾＾
有理化の計算はごちゃっとして計算式が汚くなりがちなので、上の解答のように右端に有理化の過程をメモしながら進めていくといいですよ！
[スタセミ中3バナー]
まとめ！
お疲れさまでした！
今回は演習をしながら理解を深めてもらいましたが、いかがだったでしょうか？
途中式の変形がよくわからん…という方は、動画講義の方をチェックしてみてください。
動画の中では「変形のなぜ」についても詳しくお伝えしていますよ＾＾
ここの計算がクリアできれば、ルートはバッチリかな( ｀ー´)ノ
完璧にこなすためには、かなりの練習量が必要になりますが粘り強く取り組んでいきましょう！
ファイトだ(/・ω・)/
コメントを残す