【平方根】ルートの計算方法まとめ！問題を使って徹底解説！

今回は中3で学習する平方根の単元から

ルートの計算方法についてまとめていくよ！

ルートの計算とは、以下の4つに大きく分けられます。

それでは、それぞれの計算について

問題を使いながら解説していくよー！

【ルートの変形についての解説動画】

【ルートの乗除についての解説動画】

【分母の有理化についての動画】

【ルートの加減についての解説動画】

ルートの中を簡単にする計算

ルートは中に2乗となる数があれば、外に出してやることができます。

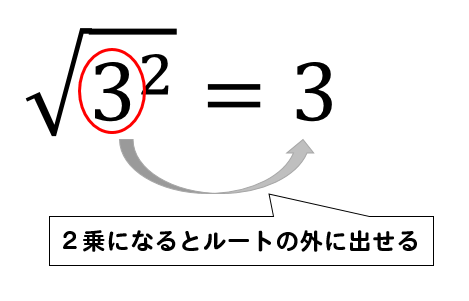
このことを利用して、ルートの中に2乗となる数を見つけて外に出していきましょう。

（1）の問題解説

ルートの中身である24を素因数分解すると

$$\sqrt{24}=\sqrt{2^2\times 2\times 3}$$

$$=2\sqrt{2\times 3}$$

$$=2\sqrt{6}$$

このように、2乗になる数を見つけて外に出してやれば

ルートの変形は完成です！

（2）の問題解説！

336は大きな数なので分かりにくいですが

丁寧に素因数分解していきましょう。

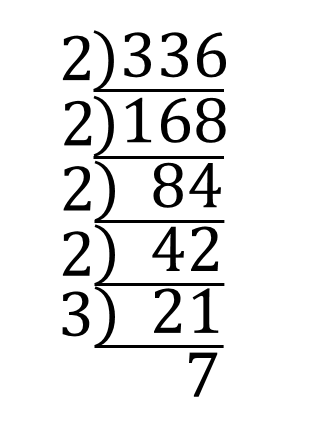
$$\sqrt{336}=\sqrt{2^2\times 2^2\times 3\times 7}$$

$$=2\times 2\sqrt{3\times 7}$$

$$=4\sqrt{21}$$

（3）の問題解説！

分数の形になってはいますが、特別な考え方はありません。

まずは、分子の\(\sqrt{12}\)を変形しましょう。

$$\sqrt{12}=\sqrt{2^2\times 3}=2\sqrt{3}$$

よって

$$\frac{\sqrt{12}}{4}=\frac{2\sqrt{3}}{4}$$

$$=\frac{\sqrt{3}}{2}$$

ルートの中身を簡単にする問題については、こちらの記事でも詳しく解説しています。

＞＞＞【平方根】a√bの形に変形するやり方とは？

もっと問題演習したい方は、参考にしてみてください！

ルートの掛け算・割り算

ルートの掛け算・割り算はとてもシンプルです。

$$\Large{\sqrt{2}\times \sqrt{3}=\sqrt{2\times 3}}$$

$$\Large{\sqrt{6}\div \sqrt{3}=\sqrt{6\div 3}}$$

というように、ルートの中身をそのまま掛けたり割ったりすれば良いだけです。

それでは、それぞれの問題の解き方を見ていきましょう。

（1）の問題解説！

ルートの中身をそのまま掛け合わせればOKです。

$$\sqrt{3}\times \sqrt{5}=\sqrt{3\times 5}$$

$$=\sqrt{15}$$

（2）の問題解説！

ルートの中身をそのまま掛けていけば良いのですが

32と8の掛け算は、ちょっとめんどうですよね(^^;

\(\sqrt{32}\)と\(\sqrt{8}\)はそれぞれ中身を簡単にできるので

$$\sqrt{32}\times (-\sqrt{8})=4\sqrt{2}\times (-2\sqrt{2})$$

$$=-8\sqrt{2\times 2}$$

$$=-8\times 2$$

$$=-16$$

となります。

このように、ルートの掛け算では

ルートの中身を簡単にしてから計算をスタートすると

ちょっとだけ計算がラクになりますね(^^)

（3）の問題解説！

ルートの中身を簡単にしてから計算をスタートしていきましょう。

$$4\sqrt{2}\times \sqrt{12}\times 2\sqrt{3}$$

$$=4\sqrt{2}\times 2\sqrt{3}\times 2\sqrt{3}$$

$$=4\times 2\times 2\sqrt{2\times 3\times 3}$$

$$=16\times 3\sqrt{2}$$

$$=48\sqrt{2}$$

（4）の問題解説！

割り算も中身をそのまま計算していけばOKです。

$$\sqrt{60}\div \sqrt{3}=\sqrt{60\div 3}$$

$$=\sqrt{20}$$

$$=2\sqrt{5}$$

\(\sqrt{60}=2\sqrt{15}\)と変形してから計算しても良いのですが

割り算の場合には、そのまま計算しても約分などによって簡単に計算できることが多いです。

（5）の問題解説！

これもそのまま計算していきましょう！

$$(-\sqrt{12})\div \sqrt{3}=-\sqrt{12\div 3}$$

$$=-\sqrt{4}$$

$$=-2$$

ルートの有理化

分母にルートを含まない形に変形することを分母の有理化といいます。

分母にあるルートを分母・分子の両方に掛けて計算していくと

$$\Large{\frac{3}{\sqrt{2}}}$$

$$\Large{=\frac{3\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}}$$

$$\Large{=\frac{3\sqrt{2}}{2}}$$

このように分母にルートがない形に変形することができます。

（1）の問題解説！

分母にある\(\sqrt{3}\)を分母・分子に掛けて有理化をしていきます。

$$\frac{2}{\sqrt{3}}=\frac{2\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}$$

$$=\frac{2\sqrt{3}}{3}$$

（2）の問題解説！

分母にある\(\sqrt{2}\)を分母・分子に掛けて有理化していきましょう。

$$\frac{8}{3\sqrt{2}}=\frac{8\times \sqrt{2}}{3\sqrt{2}\times \sqrt{2}}$$

$$=\frac{8\sqrt{2}}{3\times 2}$$

$$=\frac{4\sqrt{2}}{3}$$

（3）の問題解説！

今回の場合、分母にある\(\sqrt{63}\)を有理化に使うと

計算が複雑になってしまいます…

なので、まずは\(\sqrt{63}\)を簡単にしてから

有理化をスタートしていきましょう！

$$\frac{\sqrt{2}}{\sqrt{63}}=\frac{\sqrt{2}}{3\sqrt{7}}$$

$$=\frac{\sqrt{2}\times \sqrt{7}}{3\sqrt{7}\times \sqrt{7}}$$

$$=\frac{\sqrt{2\times 7}}{3\times 7}$$

$$=\frac{\sqrt{14}}{21}$$

ルートの足し算・引き算

ルートの足し算・引き算は文字式と同じように考えて計算します。

$$2a+3a=5a$$

$$2a+5b-4a+3b=-2a+8b$$

文字式では、同じ文字どうしを計算するように

ルートでも同様に

$$2\sqrt{3}+3\sqrt{3}=5\sqrt{3}$$

$$2\sqrt{2}+5\sqrt{3}-4\sqrt{2}+3\sqrt{3}=-2\sqrt{2}+8\sqrt{3}$$

ルートの中身が同じものどうしを計算して

ルートの外の数だけを足したり、引いたりして計算します。

（1）の問題解説！

ルートの外にある数どうしを計算していきます。

$$4\sqrt{3}-\sqrt{3}=3\sqrt{3}$$

（2）の問題解説！

\(\sqrt{7}\)と\(\sqrt{2}\)どうしをそれぞれ計算していきましょう。

$$4\sqrt{7}-\sqrt{2}+3\sqrt{7}-3\sqrt{2}$$

$$=7\sqrt{7}-4\sqrt{2}$$

（3）の問題解説！

√の中身が同じではないので、このままだと計算ができません。

だけど、ルートの中身を簡単にしてやると

$$\sqrt{12}+\sqrt{75}=2\sqrt{3}+5\sqrt{3}$$

となり、ルートの中身が同じになるので計算ができるようになります。

よって

$$\sqrt{12}+\sqrt{75}=2\sqrt{3}+5\sqrt{3}$$

$$=7\sqrt{3}$$

（4）の問題解説！

（3）と同様に、ルートの中身を簡単にしてから計算を進めていきましょう。

$$\sqrt{45}-4\sqrt{3}-\sqrt{20}+\sqrt{12}$$

$$=3\sqrt{5}-4\sqrt{3}-2\sqrt{5}+2\sqrt{3}$$

$$=\sqrt{5}-2\sqrt{3}$$

四則の混じった複雑な計算

ここまで、ルートの四則演算について学んできましたが

最後はいろんな演算が混じった、複雑な計算を練習していきましょう。

（1）の問題解説！

割り算は、ひっくり返して掛け算にして考えていきましょう！

$$\sqrt{21}\div \sqrt{6}\times \sqrt{2}$$

$$=\sqrt{21}\times \frac{1}{\sqrt{6}}\times \sqrt{2}$$

$$=\frac{\sqrt{21}\times \sqrt{2}}{\sqrt{6}}$$

ここで√の中身を約分すると

$$=\sqrt{7}$$

となります。

（2）の問題解説！

まずは掛け算から！

$$\sqrt{10}\times \sqrt{5} -\sqrt{32}$$

$$=\sqrt{50}-\sqrt{32}$$

ここからルートの中身を簡単にして、引き算していきましょう。

$$=5\sqrt{2}-4\sqrt{2}$$

$$=\sqrt{2}$$

（3）の問題解説！

割り算を掛け算に、分母のルートは有理化を！

$$2\sqrt{15}\div \sqrt{3}-\frac{20}{\sqrt{5}}$$

$$=2\sqrt{15}\times \frac{1}{\sqrt{3}}-\frac{20\times \sqrt{5}}{\sqrt{5}\times \sqrt{5}}$$

$$=2\sqrt{5}-\frac{20\sqrt{5}}{5}$$

$$=2\sqrt{5}-4\sqrt{5}$$

$$=-2\sqrt{5}$$

（4）の問題解説！

分配法則を使って計算していきましょう！

$$\sqrt{6}(\sqrt{3}-\sqrt{2})$$

$$=\sqrt{6}\times \sqrt{3}-\sqrt{6}\times \sqrt{2}$$

$$=\sqrt{18}-\sqrt{12}$$

$$=3\sqrt{2}-2\sqrt{3}$$

（5）の問題解説！

乗法公式

$$(x+a)(x+b)=x^2+(a+b)x+ab$$

を使って、計算を進めていきます。

$$(\sqrt{3}+1)(\sqrt{3}+2)$$

$$=(\sqrt{3})^2+(1+2)\sqrt{3}+1\times 2$$

$$=3+3\sqrt{3}+2$$

$$=5+3\sqrt{3}$$

（6）の問題解説！

乗法公式

$$(a+b)^2=a^2+2ab+b^2$$

を使って計算を進めていきましょう。

$$(\sqrt{3}+2)^2=(\sqrt{3})^2+2\times 2\times \sqrt{3}+2^2$$

$$=3+4\sqrt{3}+4$$

$$=7+4\sqrt{3}$$

まとめ

お疲れ様でした！

これでルートの計算はバッチリです(^^)

あとは、学校のワークなどを使って

たくさん練習して、ルートの計算を得意にしていきましょう！

ファイトだー(/・ω・)/