今回は中３で学習する平方根の単元を扱っていきます。
ひとよひとよにひとみごろ～
なんか百人一首にでも出てきそうな一文だけど
数学をやっていると必ず1度は耳にする言葉だよね。
この言葉は何を表しているのかというと
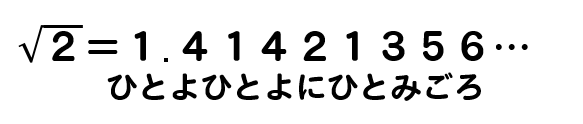
このように\(\sqrt{2}\)の近似値を表しているんですね。
え、そもそも平方根の近似値なんて覚えなきゃいけないの！？
絶対に覚えなきゃいけないということはありません。
おそらく近似値を問うような問題は出ないでしょう。
だけどね
やっぱり覚えておくと便利なこともあるんだよ！
だから、覚えやすいように語呂合わせまで作られてる訳だからね。
ということで
平方根の値を語呂合わせで覚えちゃおう！
Contents
平方根ルートの語呂合わせ
\(\sqrt{2}\)の語呂合わせ
$$\Large{\sqrt{2}=1.41421356\cdots}$$
一夜一夜に人見頃（ひとよひとよにひとみごろ）
一番有名な語呂合わせですね
なんとなーくお月見を連想しちゃうのは私だけ？(^^;
語呂合わせは長いですが、1.41まで覚えておければ十分です。
\(\sqrt{3}\)の語呂合わせ
$$\Large{\sqrt{3}=1.7320508\cdots}$$
人並みに奢れや（ひとなみにおごれや）
怒りが込められた語呂合わせですね。
アイツ、ケチなんだよなー人並みには奢ってくれよ
おかげで\(\sqrt{3}\)はケチ！という風評被害が…
これも1.73まで覚えておければOKです。
\(\sqrt{4}=2\)なので、\(\sqrt{4}\)は語呂合わせで覚える必要はありません。
ということで、次は\(\sqrt{5}\)いきましょー！
\(\sqrt{5}\)の語呂合わせ
$$\Large{\sqrt{5}=2.2360679\cdots}$$
富士山麓 オウム鳴く（ふじさんろくおうむなく）
富士山とオウムのキレイな絵がパッと浮かんでくる素晴らしい語呂合わせですね。
数学で疲れた心が、富士山の美しい景色とオウムに癒されるようです。
\(\sqrt{5}\)は癒し担当といったところでしょうか。
これも2.23まで覚えておけばOK！
\(\sqrt{6}\)以降の近似値については
あまり活躍しないので、興味がある人だけ覚えておきましょう。
もちろん、覚えておいた方が得なことに間違いはありませんので。
\(\sqrt{6}\)の語呂合わせ
$$\Large{\sqrt{6}=2.449489\cdots}$$
煮よ よく弱く（によよくよわく）
煮よ！
でも弱くね～
アメとムチ！ツンデレ！ってやつですね。
\(\sqrt{7}\)の語呂合わせ
$$\Large{\sqrt{7}=2.64575\cdots}$$
菜に虫いない（なにむしいない）
※菜（な）は\(\sqrt{7}\)のことです。
語呂をよくするために\(\sqrt{7}\)の7を使っています。
ちょっと納得いかない感じがありますが、覚えやすくするためです。
グッと飲み込んでください(^^;
ただ、個人的には虫が苦手なので
数学に虫を登場させちゃうこの語呂合わせは嫌いです…
\(\sqrt{8}\)の語呂合わせ
$$\Large{\sqrt{8}=2.828\cdots}$$
ニヤニヤ（にやにや）
（・∀・）ﾆﾔﾆﾔ
覚えやすくて大好きな語呂合わせですｗ
ただ、\(\sqrt{8}=2\sqrt{2}\)であることを利用すれば
$$\sqrt{8}=2\sqrt{2}$$
$$=2\times 1.414\cdots$$
$$=2.828\cdots$$
というように導けるので、\(\sqrt{2}\)の近似値を覚えておけば\(\sqrt{8}\)もセットで覚えておけますね！
語呂合わせ覚えておくと、こんな場面で役に立つ！
さて、ここまで平方根の値を語呂合わせで
覚える方法について紹介してきましたが、ここで疑問が１つ。
別に近似値なんて覚えなくてよくね？
だってさ、\(\sqrt{2}\)だったら
$$\Large{\sqrt{1}<\sqrt{2}<\sqrt{4}}$$
$$\Large{1<\sqrt{2}<2}$$
だから、だいたい１から2までの値だなって分かるじゃん！
それで十分じゃん。
仰る通りです。
ルートのだいたいの値が分かればOKという問題がほとんどです。
だけど、高校生の問題になると
$$\Large{3-(\sqrt{2}+\sqrt{3})}$$
この計算の答えって正になる？負になる？
という判断が必要になる場面が出てきます。
こういうときに
\(1<\sqrt{2}<2\)、\(1<\sqrt{3}<2\)ということしか分からなければ
答えが正になるか、負になるか判断がつかないんですね。
ともに大体、１くらいだから\(3-(1+1)=3-2>0\)
正になる！と判断すると罠にはまってしまいます。
一方で、語呂合わせでちゃんと近似値を覚えておけば
$$\Large{3-(\sqrt{2}+\sqrt{3})}$$
$$\Large{≒ 3-(1.41+1.73)}$$
$$\Large{=3-3.14<0}$$
このように、計算結果が負になることが判断できました！
答えが正か負なんてどっちでもいいじゃん…って思うんですが
高校数学ではこの正か負が
生か死を分けるくらい大事な材料になることがあるんですね。
こういう場面で本領を発揮する語呂合わせ！
やっぱり覚えておくとお得ですね(^^)
まとめ
お疲れ様でした！
最後に語呂合わせをまとめておきましょう。
平方根の語呂合わせ$$\Large{\sqrt{2}=1.41421356\cdots}$$
一夜一夜に人見頃（ひとよひとよにひとみごろ）
$$\Large{\sqrt{3}=1.7320508\cdots}$$
人並みに奢れや（ひとなみにおごれや）
$$\Large{\sqrt{5}=2.2360679\cdots}$$
富士山麓 オウム鳴く（ふじさんろくおうむなく）
$$\Large{\sqrt{6}=2.449489\cdots}$$
煮よ よく弱く（によよくよわく）
$$\Large{\sqrt{7}=2.64575\cdots}$$
菜に虫いない（なにむしいない）
$$\Large{\sqrt{8}=2.828\cdots}$$
ニヤニヤ（にやにや）
以上！
覚えておくと、ちょっと得する語呂合わせでした。
\(\sqrt{5}\)までは、問題でもよく使うからちゃんと覚えておこうね。
ファイトだー(/・ω・)/
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、以下の内容を無料でお届けします！
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
3−(√2+√3)の正負ですが、以下の計算（中学生の範囲かな？）で比較的簡単に求まります。ほとんどの場面で大体の値が分かればいいものばかりだと思うので、高校生になると…の説明に比べると、直角三角形の斜辺の長さについての感覚を養うための説明の方が良いと思いました。（結局斜辺は何センチなの？という疑問を持つ生徒向けです。）
3と(√2+√3)のどっちが大きいか。
⇔3⋚√2+√3
⇔9⋚5+√2√3 (両辺二乗)
⇔4⋚√2√3
ここで4=√2√2だから4＜√2√3。
したがって3-√2+√3負値。
コメントありがとうございます！
きっと役に立つ生徒さんも多いと思いますので
コメントに表示するという形での紹介になりますが
シェアさせていただきます。
√10の語呂合わせはないんですか？
√10の語呂合わせはちょっと分からないです…ごめんなさい(^^;)
どうしても値を知りたかったら
√10=√2×√5だから
√2と√5の値を用いて
1.41×2.23=3.14…と求めることができますね！