今回は中3で学習する平方根』の単元から
この単元の基礎となる平方根の求め方について学んでいきましょう!
- 平方根ってなんだ?
- ルートってなに?
- 分数や小数の平方根ってどうやって求めるの?
という点について解説していくよ!
では、一緒に勉強していきましょー
今回の記事は、こちらの動画でも解説しています(/・ω・)/

平方根とは
2乗すると\(a\)になる数を\(a\)の平方根といいます。
ちなみに平方とは、2乗を意味する言葉です。
小学生のときには、平方センチメートルなんて言葉が
面積を求めるときには登場したよね!
㎠っていう単位を見ると
㎝が2乗されているから平方センチなんだー!って分かるね
ちょっと余談ですが
3乗すると\(a\)になる数を\(a\)の立方根、または3乗根といいます。
立方という言葉も体積のときに㎤でお世話になったよね。
まぁ、この立方根については高校生で学習するお話なので一旦、置いておきましょう。
では、話を戻して!
4の平方根ってどうなる?ということについて考えてみましょう。
4の平方根というのは、2乗して4になる数のことだから
$$\Large{2^2=4}$$
$$\Large{(-2)^2=4}$$
このように\(2, -2\)が見つかります。
よって、4の平方根は\(+2\)と\(-2\)だということになります。
基本的に平方根は、このように+と-の数がセットで出てきます。
なので、これらをまとめて\(\pm 2\)と表していくようになります。
(これをプラスマイナス2と読みます)
それでは、例題をいくつか
9の平方根は ⇒ \(\pm 3\)
25の平方根は ⇒ \(\pm 5\)
81の平方根は ⇒ \(\pm 9\)
平方根はこのように考えていきます。
平方根の求め方(ルートとは?)
これで平方根はバッチリだぜ!

と思ったあなた…
それでは
5の平方根っていくらになるか分かるかな??
2乗して5になる数だから…
み、見つからないよ

困っちゃうよね。
2乗するとその数になるものなんて
見つからない場合の方が多いです。

平方根を上手く表せないものが多くて困っちゃう…
そこでね!
昔の偉い人たちが
ルート√という記号を使って平方根を表すことで
この問題を解決していくことにしたんですね。
ちなみにルートの記号は
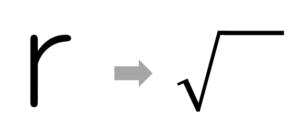
このようにrootの頭文字であるrを変形して作ったと言われてるよ。
つまり、ルートという記号を使えば
2の平方根 ⇒ \(\pm \sqrt{2}\)
3の平方根 ⇒ \(\pm \sqrt{3}\)
4の平方根 ⇒ \(\pm \sqrt{4}=\pm 2\)
5の平方根 ⇒ \(\pm \sqrt{5}\)
こんな感じで平方根を表すことができるようになるんだ!
ただし、4の平方根のように\(\pm 2\)と数が見つかる場合には
ルートは使わない形で表してやりましょう。
平方根のポイント2乗すると\(a\)になる数を\(a\)の平方根といって\(\pm \sqrt{a}\)と表します。
ただし、整数などで表せる平方根はルートを使わない形で表す。
大きい数の平方根は?3桁の数は暗記も必要!
さぁ、ルートという記号を学んだことで
平方根は今度こそバッチリだぜ!
と、いきたいところなんですが
121の平方根は?
んーーっと
ルートを使って
\(\pm \sqrt{121}\)でしょ!!

惜しいっ!
答えは\(\pm11\)となります。
確かめてもらったら分かると思いますが
$$11\times 11=121$$
$$(-11)\times (-11)=121$$
\(\pm 11\)は2乗すると、ちゃんと121になっているよね。
このように
大きい数の平方根というのは
ルートを使って表すべきなのか
それとも2乗になる数が見つかるまで頑張るべきなのか判断がつきにくいよね。
だから
大きい数の平方根を考えていくためには
どの数は、ルートを使わなくても表せるのか
ということを多少は、覚えておく必要があります。
中学で覚えておきたいのは以下の5つ!
$$\Large{11^2=121}$$
$$\Large{12^2=144}$$
$$\Large{13^2=169}$$
$$\Large{14^2=196}$$
$$\Large{15^2=225}$$
この5つは丸暗記してください。
私が指導に当たる際には、必ず暗記してもらっています。
今後も使う場面は多々ありますから、今のうちに覚えるべし!
このことを覚えておけば
121の平方根 ⇒ \(\pm 11\)
144の平方根 ⇒ \(\pm 12\)
169の平方根 ⇒ \(\pm 13\)
196の平方根 ⇒ \(\pm 14\)
225の平方根 ⇒ \(\pm 15\)
このように迷うことなく、平方根を求めることができます。
分数の平方根
次は分数の平方根について考えていきましょう。
\(\displaystyle \frac{9}{16}\)の平方根は?
分数だからといって、特別な考え方をするわけではありません。
分母と分子の数についてそれぞれ考えていけば良いだけです。
今回の場合
分母の16の平方根は\(\pm 4\)
分子の9の平方根は\(\pm 3\)
よって
\(\displaystyle \frac{9}{16}\)の平方根 ⇒ \(\displaystyle \pm\frac{3}{4}\)
となります。
分数の場合には
分母と分子をそれぞれ別々で考えてみると簡単に求めることができますね。

小数の平方根
最後に小数の平方根を考えていきましょう。
\(0.16\)の平方根は?
小数の平方根は間違いやすいので注意です!
答えから言うと
\(0.16\)の平方根 ⇒ \(\pm 0.4\)
となります。
\(\pm 0.04\)としてしまった人は、要注意!
小数はかけ算すると小数点が動いちゃうんでしたね。
だから、\(0.04\)の場合、2乗すると
$$0.04 \times 0.04 =0.0016$$
\(0.0016\)という全然違う数になっちゃいます。
点が動くことを想定して
平方根を考えないといけないので注意が必要です。
そして、小数の平方根で一番気をつけたいのがコレ
\(0.4\)の平方根は?
多くの人が\(\pm 0.2\)と答えてしまうのですが
答えは\(\pm \sqrt{0.4}\)となります。
\(0.2\)だと2乗すると
$$0.2\times 0.2 =0.04$$
となってしまうので、\(0.4\)にはならないよね。
2乗して、\(0.4\)になる数は見つからないのでルートを使って表すことになります。
このように、パッと見に騙されてしまいそうになるので
小数点の位置には細心の注意が必要です。
小数点の位置に不安がある方は
小数点以下の数が偶数なら
0.04の平方根 ⇒ \(\pm 0.2\)
数によっては、ルートを使わずいける可能性がある
小数点以下の数が奇数なら
0.4の平方根 ⇒ \(\pm \sqrt{0.4}\)
ルートが必要!
というように判断してもOKです。
練習問題で理解を深める!
それでは、以上のことをまとめて練習問題に挑戦してみましょう。
問題
次の数の平方根を答えなさい。
(1)\(7\) (2)\(16\)
(3)\(196\) (4)\(\displaystyle \frac{49}{169}\)
(5)\(0.25\) (6)\(0.025\)
これができればテストもバッチリ、追加演習を用意しました!
練習問題はバッチリでしたか??
平方根の単元において、今回の内容が一番の基礎となります。そのため、ここを完璧に仕上げておかないと次にやってくる計算で苦戦することに…
というわけで、家庭学習の補助教材として、動画解説付きの追加演習を10題用意しました!
これを見てくださっている保護者の方は、
「あんたこれやってみなさい!」
と、お子さんに渡していただいて、どれくらい解けているかチェックしてみてください!
できていればホッと一安心、できていなければこの記事を見せてしっかりと復習するように!

「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
【演習課題】ルートの基礎
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れ様でした!
これで平方根の求め方はバッチリですね
次は、ルートを使った計算問題などに進んでいくようになります。
これからどんどんと難しいことも学んでいきますが
まずは今回の基礎部分をしっかりと理解しておくことが大事です。
ちょっとでも不安な部分があれば、記事を振り返って復習しておきましょう!
以上!
ファイトだー(/・ω・)/


















コメントを残す