こんにちは!数スタの小田です。
今回は中3の平方根の単元から
「どんな数をかけたり、割ったりしたら√が整数になる?」
というテーマの問題を解説していきます。
すこし難しいテーマではありますが、
おさえておきたいのはこちらのポイントです!
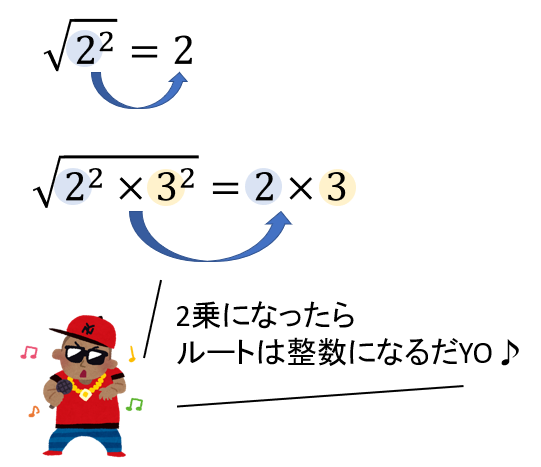
ルートの中身が平方数(2乗の形)になれば整数になるんだ!
ということですね( `ー´)ノ
では、それぞれの問題を解説していきます。
取り上げる問題はこちら
\(\sqrt{24n}\) の値が整数となるような自然数 \(n\)のうち,もっとも小さいものを求めなさい。
\(\frac{\sqrt{28n}}{3}\) を0でない整数にしたい。できるだけ小さい整数\(n\)の値を求めなさい。
\(\sqrt{100-12n}\)が整数となるような自然数\(n\)の値をすべて求めなさい。
\(\sqrt{3a}\)が1けたの自然数になるような自然数\(a\)をすべて求めなさい。

素因数分解の利用(かけ算)
【問題】
\(\sqrt{24n}\) の値が整数となるような自然数 \(n\)のうち,もっとも小さいものを求めなさい。
まずは24を素因数分解して、2乗のペアを作っていきます。

ルートを整数にするためには、中身を2乗の形にする必要があります。
ですが、2と3がそれぞれ2乗になっていません!困った!
ということで、\(n\)のところに2と3を1つずつ入れてあげれば全部を2乗の形にすることができますね。
$$\begin{eqnarray}&&\sqrt{2^2\times 2\times 3\times \color{red}{2\times 3}}\\[5pt]&=&\sqrt{2^2\times 2^2\times 3^2}\\[5pt]&=&2\times 2\times 3=12 \end{eqnarray}$$
こんな感じ!
というわけで、\(n=2\times 3=6\)となります。
答え
$$n=6$$
流れとしては、このように考えていきましょう。
- 素因数分解をして2乗のペアをつくる
- 2乗になれなかった数を見つける
- ②を2乗にするために\(n\)の値を考える
素因数分解の利用(わり算)
【問題】
\(\frac{\sqrt{28n}}{3}\) を0でない整数にしたい。できるだけ小さい整数\(n\)の値を求めなさい。
分数になっているものを整数にするためには次の2点を意識してください。
- ルートの中身を2乗にすること
- 分母を消すこと(整数にしたいので分数はダメ!)
28は素因数分解、分母にある3は分かりやすくするためにルートの形に変換しておきます。
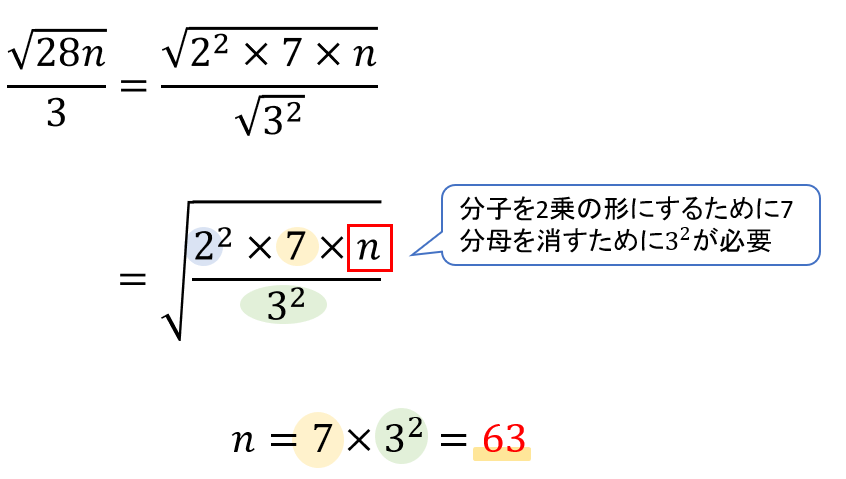
まずは\(\sqrt{28}\)の部分を2乗の形にする必要があるので、7が必要!
さらに分母を約分して消してしまう必要があるので、\(3^2\)が必要!
つまり、\(n=7\times 3^2 =63\)になればいいってことがわかりますね。
答え
$$n=63$$
分数になっているときにはちょっとだけ考えることが増えますが「分母を消す」という意識を持っていれば大丈夫でしょう(^^)
平方数を見つける(ひき算)
【問題】
\(\sqrt{100-12n}\)が整数となるような自然数\(n\)の値をすべて求めなさい。
これまでの問題と違って、ルートの中身がひき算になっていますね。
こういった場合には素因数分解を利用するのではなく、平方数を書き出しながら地道にがんばっていきます…(ファイト!)

まずは、このようにルートの中身がどのような平方数になればいいのかを書き出してください。
その後、方程式を利用しながら\(n\)の値を1つずつ求めていきます。

問題文から\(n\)の値は自然数となっているので、分数になっているものはダメ!
ちゃんと自然数になるものだけを選んでいくと、
\(100-12n=4 ⇒ n=8\)
\(100-12n=16 ⇒ n=7\)
\(100-12n=64 ⇒ n=3\)
このように3つ見つけることができます。
答え
$$n=3,7,8$$
書き出す、方程式を解く…などちょっと面倒に感じるかもしれませんが、慣れてくると頭の中で暗算しながら求めていけるようになります!
たくさん練習あるのみですね^^

発展
【問題】
\(\sqrt{3a}\)が1けたの自然数になるような自然数\(a\)をすべて求めなさい。
ルートを自然数にするためには、中身を2乗の形にする必要があります。
そのため、\(a\)には必ず3の数が含まれることが判断できるはずです。
ですが、それ以外にも次のようなパターンであっても自然数にすることができます。
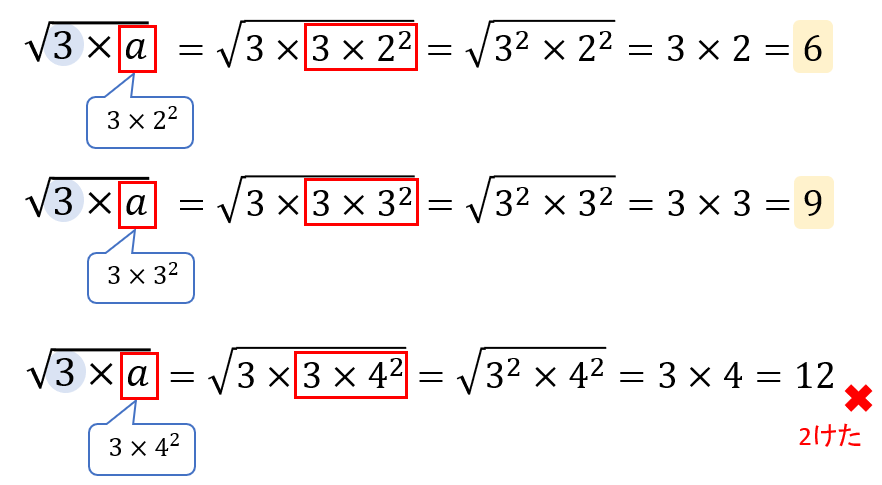
もともとある3を2乗の形にするだけでなく、新たに2乗の数を加えることでも整数にできます。
そうやって考えてみると、
\(a=3, a=3\times 2^2=12, a=3\times 3^2 =27\)
この3つの数を見つけることができます。
答え
$$a=3, 12, 27$$
【追加課題】もっと演習したい方はこちらもどうぞ!
さてさて、ここまでのところで各パターンの解き方、考え方はバッチリだと思います!
ですが、これらがテストに出てきたときに迷わずサクッと解ける自信はありますか…?
「そう言われる自信ないかも…」
という方がほとんどだと思います。(まだ習ったばかりだもんね)
なので!
しっかりと理解を定着させて、テストに向けての自信をつけるための演習課題を用意しました!!
追加演習をやってテストの点数をUPさせたい方には、課題&動画解説をメールで送らせてもらっています。

「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れさまでした!
ちょっと発展的な内容でしたが、ちゃんと理解できましたか??
どの問題においてもポイントは「中身を2乗にする」ことですね!
このタイプの問題は、入試によく出題されるので必ず解けるようにしておいてくださいね(‘◇’)ゞ


















コメントを残す