【平方根】a√b の形に変形するやり方とは？問題を使って徹底解説！

今回は『平方根』の単元から

ルートを\(a\sqrt{b}\)の形にする方法を解説していくよ！

シンプルな変形から

$$\Large{\displaystyle \sqrt{24}}$$

このような数の大きなもの

$$\Large{\sqrt{336}}$$

分数のもの

$$\Large{\sqrt{\frac{5}{16}}}$$

$$\Large{\frac{\sqrt{12}}{4}}$$

まで徹底解説していきます！

今回の記事は、こちらの動画でも解説しています(/・ω・)/

平方根変形の基本

まず、平方根の形を変形していく上で

必ず覚えておきたい基礎がこちら

正の数の2乗になっているとルートの外に出すことができる

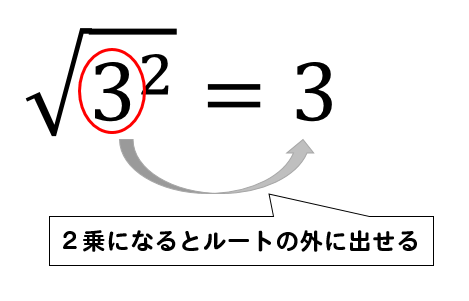
このようにルートの中に正の数の２乗になっているモノがあれば

ルートの外に出すことができます。

このように２乗になるモノが複数個あったり

２乗にならないモノが混じっていても

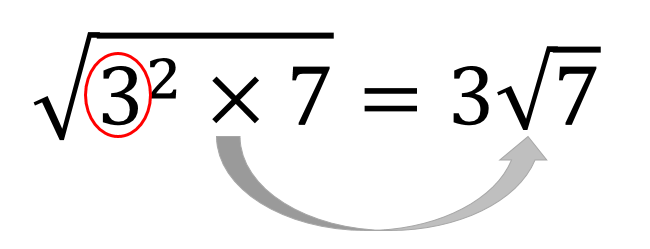
同様に変形することができます。

つまり

変形したいルートの中身に

２乗になる数がどれだけあるか？を見極めることができれば

簡単に\(a\sqrt{b}\)の形に変形することができます。

それでは

２乗になる数はどうやって見つければ良いのか？

素因数分解を使うパターン

ルートの中に、２乗の数がどれだけあるかを見つける方法の一つとして『素因数分解』を利用する方法があります。

例えば\(\sqrt{45}\)を変形して\(a\sqrt{b}\)の形にしたい場合

45を素因数分解してやります。

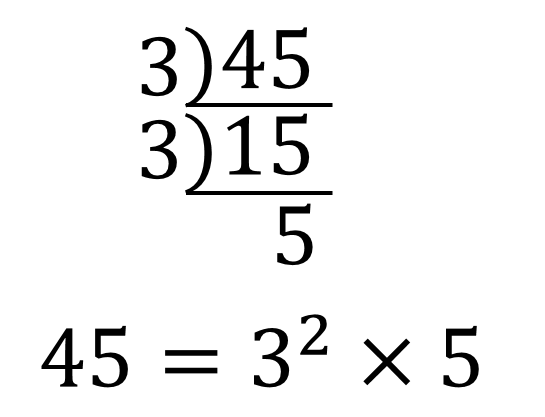
すると45には3の2乗が含まれていることがわかります。

よって

$$\Large{\sqrt{\mathstrut 45}=\sqrt{\mathstrut 3^2\times 5}}$$

$$\Large{=3\sqrt{\mathstrut 5}}$$

と、変形してやることができます。

ちょっと手間ではありますが

素因数分解を利用することで

２乗になっている数を簡単に見つけることができました。

ただし！

素因数分解を利用して２乗を見つける方法では

ちょっと気をつけたいことがあります。

336を素因数分解すると

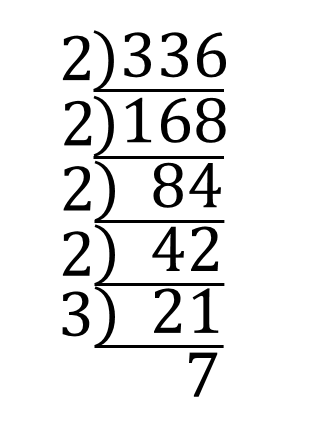
$$\Large{336=2^4\times 3\times 7}$$

となるのですが

平方根の変形では２乗になるパーツを見つけたいだけなので

\(2^4\)は崩してやって

$$\Large{336=2^2\times2^2\times 3\times 7}$$

としてやりましょう。

すると

$$\Large{\sqrt{\mathstrut 336}=\sqrt{\mathstrut 2^2\times2^2\times 3\times 7}}$$

$$\Large{=2\times2\sqrt{\mathstrut 3\times 7}}$$

$$\Large{=4\sqrt{\mathstrut 21}}$$

となります。

大きな数を素因数分解するときには、気を付けてくださいね。

平方数の積を作るパターン

上では、素因数分解を使って

２乗になるパーツを見つけるという方法を紹介しました。

でも、正直…

素因数分解って

めんどうじゃなーーーい？？

というわけで

ちょっと上級者向けではありますが

平方数を使って考える方法を紹介します。

つまり、これらの数の積で表すことができれば

その数は、２乗のパーツを含むことがわかります。

例えば

$$\Large{\sqrt{\mathstrut 24}=\sqrt{\mathstrut 4\times 6}}$$

24は4という平方数を使って積の形で表すことができます。

\(4=2^2\)になるので

$$\Large{\sqrt{\mathstrut 24}=2\sqrt{\mathstrut 6}}$$

となります。

このように

２乗となる平方数を覚えておけば

これらの数を使って積の形で表すことができないか考えます。

平方数を使って表すことができれば

ルートの外に出してやることができます。

いくつか例を挙げておきます。

たくさん問題をこなして慣れてくれば

素因数分解を使ってやるよりも楽にできるようになるはずです(^^)

それでは、問題演習を通して理解を深めていきましょう。

演習問題で理解を深める！

（1）の答え

48を素因数分解してやると

\(\Large{48=2^4\times 3}\)となります。

２乗がどれくらいあるかを知りたいので４乗は

\(\Large{48=2^2\times 2^2\times 3}\)というように変形してやります。

よって

$$\Large{\sqrt{48}=\sqrt{2^2\times 2^2\times 3}}$$

$$\Large{=2\times 2\sqrt{3}}$$

$$\Large{=4\sqrt{3}}$$

16という平方数を使って考えると

$$\Large{\sqrt{48}=\sqrt{16\times 3}}$$

$$\Large{=4\sqrt{3}}$$

こんな感じで変形していくこともできます。

（2）の答え

588を素因数分解してやると

\(\Large{588=2^2\times 3\times 7^2}\)となります。

よって

$$\Large{\sqrt{588}=\sqrt{2^2\times 3\times 7^2}}$$

$$\Large{=2\times 7\sqrt{3}}$$

$$\Large{=14\sqrt{3}}$$

となります。

このように大きい数を変形する場合には

平方数を利用して考えるのは難しいですね。

素因数分解で考えていきましょう。

（3）の答え

ルートを分母、分子それぞれにわけてやります

$$\Large{\sqrt{\frac{3}{25}}=\frac{\sqrt{3}}{\sqrt{25}}}$$

$$\Large{=\frac{\sqrt{3}}{5}}$$

そうすると、このように変形することができます。

（4）の答え

分数ではありますが

気にすることなく分子のルートを変形していきましょう。

$$\Large{\frac{\sqrt{12}}{3}=\frac{\sqrt{2^2\times 3}}{3}}$$

$$\Large{=\frac{2\sqrt{3}}{3}}$$

となります。

時間足りない…を防ぐために追加演習で計算力を鍛えよう！

さて、ここまでのところでルートの変形はバッチリかな？

あとはたくさんの問題にチャレンジして素早く、正確に解けるようにしていきましょう！

ここを練習しておかないと、テストのときに「やり方はわかっていたのに、時間が足りなかった…」という悲しいことになっちゃいます( ;∀;)

なので、この記事を読んでくれている方が「サクサク解いて満点ゲット～♪」となるように、追加演習を用意しました！

この問題を解いて、テストの点数アップを達成してくださいね＾＾

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

a√bの形に変形する方法　まとめ

お疲れ様でした！

\(a\sqrt{b}\)の形に変形する方法を練習してきました。

変形のポイントは

２乗を見つけて、外に出す。

ということでしたね。

２乗になる数を見つけるためには

素因数分解を利用するパターンと

平方数を利用するパターンがありました。

慣れるまでは素因数分解が楽だとは思いますが

数学の得意な人のほとんどは、平方数を利用するパターンを

頭の中で計算してスラスラ解くことができています。

素因数分解でのやり方を完全にマスターした人は

平方数を利用するパターンにも挑戦してみましょう！