【中3】式の計算の利用～円、正方形の図形の証明をイチから～

こんにちは！数スタの小田です。

今回は中3で学習する式の計算の利用から

「円、正方形の図形に関する証明」を解説していきます。

取り上げるのは、こういった図形の問題です。

難しそうに見える問題だけど、手順を覚えてしまえば簡単に解くことができるようになります！

というわけで、それぞれの問題についてみていきましょう。

今回の内容はこちらの動画でも解説しています。動画でサクッと理解しておきましょう！

式の計算の利用

この単元の証明では「\(S=al\)となることを証明しなさい」というのが一般的です。

この証明をするには以下の手順で取り組んでいきましょう。

正方形の図形による証明

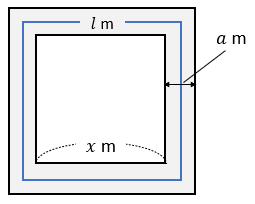
下の図のような2つの正方形にはさまれた幅 \(a\) mの道がある。この道の面積を\(S\)㎡，道の真ん中を通る線の長さを\( l \) mとするとき，\(S=al \)となることを証明しなさい。

手順に沿って、まずはＳ（道の面積）を文字で表していきましょう。

道の面積を表すためには、

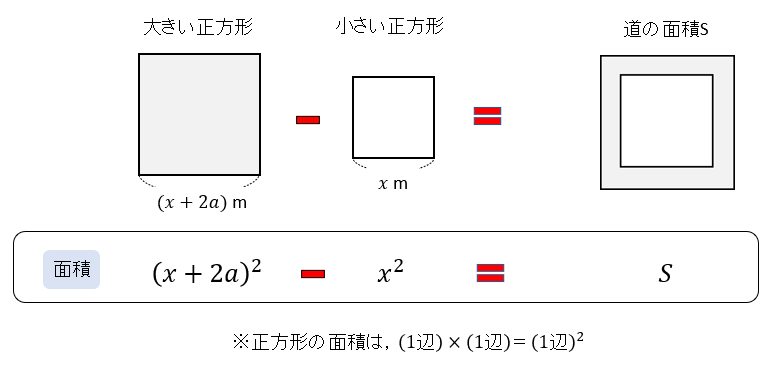
このように大きな正方形から小さい正方形を取り除いて考えましょう。

このとき、大きい正方形の1辺の長さは \((x+2a)\)mになることもポイントですね。

あとはこれを計算していくと、

$$\begin{eqnarray}S&=&(x^2+4ax+4a^2)-x^2\\[5pt]&=&\color{red}{4ax+4a^2\cdots①} \end{eqnarray}$$

\(S\)が表せたら、次は\(al\)の式を作るために \(l\) を文字で表していきましょう。

次の図のように、\(l\)は1辺が\((x+a)\)mの正方形の周の長さです。

よって、\(l\)の長さは\((x+a)\)を4つ分あわせたものだから

\(l=(x+a)\times 4=(4x+4a)m\) と表すことができます。

\(l\) が道の真ん中を通っているので、道幅の半分である \(\frac{a}{2}\)mという値を用いるのが、慣れるまではちょっと難しく感じるかもしれませんね(^^;)

ですが、今回の単元では道の真ん中を通るような図形を用いることが多いので、がんばって慣れていきましょう！

そして、\(l\)が表せたところで\(al\) を文字で表していきましょう。

$$\begin{eqnarray}al&=&a(4x+4a)\\[5pt]&=&\color{red}{4ax+4a^2\cdots②} \end{eqnarray}$$

すると、①②より

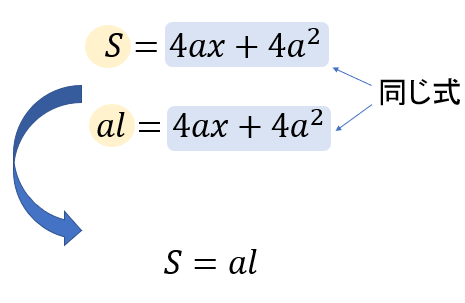
これで証明完了となります！

\(S\)を文字で表す。

\(al\)を文字で表す。

それぞれが同じ式になったから、\(S\)と\(al\)は同じだね！

この流れで証明が完了となります。

証明問題ではありますが、やっていることはただの計算って感じだね(^^)

次の円についても同じ流れで解いていくことができます。

円の図形による証明

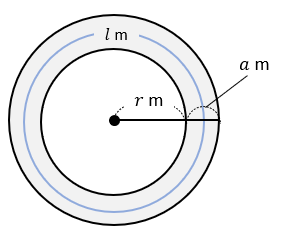
半径\(r\) mの円の周囲に，幅\(a\) mの道がある。この道の面積を\(S\) ㎡，道の真ん中を通る円周の長さを\(l\) mとするとき，\(S=al\) であることを証明しなさい。

まずは、大きな円から小さい円を取り除いて道の面積Sを求めましょう。

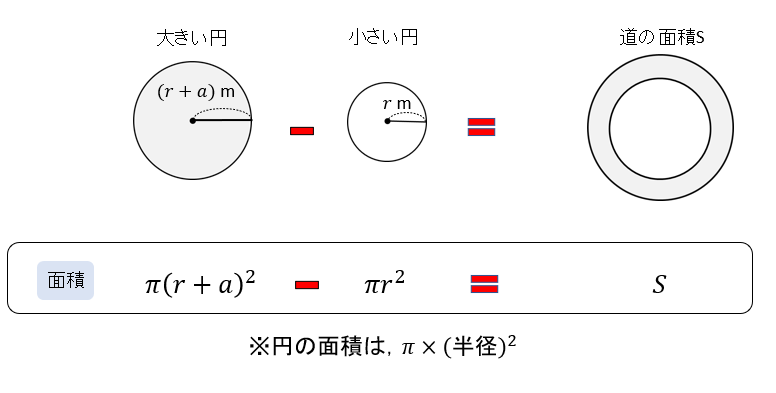
今回は円なので、半径の大きさに注目しながら面積を求めてくださいね。

円の面積を忘れていた人は…喝だッ！

しっかりと思い出しておいてくださいね(-_-)/

これを計算していくと、

$$\begin{eqnarray}S&=&\pi(r^2+2ar+a^2)-\pi r^2\\[5pt]&=&\pi r^2+2\pi ar+\pi a^2-\pi r^2\\[5pt]&=&\color{red}{2\pi ar+\pi a^2\cdots①} \end{eqnarray}$$

\(S\)が表せたら、次は\(al\)の式を作るために \(l\) を文字で表していきましょう。

次の図のように、\(l\)は半径が\(\left( x+\frac{a}{2} \right) \)mの円周の長さです。

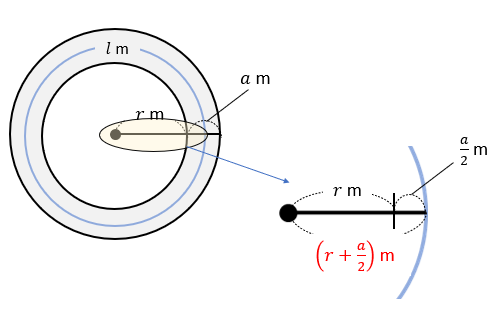
道の真ん中を通っているので、\(\frac{a}{2}\)という値を使いましょう。

円周の長さは、\(2\times \pi \times (半径)\)なので、

$$\begin{eqnarray}l&=&2\times \pi \times \left( r+\frac{a}{2}\right) \\[5pt]&=&2\pi r+\pi a \end{eqnarray}$$

$$\begin{eqnarray}al&=&a(2\pi r+\pi a)\\[5pt]&=&\color{red}{2\pi ar+\pi a^2\cdots②} \end{eqnarray}$$

すると、①②より

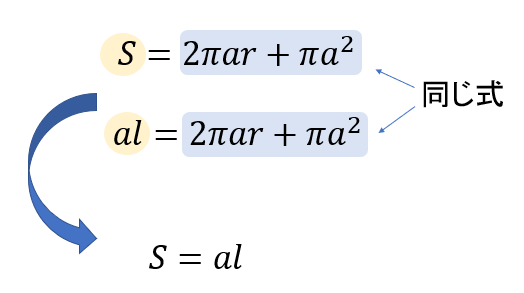
【特典】書き込み式のプリントで「できる」を目指す！

さて、ここまでのところで証明の流れはバッチリですかね！

今回の内容は中3の学生さんから質問いただくことが多く、その度に個別指導で教えてきました。ありがたいことに「なるほど、わかりました！」と、すぐに説明を理解してくれるのですが…

「じゃ、イチから自分で証明を書いてみましょうか！」

と言うと、また手が止まってしまう…ということが多発(^^;)

つまり、解説を聞いて納得はできたけど、自分でイチから解くまでの理解はできていない…ってことですね。このままではテストで得点することは難しいです＞＜

というわけで、しっかりとイチから証明が書けるようになるために「模写」をしてもらいました。僕の解説を見ながらでいいので、実際に手を動かして証明を書いてみるってことです！

そうすると、あら不思議！！

テストでもしっかりと証明がかけるようになって、ちゃんと点数アップするようになりました。説明を聞いてインプットされた情報を、手を動かしてアウトプットしたことで理解の定着につながったんですね＾＾

今回のような証明問題は、解説を読んだだけで終わらせてしまう人が多いですが、それは要注意！しっかりと手を動かして、「わかる⇒できる」まで引き上げてください！

というわけで！

今回の追加特典では、書き込み式でスラスラ演習できる証明のプリントを用意しました。これを使って、イチからでも完璧な答案がつくれるように練習しておきましょう(‘ω’)ノ

この記事では取り上げられなかった「〇〇の倍数」についての演習も入れているので、あわせて活用してみてください＾＾

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れさまでした！

証明の流れは理解できましたか？？

やっていることは、文字を使って面積や長さを表しているだけですよね＾＾

どこの辺、長さに注目すればいいのか知っておけば簡単に解けるようになります。

あとは、たくさん練習しておいてくださいね！