今回は中3で学習する二次方程式の単元から、
「どの解き方をすればいい?見分けポイントを紹介!」
ということで解説していきます。
二次方程式では基本的に次の3つの解き方を活用します。
- 平方根の考えを利用した解き方
- 因数分解を利用した解き方
- 解の公式を利用した解き方
そこで、今回は次の問題を使いながら解き方の見分け方について解説します(^O^)/
最後には演習問題も用意しているので挑戦してみてください。
次の二次方程式を解きなさい。
(1)\(16x^2=25\)
(2)\(x^2-8x=-3\)
(3)\(2x^2=3x\)
(4)\((x+4)(x-4)=3x-6\)
今回の内容については、こちらの動画でも解説しています。
サクッと理解したい方はこちらをどうぞ(‘◇’)ゞ

二次方程式の解き方を見分けるポイント!
どの解き方でやればいいのかを判断するには、次のポイントをおさえておきましょう!
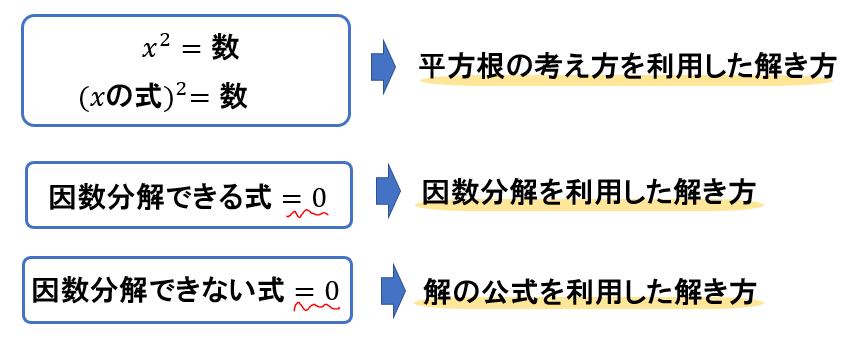
\(x\)の2乗、\(x\)のかたまりの2乗の他に\(x\)がついた項がなく、数しかないときには「平方根」
平方根の解き方ができない場合において、すべての項を左辺に移項し「\(=0\)」の形をつくったとき、左辺が因数分解できる形であれば「因数分解」、そうでなければ「解の公式」
このように見分けていきましょう!
解き方をチェック
(1)の解き方
次の二次方程式を解きなさい。
(1)\(16x^2=25\)
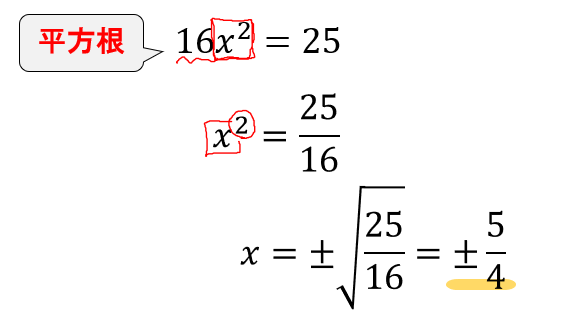
これは式を見たときに、\(16x^2\)以外に\(x\)のついた項がなく、25という数しかありませんね。
なので、平方根の解き方が利用できると判断します。
(2)の解き方
次の二次方程式を解きなさい。
(2)\(x^2-8x=-3\)
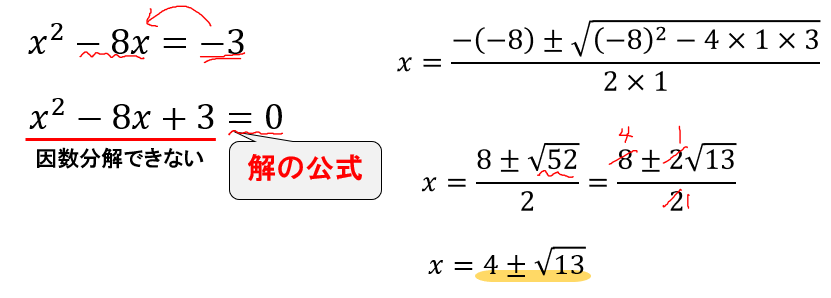
\(x^2\)の他には\(-8x\)という\(x\)のついた項があります。
そのため、今回は平方根の解き方ができない…と判断できます。
すると、次は項をすべて左辺に集め「\(=0\)」の形をつくりましょう。
その上で、左辺にある式が因数分解できるかどうかをチェックします。
すると、今回は因数分解することができないので「解の公式」を利用することになります。
(3)の解き方
次の二次方程式を解きなさい。
(3)\(2x^2=3x\)
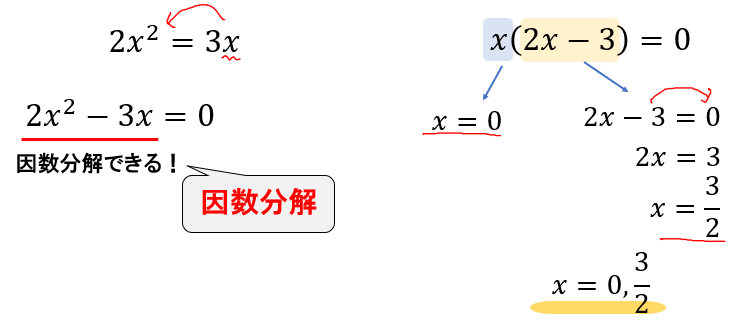
平方根の解き方をしたくなる見た目ですが、惑わされないでくださいね!
\(2x^2\)のほかに、\(x\)のついた\(3x\)という項があるので平方根の解き方は使えませんね。
そこで左辺に移項して、因数分解できるかどうかをチェックしましょう。
すると、共通因数でくくれるので「因数分解」を利用した解き方になります。
(4)の解き方
次の二次方程式を解きなさい。
(4)\((x+4)(x-4)=3x-6\)

見た目がゴチャっとしていますが、まずは式を展開して左辺に集めていきましょう。
すると、左辺は因数分解できる形になっているので「因数分解」を利用して解けばOKです。
流れとしてはこんな感じで見ていくとイイですね!
- \(x\)の項をチェックして平方根の解き方ができるか判断する、
- 左辺に項を集めて因数分解できるか判断する。
- 因数分解できないなら解の公式を使う。
では、解き方の見分けポイントをおさえた上で、次の演習にチャレンジしてみましょう!
演習問題にチャレンジしてみよう!
次の二次方程式を解きなさい。
(1)\(x^2-4x=0\)
(2)\((x-1)^2=15\)
(3)\(2x^2-7x+4=0\)
(4)\((x-2)(x+2)=3x\)
(5)\((x+1)(x-6)+9=0\)

まとめ&ランダム入試プリント!
お疲れ様でした!
二次方程式にはいろんな解き方があるので、それらを使い分けていくのは大変ですよね(^^;)
習得のポイントは「とにかくたくさん演習する」です!
この式がきたらこう解く!といった感覚を体に覚え込ませていくことが大事です。
というわけで、二次方程式の計算を極めるために「入試から抜粋した二次方程式のランダム演習プリント」を作りました!
ここで取り上げている問題はこちら!

いろんな解き方がランダムになるように並べています。
これらを迷うことなくスラスラ解けたら二次方程式の計算はもう完璧ですね^^
この追加演習をやってテストの点数をUPさせたい方には、課題プリント&解説をメールで送らせてもらっています。
【演習課題】二次方程式(ランダム)
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^





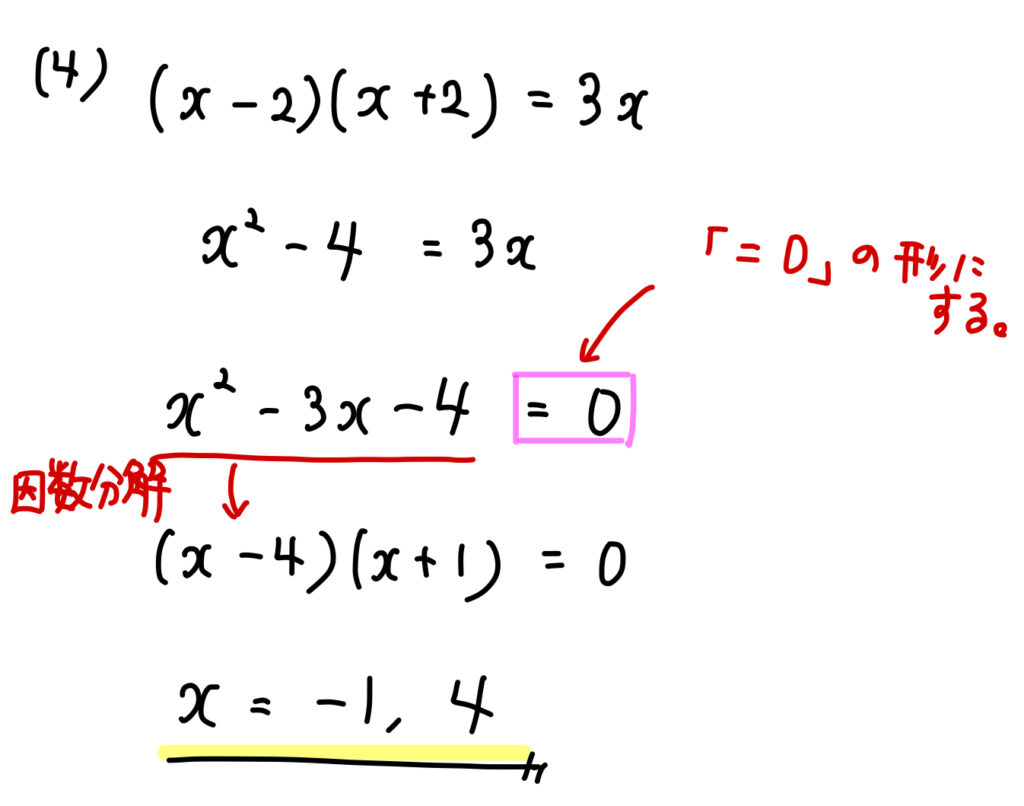














コメントを残す