【ルートの分数計算】問題解説で完全マスターだ！

ルートの分数計算って…

マジ複雑！

できることなら見たくもない！

って感じですよねｗ

だけど、そうも言ってられないので

この記事を通して克服していきましょう。

というわけで、今回は複雑そうなルートの分数計算をいくつかピックアップしました。

これらの解き方を丁寧に解説をつけていくので

みんな！

ルートの分数計算をマスターしちゃおうぜ★

今回の記事はこちらの動画でも解説しています(/・ω・)/

（1）有理化をしっかりとね

分母にルートがあれば有理化！

ルートの中が大きいときには簡単にする！

ルートの計算においては、この2つが鉄則ですね(^^)

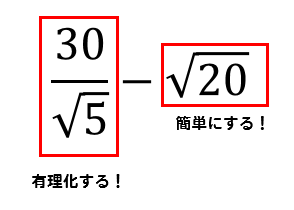
$$\frac{30}{\sqrt{5}}-\sqrt{20}$$

$$=\frac{30\times \sqrt{5}}{\sqrt{5}\times \sqrt{5}}-2\sqrt{5}$$

$$=\frac{30\sqrt{5}}{5}-2\sqrt{5}$$

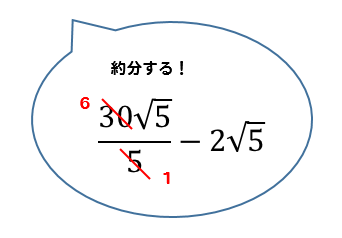
$$=6\sqrt{5}-2\sqrt{5}$$

$$=4\sqrt{5}$$

しっかりと有理化ができれば

あとは簡単ですね(^^)

（2）通分が必要だ

まずは有理化、そして掛け算の計算をやっていきましょう。

$$\sqrt{8}\times \sqrt{3}-\frac{2}{\sqrt{6}}$$

$$=\sqrt{24}-\frac{2\times \sqrt{6}}{\sqrt{6}\times \sqrt{6}}$$

$$=2\sqrt{6}-\frac{2\sqrt{6}}{6}$$

$$=2\sqrt{6}-\frac{\sqrt{6}}{3}$$

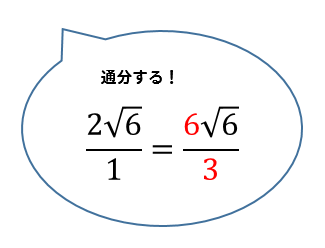
$$=\frac{6\sqrt{6}}{3}-\frac{\sqrt{6}}{3}$$

$$=\frac{5\sqrt{6}}{3}$$

今回の問題のように通分が必要になる場合もあります。

だけど、１つずつ丁寧にやっていけば大丈夫だね(^^)

（3）分数の上にたくさん…

かなり複雑な形だけど、やっていくことは一緒だよ！

まずは有理化、そして展開だね。

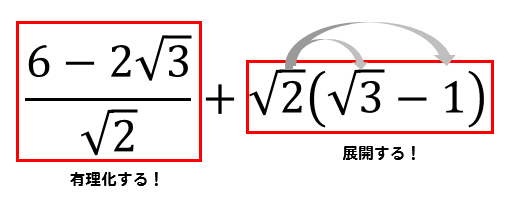
$$\frac{6-2\sqrt{3}}{\sqrt{2}}+\sqrt{2}(\sqrt{3}-1)$$

$$=\frac{(6-2\sqrt{3})\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}+\sqrt{6}-\sqrt{2}$$

$$=\frac{6\sqrt{2}-2\sqrt{6}}{2}+\sqrt{6}-\sqrt{2}$$

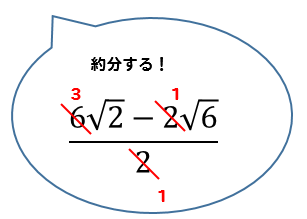
$$=3\sqrt{2}-\sqrt{6}+\sqrt{6}-\sqrt{2}$$

$$=2\sqrt{2}$$

分数の上にたくさん乗っていても

やり方は一緒だ！

だけど、計算ミスしやすくなるから途中式をしっかりと書くようにしようね。

（4）有理化⇒通分の流れ

分母にルートがあるので有理化をしていきましょう。

有理化を簡単にするため、\(\sqrt{8}\)と\(\sqrt{50}\)は簡単な形に変形しておきます。

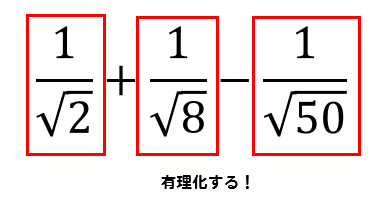
$$\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{8}}-\frac{1}{\sqrt{50}}$$

$$=\frac{1}{\sqrt{2}}+\frac{1}{2\sqrt{2}}-\frac{1}{5\sqrt{2}}$$

$$=\frac{1\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}+\frac{1\times \sqrt{2}}{2\sqrt{2}\times \sqrt{2}}-\frac{1\times \sqrt{2}}{5\sqrt{2}\times \sqrt{2}}$$

$$=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{4}-\frac{\sqrt{2}}{10}$$

$$=\frac{10\sqrt{2}}{20}+\frac{5\sqrt{2}}{20}-\frac{2\sqrt{2}}{20}$$

$$=\frac{10\sqrt{2}+5\sqrt{2}-2\sqrt{2}}{20}$$

$$=\frac{13\sqrt{2}}{20}$$

（5）高校バージョンの有理化

これは高校生レベルの問題になります。

分母にルートがあるので、有理化をしていきますが

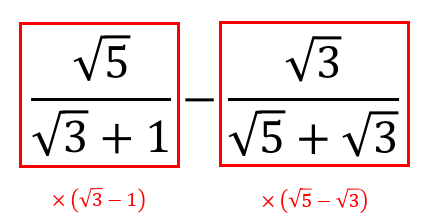
このような式を掛けて有理化していきましょう。

$$\frac{\sqrt{5}}{\sqrt{3}+1}-\frac{\sqrt{3}}{\sqrt{5}+\sqrt{3}}$$

$$=\frac{\sqrt{5}(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}-\frac{\sqrt{3}(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$$

$$=\frac{\sqrt{15}-\sqrt{5}}{3-1}-\frac{\sqrt{15}-3}{5-3}$$

$$=\frac{\sqrt{15}-\sqrt{5}}{2}-\frac{\sqrt{15}-3}{2}$$

$$=\frac{(\sqrt{15}-\sqrt{5})-(\sqrt{15}-3)}{2}$$

$$=\frac{\sqrt{15}-\sqrt{5}-\sqrt{15}+3}{2}$$

$$=\frac{3-\sqrt{5}}{2}$$

【特典課題】ここまで解けたら分数計算は完璧です！

さて、それぞれの演習はバッチリでしたか？

これだけやっとけばテストも安心だね！と言いたいところなんですが…

分数計算はややこしいだけあって、テストでミスをする人が続出します(^^;)

なので、テストでミスをしないためにたくさんの練習をこなしておく必要があります！

というわけで、今回はこの記事を最後まで取り組んでくれた方へのお礼として特典課題を用意しました(‘ω’)ノ

この課題にはルートの分数計算を10題収録しています。難しいモノもありますが、これらが解けるようになっていればテストは大丈夫でしょう＾＾

最後のもうひと踏ん張りです！がんばってください！！

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

ルートの分数計算まとめ

お疲れ様でした！

ルートの分数計算のポイントは

有理化＆通分だね！

たくさん問題演習をして理解を深めていこう

ファイトだ(/・ω・)/