【高校入試】連立方程式の文章問題に挑戦！～第1回～

今回挑戦する入試問題は『連立方程式の文章問題』です。

連立方程式の文章問題は、どこの高校でも出題される頻出問題ですね！

たくさん練習して、解法を身につけていきましょう。

問題の考え方！

まずは、博物館の料金システムを理解しておきましょう。

10人以上で入館すれば、割引が適用されるということですね。

団体で入場すれば割引されるということなので

パーセントの表し方も確認しておきましょう。

詳しくは、こちらの記事で解説しています。

【文字式】割合（パーセント）の問題をわかりやすく解く方法！

今回の問題では

個人料金で入館した場合の合計金額と

団体料金で入館した場合の合計金額が与えられています。

ここからそれぞれの式を作って連立方程式にして解いていきます。

団体料金では、割引後の料金を文字を使って表すことができるかどうかがポイントとなりますね。

問題の答えと解説！

（1）の解説

大人2人と中学生3人が入館したところ、個人料金となり、合計が3400円になった。

という部分から式を1つ作ります。

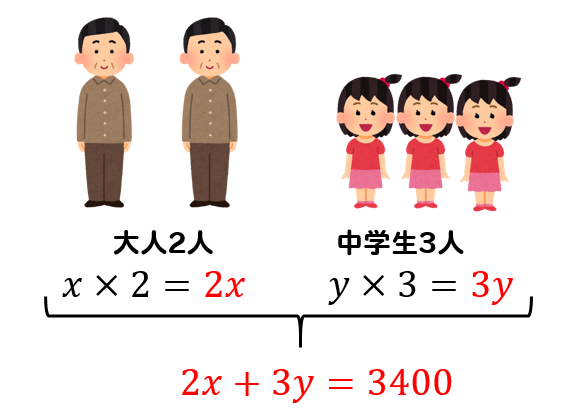
次に団体料金が適用される場合の式を作りましょう。

まず、団体料金を文字で表しておきます。

大人は20％引きだから

中学生は10％引きだから

それぞれこのように表すことができます。

次に

大人10人と中学生30人が入館したところ、団体料金となり、合計が21100円になった。

という部分から

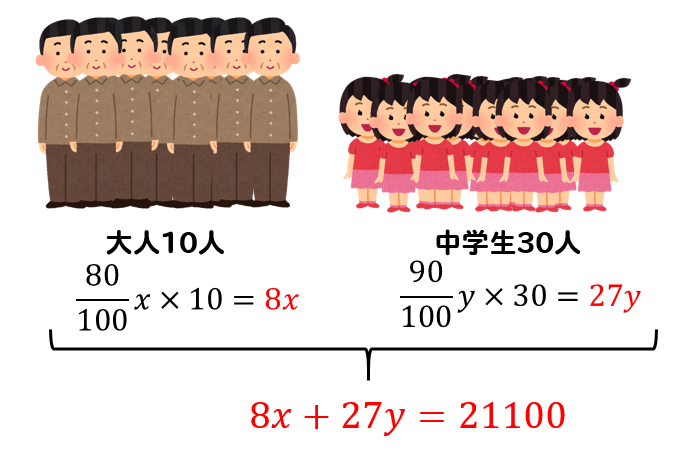
以上より、連立方程式は

$$\large{\begin{eqnarray} \left\{ \begin{array}{l}2x+3y=3400 \\8x+27y=21100 \end{array} \right. \end{eqnarray}}$$

となります。

（2）の解説！

（1）で作った連立方程式を解いていきましょう。

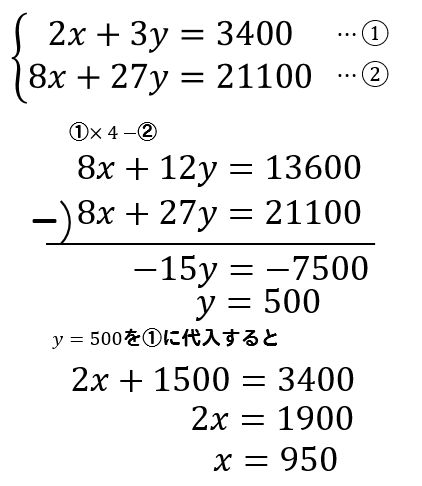
よって

大人の個人料金は950円

中学生の個人料金は500円となります。

まとめ

お疲れ様でした！

今回の問題では、しっかりと文章を読んで料金システムを理解すること。

そして、パーセントの表し方を理解していること。

この2点がポイントでしたね。

入試に出題される文章問題は、難しく見せようと文章が長くなっていることが多いです。

落ち着いて文章を読めば、難しいことは何も書いていないと理解できるはずです。

こんな感じで第１回はおわりっ！

【高校入試】連立方程式の文章問題（速さ）に挑戦！～第２回～