今回は数学Bで学習する『ベクトル』の単元から
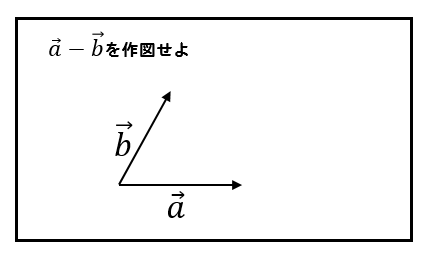
引き算の作図について解説していきます!
足し算は分かるけど
引き算はわからない!
という方は多いようです。
ですが、コツが分かれば簡単です(^^)
それでは、解説していくぞー!
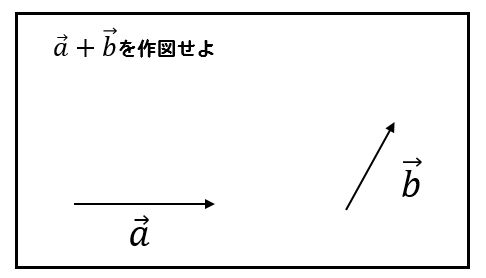
ベクトルの足し算について確認!
ベクトルの引き算を考える前に、足し算について確認しておきましょう。
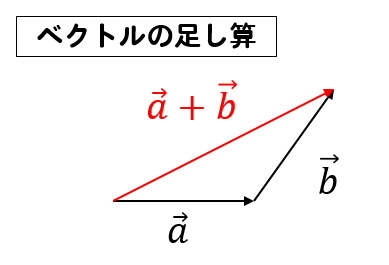
ベクトルの足し算とは、こんな感じでしたね(^^)
分かっている人も多いかもしれませんが、考え方を簡単に解説しておきますね。
足し算をする場合、\(\vec{a}\)の始点と\(\vec{b}\)の終点をつなげます。
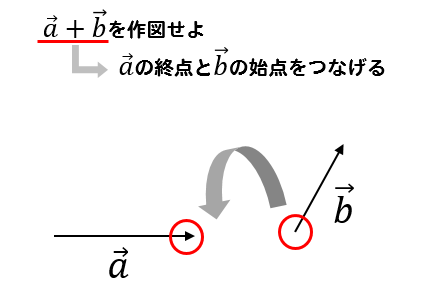
そして、ベクトルがつながったところで
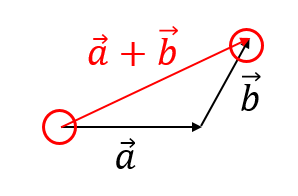
始点と終点を結んでやると足し算の作図が完成します。
引き算もこの考え方を使っていくからね!
逆ベクトルについて
ベクトルの引き算を考えるうえで
逆ベクトルというものを知っておくと便利です。
逆ベクトルとは、名前の通り
逆のベクトルのことです。
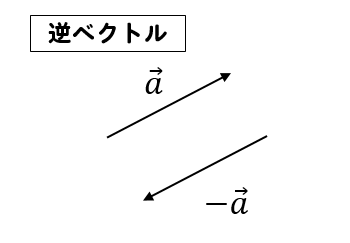
大きさが等しく、向きが反対であるベクトルのことを逆ベクトルといい、マイナスを使って表します。
引き算の作図はこれでバッチリ!
それでは、ベクトルの引き算について解説していきます。

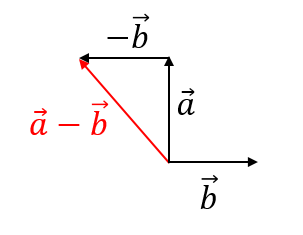
引き算を考える場合、逆ベクトルを使って
$$\Large{\vec{a}-\vec{b}=\vec{a}+(\vec{-b})}$$
というように考えていくと分かりやすくなります。
つまり、\(\vec{a}\)と\(\vec{-b}\)の足し算の作図を考えれば良いということですね。
まずは、向きを反対にした\(\vec{-b}\)を作ります。
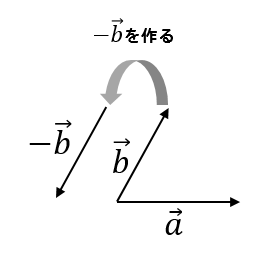
そして、\(\vec{a}\)の終点と\(\vec{-b}\)の始点をつなげて引き算のベクトルを完成させます。
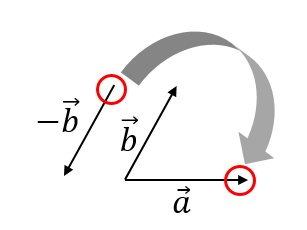
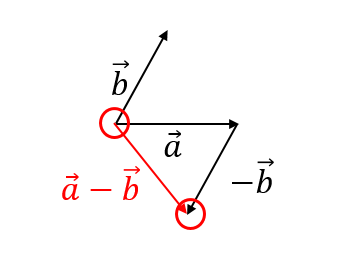
これで完成!!
ベクトルの引き算では、逆ベクトルの足し算だ!
というように考えると分かりやすくなりますね(^^)
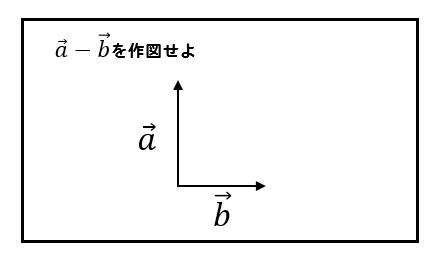
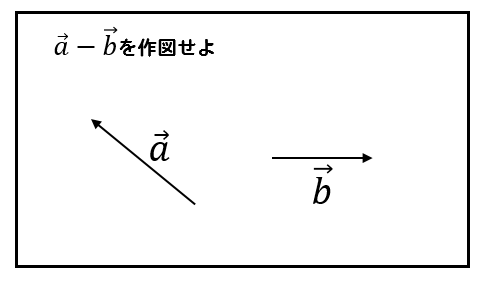
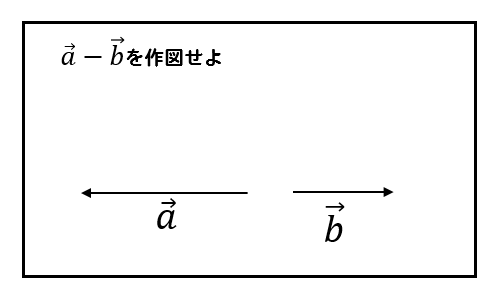
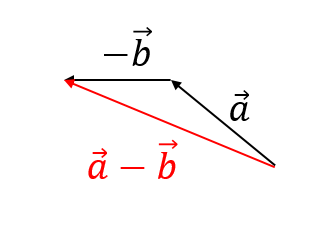
それでは、いくつか練習問題を用意しました。
理解を深めていきましょう!
練習問題に挑戦
ベクトル引き算の作図 まとめ
お疲れ様でした!
ベクトルの引き算は、逆ベクトルを使って足し算と同じように考えることができます。
足し算の作図は理解できている人が多いです。
だから、引き算も足し算と同じように考えることで理解が深まりますね(^^)
あとは、たくさん練習問題を解いて身につけていきましょう!
ファイトだー(/・ω・)/


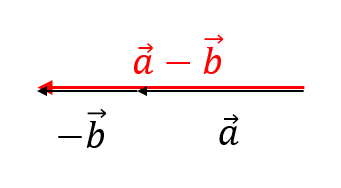
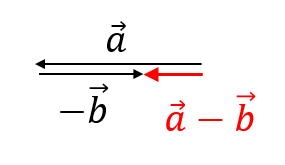










コメントを残す