今回の記事では、おうぎ形の応用問題を扱います。
「影の部分の面積、周の長さの求め方」
について考えてみましょう。
今回取り上げる問題はこちら！
【問題】
次の図は、おうぎ形や正方形を組み合わせたものである。影の部分の面積と周の長さをそれぞれ求めなさい。
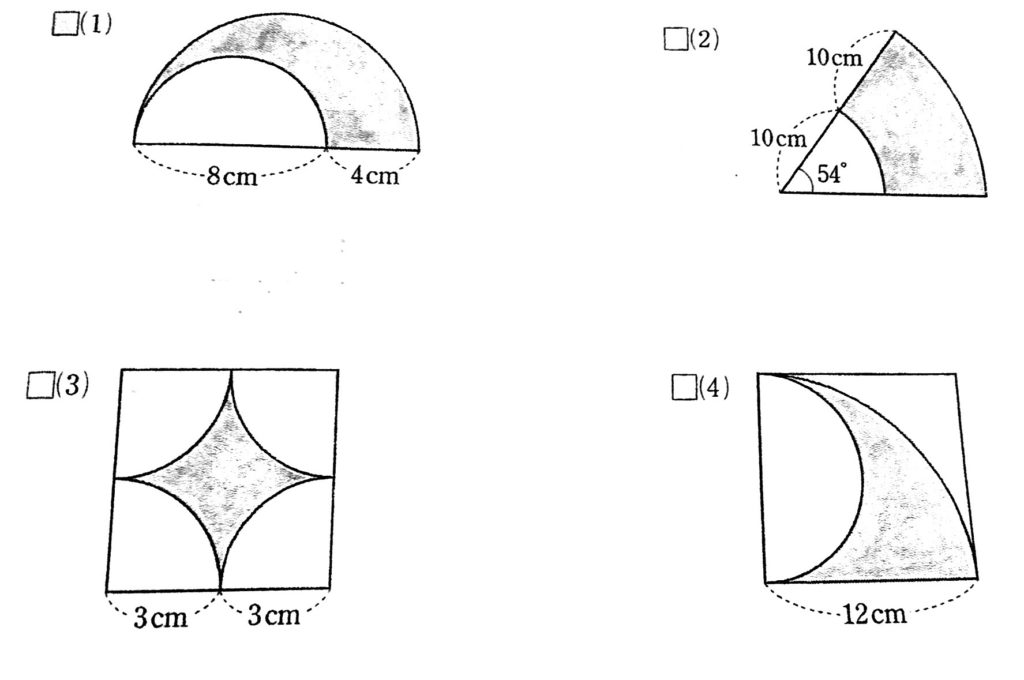
(5)
それぞれの図形の見方、考え方について学んでいきましょう！
おうぎ形の公式って何だっけ？
という方は、まずこちらの記事で復習しておいてね！
Contents
影の部分の面積、周の長さ（1）の解説
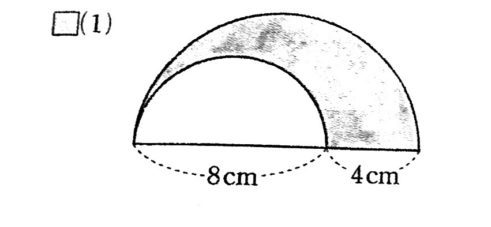
面積を求める場合には、大きな半円と小さな半円に分けて考えていきましょう。
それぞれの半径の大きさを間違えないように気を付けてくださいね！
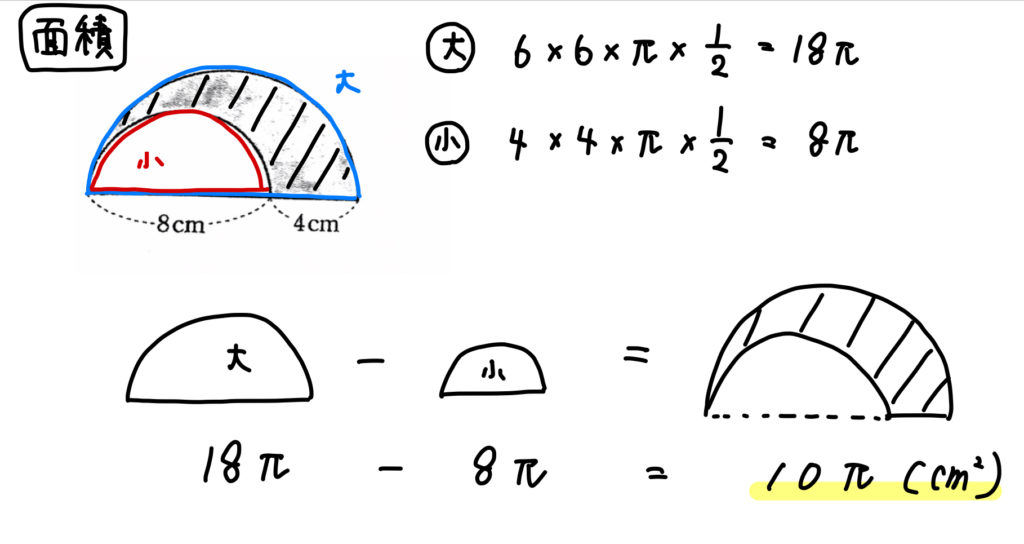
周の長さは3つのパーツ（赤、青、緑）に分けることができます。
それぞれを求めて、合計すれば周の長さとなりますね。
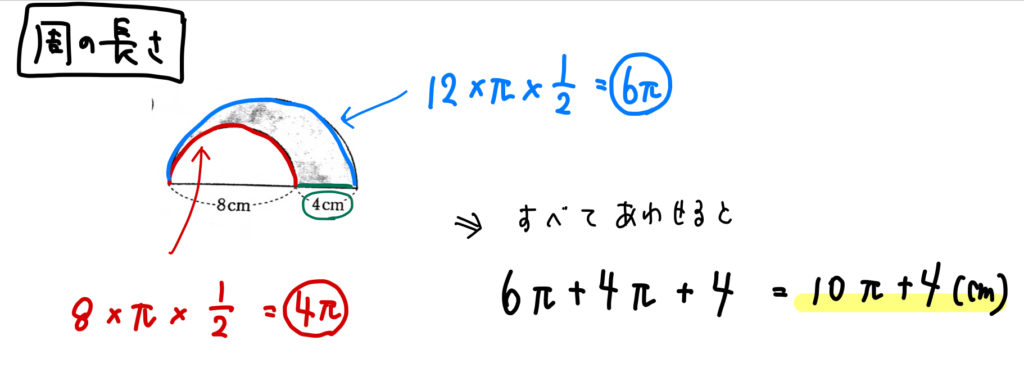
答えが式の形になってしまうので、
ちょっと違和感があるかもしれませんが、
\(10\pi\)と\(4\)はこれ以上は計算ができません。
なので、これで答えとしておいてください。
影の部分の面積、周の長さ（2）の解説
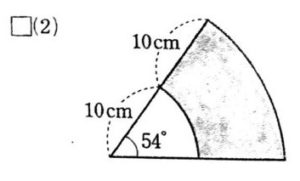
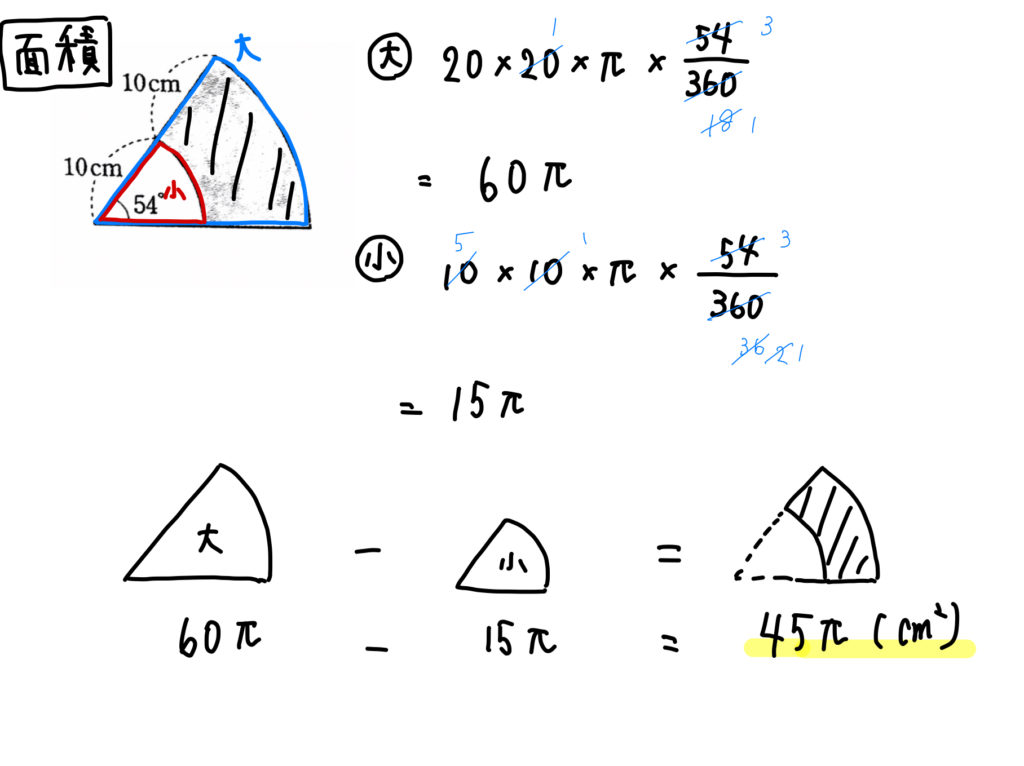
面積を求めるには、大きなおうぎ形から小さなおうぎ形を引けばよいですね。
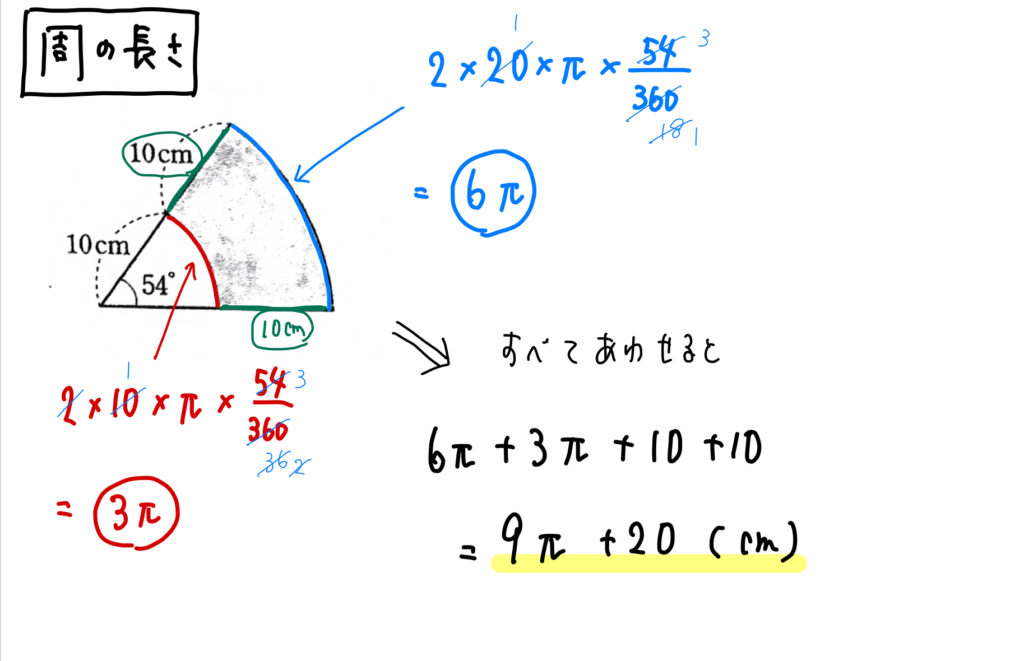
周の長さを求めるには、
小さなおうぎ形の弧（赤）、大きなおうぎ形の弧（青）
そして、それぞれの半径の差の部分（緑）に分けることができます。
それぞれを計算して、合計すると次のようになります。
影の部分の面積、周の長さ（3）の解説
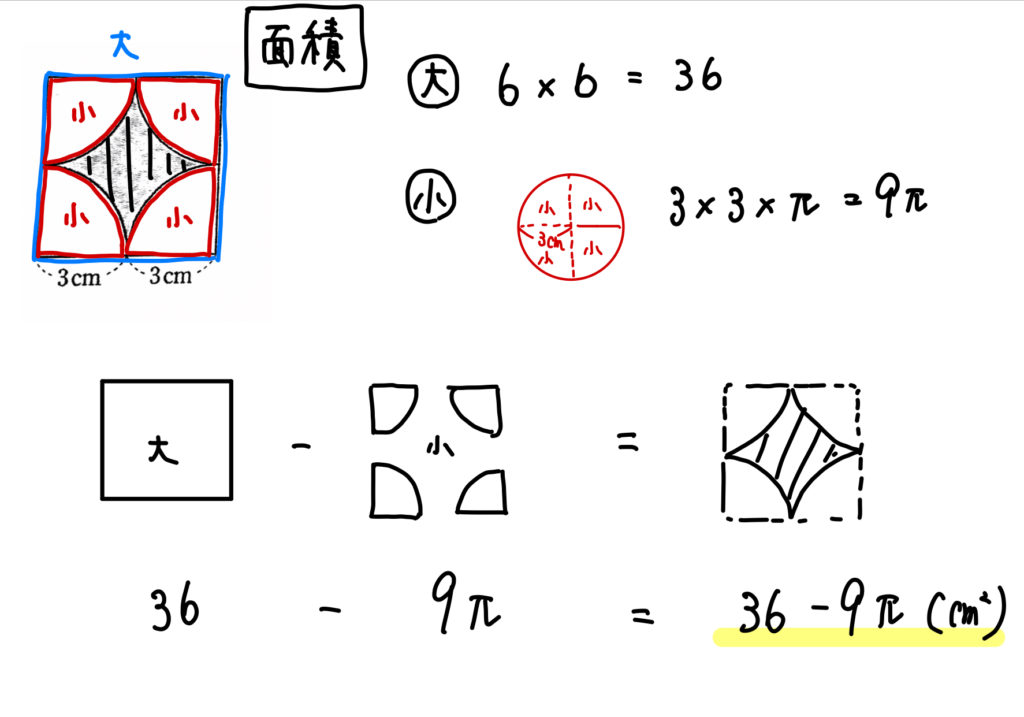
面積を求めるには、正方形からおうぎ形4つ分を引いてあげればOK。
ただ、このおうぎ形4つ分は組み合わせると1つの円になります。
このことに気が付いたら計算もラクにできますね！
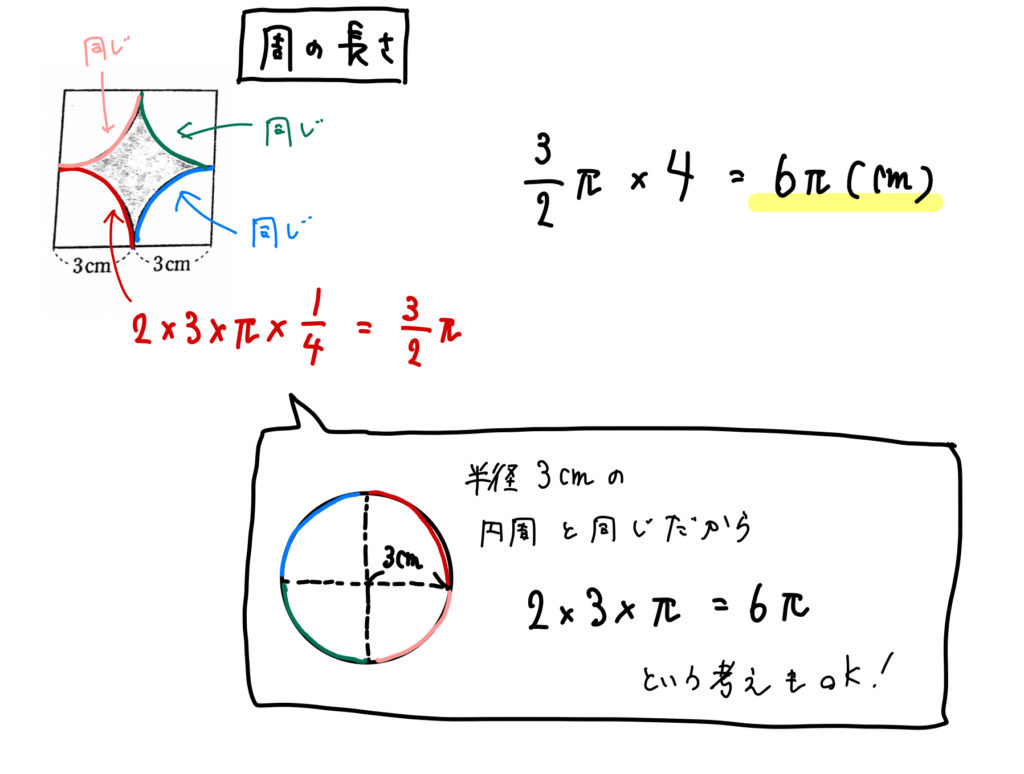
周の長さは簡単！
4つのおうぎ形の弧を合わせた長さになるのですが、
こちらも1つの円で考えてみると、計算はラクにできますね。
影の部分の面積、周の長さ（4）の解説
面積を求めるには、
おうぎ形から半円を引いてあげればOKですね。
このとき、半円の半径は6㎝になっていることにも注意です。
周の長さは、以下の3つのパーツ（赤、青、緑）を合わせれば求めることができます。
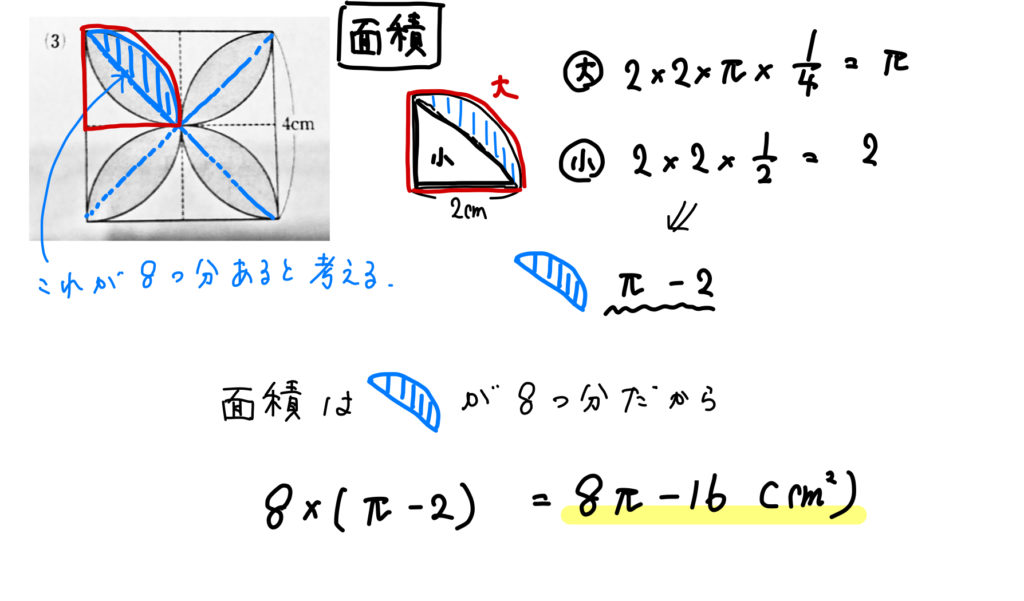
影の部分の面積、周の長さ（5）の解説
こちらはよく質問をいただく図形です。
初見では難しいかもしれませんが、
図形の見方を覚えてしまえば楽勝です。
面積を考える場合には、
次のように8等分した部分の面積を考えていきましょう。
さらに周の長さは、
次のように色分けして考えていくと簡単ですね！
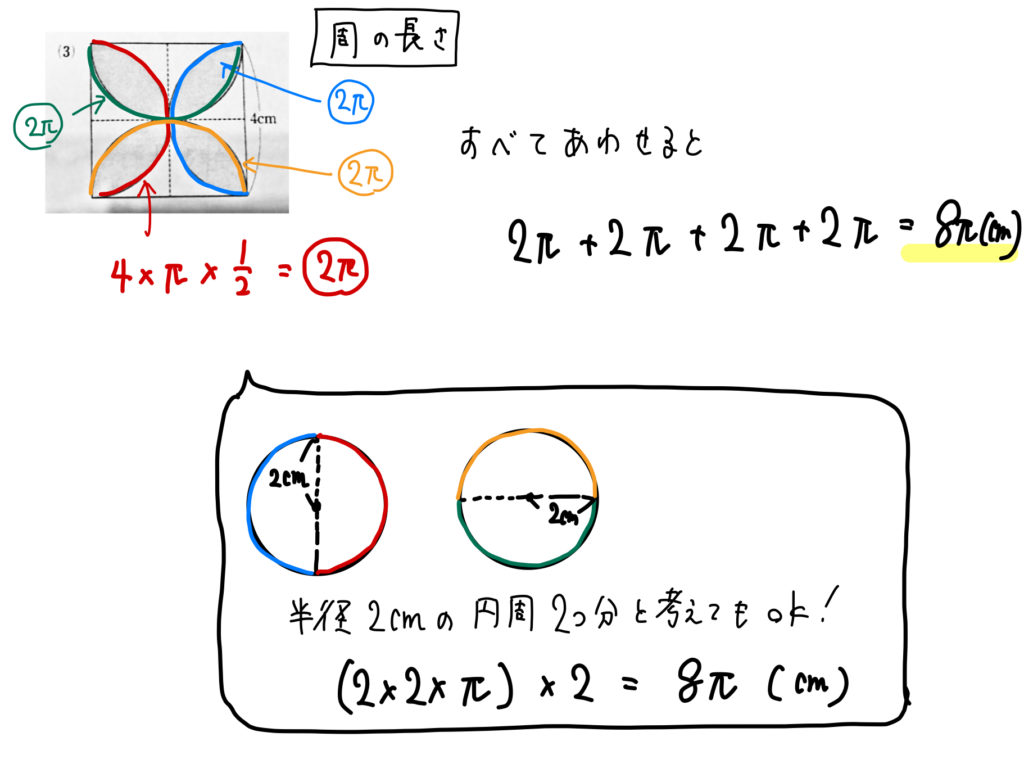
2つ分の円周の長さと等しいと考えてもOKですね。
まとめ！
お疲れ様でした！
今回はちょっと複雑なおうぎ形について扱ってみましたが、
いかがだったでしょうか？
テストで良い点を取ろうと思ったら
こういった応用問題も解けるようになっておく必要があるよね。
ちょっと難しいところもあったと思うけど、
何回も練習して必ず解けるようにしておこう！
ファイトだ(/・ω・)/
【応用】影の部分の面積、周の長さの求め方！←今回の記事
成績を上げて、志望校合格を勝ち取りたい中3生の方！
数スタの無料メルマガ講座で合格を勝ち取りませんか？
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ わからないを解決！質問対応サポート
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
コメントを残す