$$\large{x^2+y^2=(x+y)^2-2xy}$$
このように二乗足す二乗を変形する問題に出会うことがありますね。
でも、これってどのようにして変形しているか
ちゃんと理解できていますか？？
ってことで、今回の記事では二乗足す二乗の変形公式。
更には、どんな場面でこの公式を利用するのか。
また、三乗足す三乗の場合はどうなるのか？
という点について学習していきましょう。
二乗足す二乗の公式はこうやってできている！
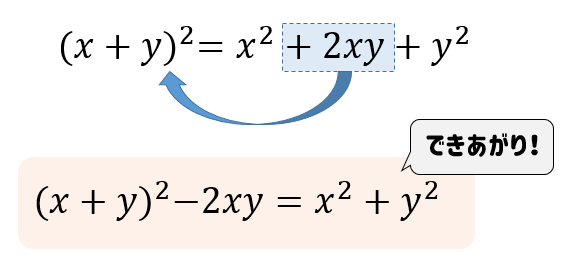
すっごく単純なことだね！
二乗の展開公式から、\(+2xy\)を移項しただけ。
ってことは、同様に考えると
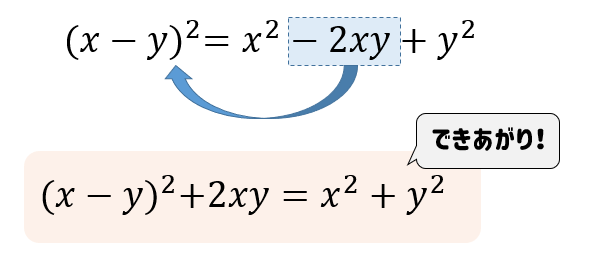
このように符号を変えた変形も可能だということが分かるね！
二乗足す二乗の公式
$$x^2+y^2=(x+y)^2-2xy$$
$$x^2+y^2=(x-y)^2+2xy$$
二乗足す二乗の公式を使う問題
\(x=\frac{2+\sqrt{3}}{2-\sqrt{3}}\), \(y=\frac{2-\sqrt{3}}{2+\sqrt{3}}\) のとき、次の式の値を求めなさい。
$$x^2+y^2$$
こういう問題がまさに、二乗足す二乗の公式が役立つ場面です。
そのまま、\(x,y\)に代入すると…すごくメンドイよねｗ
なので、\(x^2+y^2=(x+y)^2-2xy\) と変形をしてから代入する。
すると、計算がラクにてきるよう問題が設計されていることが多いです。
では、実際に計算してみましょう。
そのまま代入すると式が長くなってしまうので、\(x+y\),\(xy\) を別々に計算していきますね。
$$\begin{eqnarray}x+y&=&\frac{2+\sqrt{3}}{2-\sqrt{3}}+ \frac{2-\sqrt{3}}{2+\sqrt{3}}\\[5pt]&=&\frac{(2+\sqrt{3})^2}{4-3}+\frac{(2-\sqrt{3})^2}{4-3}\\[5pt]&=&(4+4\sqrt{3}+3)+(4-4\sqrt{3}+3)\\[5pt]&=&14\end{eqnarray}$$
$$\begin{eqnarray}xy&=&\frac{2+\sqrt{3}}{2-\sqrt{3}}\times \frac{2-\sqrt{3}}{2+\sqrt{3}}\\[5pt]&=&1 \end{eqnarray}$$
よって
$$x^2+y^2=(x+y)^2-2xy=14^2-2\times 1=194$$
答え
$$194$$
そのまま代入して計算するよりも、かなりラクにできたね(^^)
このように、\(x^2+y^2\) の式の値を求めるような問題では二乗足す二乗の公式を使って式変形をしていきましょう。
どうやって変形すればいいか忘れた…
という方は、二乗の展開公式を思い出してください。
\(2xy\) の部分を移項するだけで、簡単に導くことができますよ(/・ω・)/
三乗足す三乗の場合は？
二乗足す二乗の公式は、展開公式から導けることが理解できると
三乗足す三乗が出てきてもバッチリです！
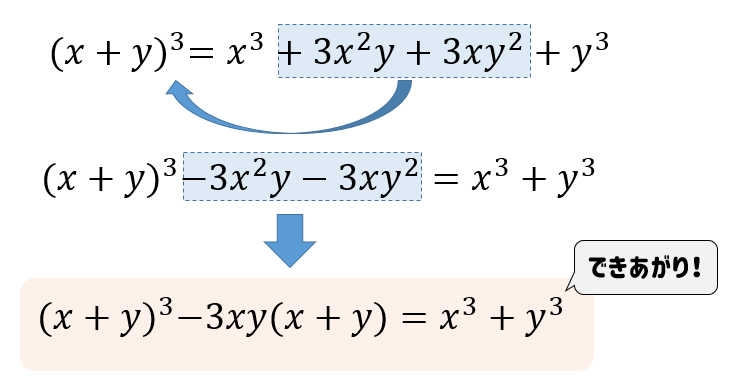
こちらも合わせて覚えておくといいですね(^^)
ただし、三乗足す三乗の場合
$$(x+y)(x^2-xy+y^2)=x^3+y^3$$
という展開公式があったのを覚えていますでしょうか？
これも活用することができるので、三乗足す三乗を変形する式はちょっとバリエーションが多めとなっています。
三乗足す三乗の公式
$$x^3+y^3=(x+y)^3-3xy(x+y)$$
$$x^3+y^3=(x+y)(x^2-xy+y^2)$$
まとめ！
二乗足す二乗の公式は簡単だ！
しっかりと展開公式を覚えておけば、自分で導くことができます。
あれ、どうだっけ…となってもすぐに思い出せるので楽勝ですね(^^)
二乗足す二乗の公式
$$x^2+y^2=(x+y)^2-2xy$$
$$x^2+y^2=(x-y)^2+2xy$$
中学生向けの英文法サイトを開設！
≫ 中学英語の文法まとめサイト！