不等式の解き方まとめ！高校数学はこれでバッチリ！

今回は高校数学Ⅰで学習する

「不等式の解き方」

について徹底解説していくよ！

不等式と言っても

連立不等式、絶対値の不等式、文字を含む不等式、二次不等式…

このようにバリエーションは様々

今回の記事では、それらの問題をぜーんぶ解説していくよ！

不等式の解法まとめ記事にしていくんで、ぜひ参考にしていってください(^^)

一次不等式の解き方

一次不等式は方程式の解き方を理解している方にとっては楽勝！

気を付けておきたいポイントは１つだけです。

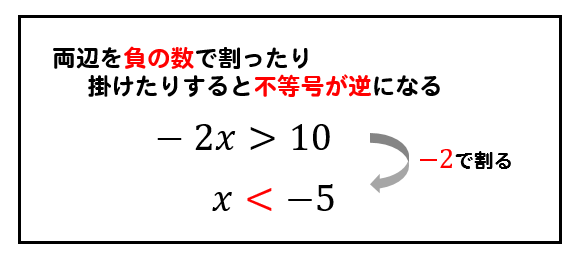
このように、負の数で掛けたり割ったりするときには不等号の向きが逆になります。

この点だけ気を付けておけば大丈夫！

それでは、例題を見ていきましょう。

方程式の解き方が不安な方はこちらの記事で復習しておいてね(^^)

＞一次方程式の解き方をまとめておくよ！基本計算～分数、小数まで

一次不等式の解き方について、こちらの動画でもサクッと解説しています(‘◇’)ゞ

（1）の基本解法

$$6x-20>2x$$

$$6x-2x>20$$

$$4x>20$$

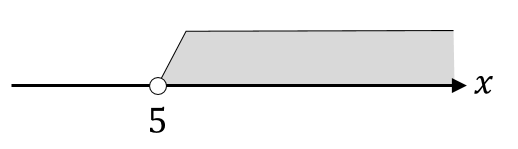
$$x>5$$

数直線で範囲を表すとこんな感じになります。

（2）の基本解法

まずは、かっこを外して不等式を解いていきましょう。

$$4(x-2) ≦ 5(2x-3)$$

$$4x-8 ≦ 10x-15$$

$$4x-10x ≦ -15+8$$

$$-6x ≦ -7$$

両辺を\(-6\)で割るので不等号の向きは逆になります。

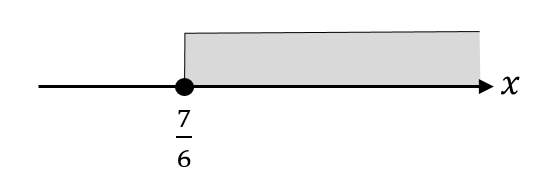
$$x ≧ \frac{7}{6}$$

数直線で範囲を表すとこんな感じ！

一次不等式（分数の場合）

分数の場合には、分母の最小公倍数を両辺にかけてシンプルな不等式になるよう変形していきましょう。

（1）の分数解法

分母にある３、２、４の最小公倍数である１２を両辺にかけます。

$$\displaystyle{\frac{2}{3}x\times 12-\frac{1}{2}\times 12≧12\times \frac{3}{4}(x-1)}$$

$$8x-6≧9(x-1)$$

$$8x-6≧9x-9$$

$$-x≧-3$$

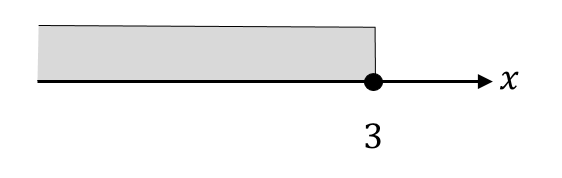
$$x≦3$$

（2）の分数解法

分母の数である５と３の最小公倍数１５を両辺にかけます。

$$\frac{3x+2}{5}\times 15<\frac{2x-1}{3}\times 15$$

$$(3x+2)\times 3<(2x-1)\times 5$$

$$9x+6<10x-5$$

$$9x-10x<-5-6$$

$$-x<-11$$

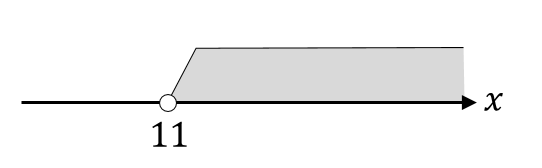
$$x>11$$

一次不等式（小数の場合）

小数の場合には、両辺を10倍、100倍することで小数を消してやりましょう！

（1）の小数解法

小数を消すために両辺を10倍してやりましょう。

$$(0.4x-0.7)>(1.3x+2)\times 10$$

$$4x-7>13x+20$$

$$4x-13x>20+7$$

$$-9x>27$$

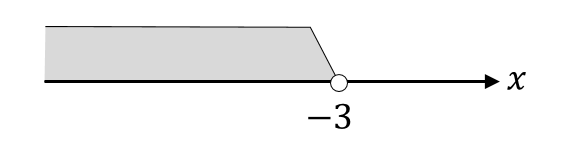
$$x<-3$$

小数を消すためには、すべての項を10倍してやってくださいね！

（2）の小数解法

両辺を10倍して小数を消してやりましょう。

$$(0.2x+1)\times 10≦(-0.3x-2.5)\times 10$$

$$2x+10≦-3x-25$$

$$2x+3x≦-25-10$$

$$5x≦-35$$

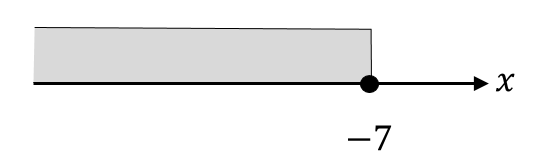
$$x≦-7$$

連立不等式の解き方

連立不等式を解く場合には、連立方程式のように加減法や代入法を使いません。

連立不等式の解き方手順は以下の通りです。

それでは例題を見てみましょう！

連立不等式については、こちらの動画でもサクッと解説しています(‘◇’)ゞ

（1）の連立不等式解法

まずは、それぞれの不等式を解いてやります。

$$5x+1≦8x+16$$

$$5x-8x≦16-1$$

$$-3x≦15$$

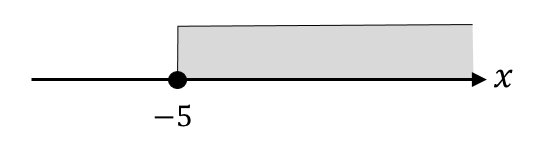
$$x≧-5$$

$$2x -3 < -x+6$$

$$2x+x<6+3$$

$$3x<9$$

$$x<3$$

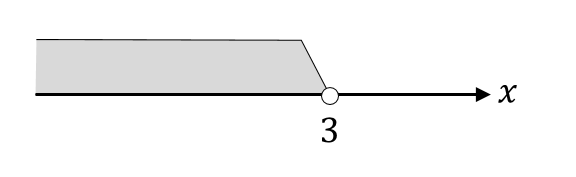
それぞれの不等式が解けたら、同じ数直線上に範囲を書いて共通している部分を見つけましょう。

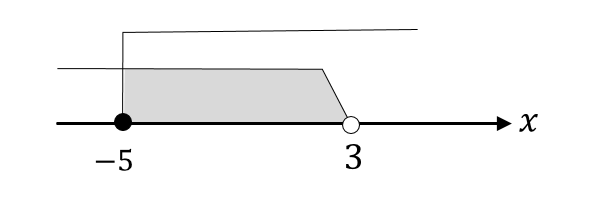
すると、このように\(-5\)から\(3\)までの範囲が共通している部分だと読み取れます。

よって、答えは

$$-5≦x<3$$

となります。

それぞれの不等式を解く！

共通範囲を読みとる！

以上！

簡単だね(^^)

（2）の連立不等式解法

まずは、それぞれの不等式を解きましょう。

$$6x-5<2x+7$$

$$6x-2x<7+5$$

$$4x<12$$

$$x<3$$

$$x +8 ≧ 5x$$

$$x-5x≧-8$$

$$-4x≧-8$$

$$x≦2$$

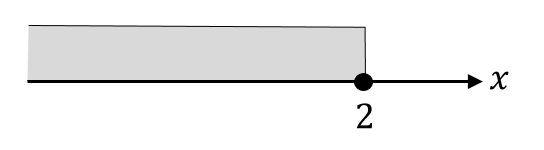
それぞれの解から共通範囲を求めると

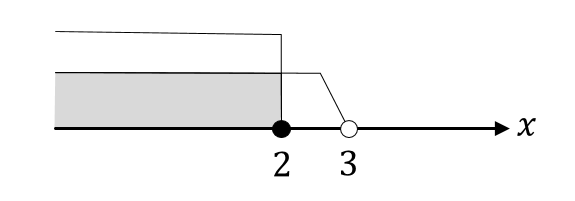
答えは

$$x≦2$$

だということが読み取れます。

３つの不等式の解き方

不等式が３つもある場合には、2つに分ける！

というのがポイントとなります。

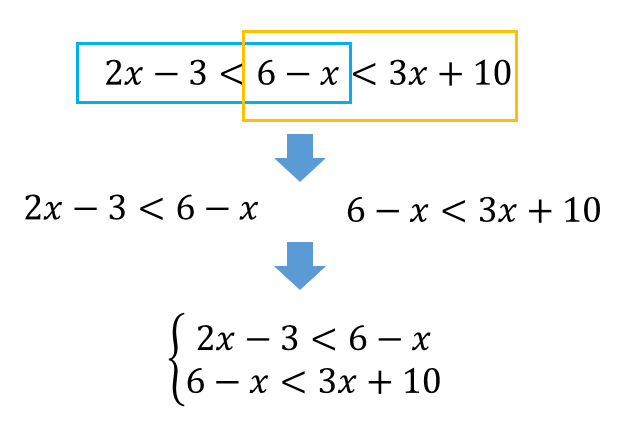
このように、３つあった不等式を２つに分けて連立不等式を作ってやります。

連立不等式が作れたら、あとは計算あるのみです(^^)

それぞれの不等式を解いて共通範囲を求めていきましょう。

$$2x-3<6-x$$

$$2x+x<6+3$$

$$3x<9$$

$$x<3$$

$$6-x<3x+10$$

$$-x-3x<10-6$$

$$-4x<4$$

$$x>-1$$

それぞれの解の共通範囲は

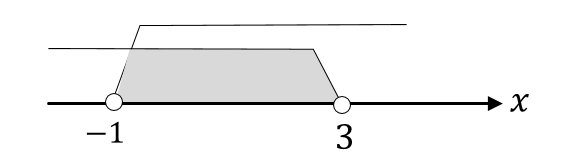
このようになります。

よって、答えは

$$-1<x<3$$

となります。

不等式が３つ出てきた場合には、２つに分けて連立！

絶対値の不等式の解き方

次は絶対値を含む不等式の解き方について解説していきます。

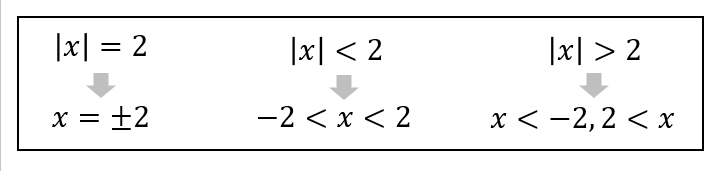
絶対値を含む方程式、不等式では上のような式変形ができることをおさえておきましょう。

それでは例題を見ていきます。

（1）の絶対値解法

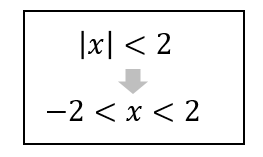
この形の変形を利用して解いていきましょう。

$$|x+7|<2$$

$$-2<x+7<2$$

$$-2-7<x+7-7<2-7$$

$$-9<x<-5$$

（2）の絶対値解法

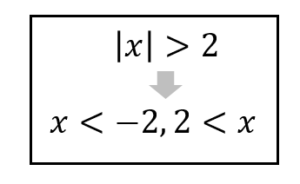
この形の変形を利用して解いていきましょう。

$$|2x-1|≧3$$

$$2x-1≦-3,   3≦2x-1$$

$$2x≦-3+1,   3+1≦2x$$

$$2x≦-2,   4≦2x$$

$$x≦-1,   2≦x$$

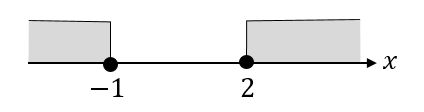
絶対値の不等式（場合分けが必要）の解き方

次の不等式を解きなさい。

$$|x-4|<3x$$

この不等式は、絶対値の外に\(x\)がはみ出しちゃってるよね

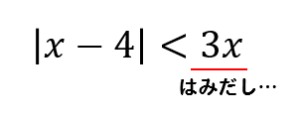
こういうときには、上で解いたようなやり方ではなく絶対値の場合分けが必要となってきます。

絶対値の中身が０以上か、負になるか

この2パターンで分けていきます。

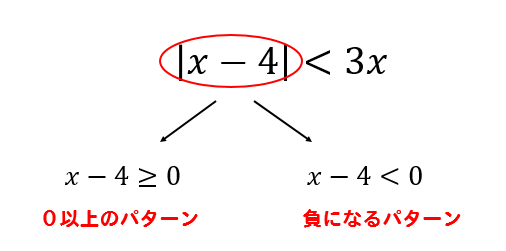
それではそれぞれのパターンにおいて不等式を解いていきます。

まずは絶対値の中身が0以上になるパターンから

\(x-4≧0\)つまり\(x≧4\)のとき

絶対値の中身は0以上なので、そのままの形で絶対値を外すことができます。

よって

$$x-4<3x$$

という不等式ができあがります。

あとは、この不等式を解いていきましょう。

$$x-3x<4$$

$$-2x<4$$

$$x>-2$$

このように解を求めることができました。

しかし、この不等式を解く上での前提条件として\(x≧4\)となっています。

だから、求めたい答えはそれぞれの共通範囲を取ってやって

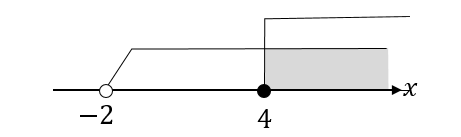
答えは

$$4≦x$$

となります。

場合分けをしたときの前提条件となる範囲を出しているはずなので、それを忘れないようにしましょう。

次は、絶対値の中身が負になるパターンを考えます。

\(x-4<0\)つまり\(x<4\)のとき

絶対値の中身が負になる場合には、マイナスをつけて絶対値をはずすことができます。

よって

$$-(x-4)<3x$$

という不等式ができあがります。

あとは、この不等式を解いていきましょう。

$$-x+4<3x$$

$$-x-3x<-4$$

$$-4x<-4$$

$$x>1$$

場合分けの前提条件である\(x<4\)と合わせてやると

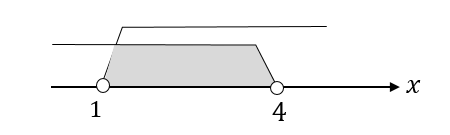
答えは

$$1<x<4$$

となります。

以上より、この不等式には

\(4≦x\)と\(1<x<4\)

２つの解があることが分かりました。

これで答えが求まった！ということになるのですが

この２つの範囲をよく見てみると…

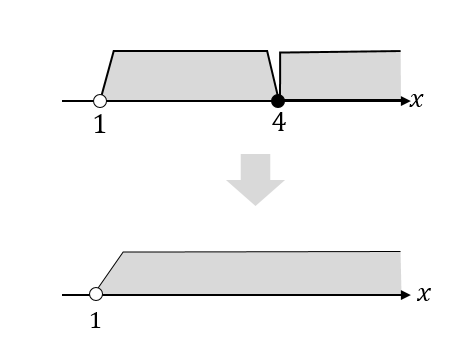
あ、つながってんじゃん！

ということに気が付くはずです。

なので、答えを書くときには

\(4≦x\)と\(1<x<4\)というように別々に書くのではなく

$$1<x$$

というようにまとめて書いてやりましょう。

絶対値の外に\(x\)がはみ出してしまっているときには場合分けを使いましょう。

絶対値の中身が0以上、負になるパターンで分けます。

そして、それぞれの前提条件に気をつけながら不等式を解きます。

それぞれの不等式が求まったら、範囲が繋がるかどうかを確かめます。

繋がってしまう場合には、まとめた形で答えを書きましょう。

応用（満たす整数を考える問題）

次は不等式の応用問題を考えてみましょう。

模試や入試によく出題される問題なので、しっかりと理解しておこう。

（1）満たす自然数の値を求める

自然数とは正の整数

つまり、１，２，３，４，５…といった数のことだったね。

そのことを頭に入れておいて問題を考えていこう。

まずは不等式を解いていきます。

$$5x-7<2x+5$$

$$5x-2x<5+7$$

$$3x<12$$

$$x<4$$

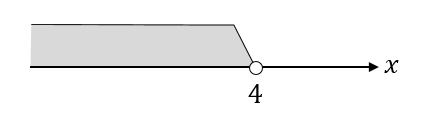
次に、この範囲の中に入っている自然数を見つけていきましょう。

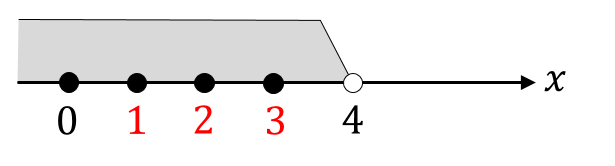
すると、１，２，３という数字が見つかります。

範囲が4未満となっているので、４は含めないようにしてくださいね。

更に０は自然数に含まれないことも注意です。

よって、答えは１，２，３となります。

（2）定数\(a\)の値の範囲を求める

まずは、連立不等式を作って解を求めてみましょう。

\(\begin{eqnarray} \left\{ \begin{array}{l} 8 -2x < 2x \\ 2x  < x+a \end{array} \right. \end{eqnarray}\)[/aside]

それぞれの不等式を解くと

$$8-2x<2x$$

$$-2x-2x<-8$$

$$-4x<-8$$

$$x>2$$

$$2x<x+a$$

$$2x-x<a$$

$$x<a$$

\(a\)の値が不明なので、共通範囲を求めようにも正確な範囲が分かりません…

しかし、問題文より共通範囲の中に整数がちょうど4個存在するということが与えられています。

そのことから\(a\)の値は…

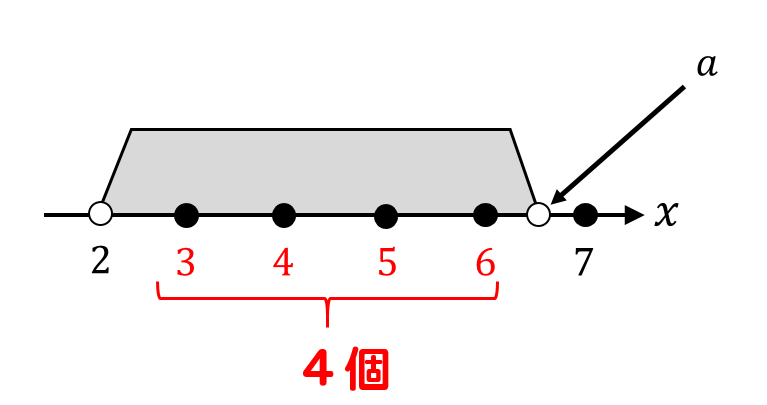
このように、６と７の間にあれば良いということが分かります。

次に、\(a\)の値について詳しくチェックしていきます。

６と７の間ということは分かったけれど

\(a\)が６になったとき、７になったときに条件を満たすかどうかを調べていきます。

\(a=6\)のとき

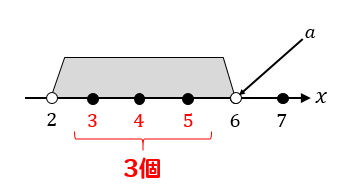
共通範囲に入っている整数は3個になってしまいます。

これでは問題文の条件を満たさなくなるので、\(a=6\)はダメということが分かります。

次に\(a=7\)のとき

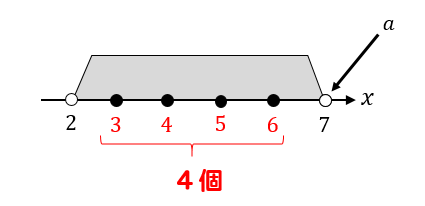
共通範囲に入っている整数は4個となります。

これは問題文で与えられた条件を満たしているので、\(a=7\)はOKだということが分かります。

以上のことから

\(a\)の値は6から7の間に入っていて

6はダメで7はOKということになります。

これを数式で表すと

$$6<a≦7$$

このように答えを求めることができました。

今回のように\(a\)の値の範囲を求める問題では、まず\(a\)の値がどこら辺にあるのかという場所をつきとめます。

次にその範囲の端である数はOKなのかどうかを調べます。

最後にそれらの情報をまとめて数式で表してやれば完成です(^^)

二次不等式の解き方

二次不等式の解き方については、ボリュームが多くなりそうなので別記事にて解説していくよ(^^)

＞二次不等式の解き方を簡単に！高校数学をマスターしよう！

まとめ

お疲れ様でした！

以上で不等式の解説はおわりっ★

不等式で困ったことがあれば、この記事を参考にしてもらえると嬉しいです(^^)

まだ解説が必要だという問題があれば随時追記していきますね！

みんなファイトだ(/・ω・)/