【中１方程式】一次方程式の解き方をまとめておくよ！基本計算～分数、小数まで

こんにちは！数スタの小田です。

今回の記事では、中１で学習する一次方程式の解き方についてまとめていくよ！

 

基本的な方程式の解き方から分数、小数を含む方程式の解き方まで説明していきます。

分数、小数が出てくると難しく思えちゃうんだけど、ある手順をしっかりと踏めば簡単に解けるようになるからね！

なるべく丁寧に説明するつもりだから、この記事を通して方程式の理解を深めてもらえればと思います＾＾

 

さぁ、いきましょー！

 

こちらの動画でも方程式の解き方について解説しています(/・ω・)/

 

方程式の基本的な解き方

方程式の解法手順をまとめておくと以下のようになります。

 

それでは、例題を通して方程式の解き方を確認してみましょう。

 

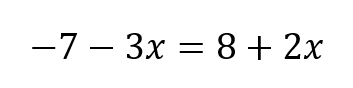
それでは手順通り見ていきましょう。

① 文字の項を左辺、数の項を右辺に移項する。

まずは、文字の項を左辺、数の項を右辺に移項します。

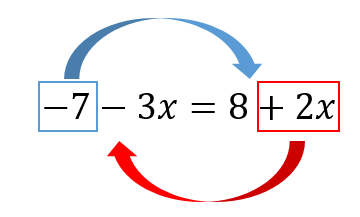
ちなみに移項というのは、項をイコールの反対側へ符号を変えて移動させることだよ。

それぞれを移項させるとこのような式になります。

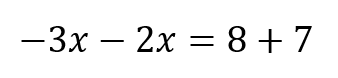
右辺にあった\(2x\)は符号が変わって左側へ

左辺にあった\(-7\)も符号が変わって右側へ動いています。

② 両辺をそれぞれ計算してまとめる。

それぞれ移項ができたら、左辺右辺をまとめていきます。

 

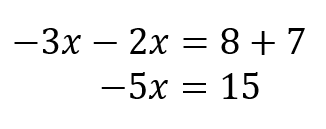
③ \(x\)の前についている数が負の数の場合、両辺に\(\times (-1)\)をして符号を変える。

左辺、右辺をまとめた式を見てみると、\(x\)の前にある数が負の数になっています。

この場合には両辺に×(－1)をすることによって、今後の計算を少し楽にしてやることができます。

 

④ \(x\)の前についている数で両辺をわる。

最後は\(x\)の前についている数で両辺を割ります。

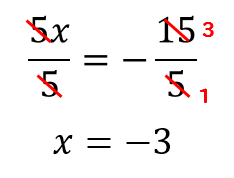
以上！

これで方程式の解は\( x=-3 \)だということが求めれました。

 

 

最後に式変形を通してみておきましょう。

 

 

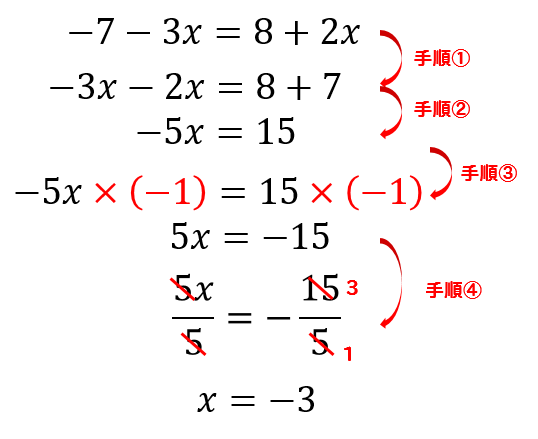
一次方程式は基本的にこの手順で全て解くことができます。

しかし、中には手順１に入る前の前段階ともいえる【手順０】を必要とする方程式もあります。

次では、そのような手順０を必要とする方程式を見ていきましょう。

【手順０】が必要な小数、分数の方程式

基本的には上で紹介した手順１～４で解けるのですが

小数や分数を含む方程式に関しては、手順１の前段階に当たる【手順０】ともいうべき一工夫が必要になります。

手順０とはどんなものか。

一緒に確認していきましょう。

 

小数を含む方程式の【手順０】

 

 

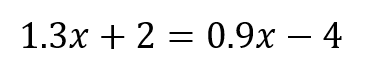
方程式に小数が含まれている場合には、まず両辺を10倍、100倍して小数を消します。

今回の場合、方程式に含まれている小数は全て小数以下の位が１つだけなので両辺を10倍します。

1.31のように小数点以下の位が2つある小数が含まれていれば100倍

1.312のような小数が含まれていれば1000倍というように

両辺にかける数を選択してください。

 

では、両辺を10倍すると

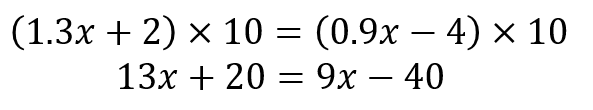
このように小数が消えてしまいます。

これが手順０ですね。

 

これ以降は上で紹介した手順通りに変形して

 

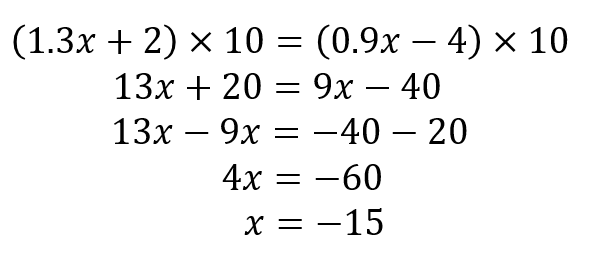
分数を含む方程式の【手順０】

 

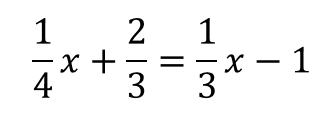
方程式に分数が含まれている場合、分母の最小公倍数（通分する数）を両辺にかけて分数を消してやります。

今回は分母の数が3と4なので最小公倍数である12を両辺にかけます。

 

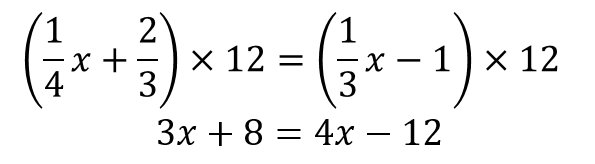
そうすると両辺から分数が消えました。

これが分数が含まれている方程式の手順０ですね。

 

以下は手順１～４で変形していきます。

 

 

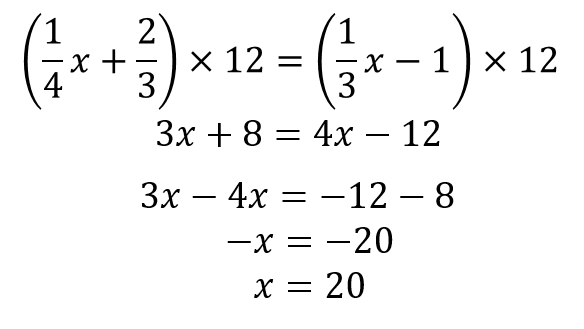
このように小数、分数を含む方程式に関しては【手順０】を加えることで簡単に解くことができるようになります。

【特典】方程式のミスりポイントをまとめてみました！

さて、ここまでのところで方程式の解き方は理解してもらえたと思います＾＾

ですが、いざ問題にチャレンジしてみると意外な落とし穴が待っているんですね…汗

 

というのも、方程式の基本をバッチリに仕上げた学生さんに問題を解かせてみると、「答えが分数になるやつ」「かっこで符号が変わるやつ」「分数のかけ忘れ」「小数の見落とし」などなど、みんなが揃って間違えてしまう共通のポイントがあったのです…！

 

こういった問題への対処をしっかりと対策しておかないと、テストでミスを連発して点数が落ちてしまいます(._.)

というわけで、僕が中1の学生さんに方程式を指導するときにはこういった見落としポイントを克服するための演習プリントを活用しています。これらを一通りやることで事前にミスりやすいポイントとその解決方法を学べるのでしっかりとテストで満点を取ることができています＾＾

 

そこで、今回の記事を通して方程式の基本的な流れを身につけてもらえた方には、次のステップとして僕が指導するときに活用しているプリントをお渡しするので、見落としポイントを克服してテストで満点をゲットしてもらいたいです(‘ω’)ノ

 

この課題を活用してみたい！という方にはメールでプリントを送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので、ぜひご活用ください＾＾

 

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

方程式の解き方まとめ

方程式の基本的な解法手順は以下の通りです。

1. 文字の項を左辺、数の項を右辺に移項する。
2. 両辺をそれぞれ計算してまとめる。
3. xの前についている数が負の数の場合、両辺に×(－１)をして符号を変える。
4. xの前についている数で両辺をわる。

 

ただし、方程式に小数、分数を含む場合には【手順０】を加えましょう。

 

方程式の解法については説明した通り

手順１～４を踏んでいけば、どんな方程式でも解くことができるはずです。

そして、分数や小数が含まれている場合でも【手順０】をやってやれば大丈夫ですね！

あとは実戦練習を通して、計算の力を高めていきましょう。

 

ファイトだ！

 

方程式の解き方を理解できたら、次は文章問題に挑戦してみましょう。

>代金の文章問題を解く方法について解説！

>何分後に追いつくか？速さの問題を解説！

>余る？足りない？過不足の問題を解説！

>年齢の求め方は？文章問題を解説！