高さがわからない二等辺三角形の面積の求め方！三平方の定理を使えばバッチリ！

二等辺三角形の面積を求めなさい。

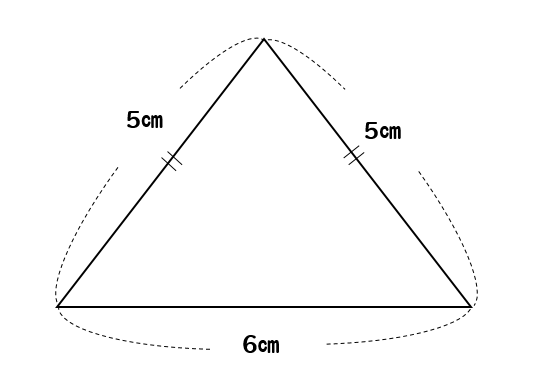
あれ…

高さがわからないけど、どうすんの！？

受験レベルの問題に挑戦していくと

このような応用問題に出会うことがあります。

このよう場合には

中3の終盤で学習する『三平方の定理』を用いて

高さを求めていくようになります。

今回は、三平方の定理を用いて

二等辺三角形の高さを求める方法について

徹底解説していきます！

二等辺三角形の高さを求める方法

上でも言ったように

二等辺三角形の高さを求めるためには

三平方の定理というものを利用していきます。

というわけで、少しだけ三平方の定理について確認しておきましょう。

三平方の定理の基本公式

直角三角形において

斜辺の長さを2乗すると、他の辺の長さの2乗の和に等しくなる。

というのが三平方の定理でした。

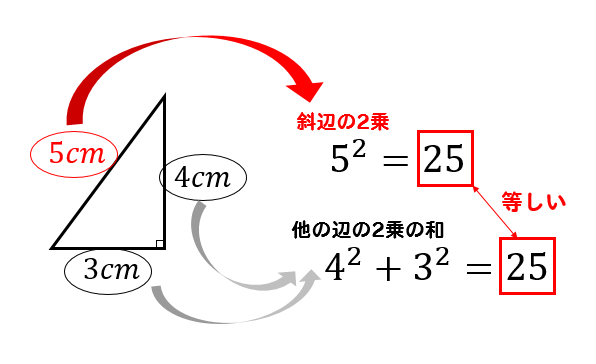
具体的には、こういうことでしたね。

そして、直角三角形の中でも

特別な存在のやつらがいました。

45°、45°、90°という角を持つ直角二等辺三角形は

辺の長さの比が\(1:1:\sqrt{2}\)となる。

30°、60°、90°という角を持つ直角三角形は

辺の長さの比が\(1:2:\sqrt{3}\)となる。

というような特徴がありました。

詳しくはこちらの記事で解説しているので参考にしてね。

【三平方の定理】覚えておきたい基本公式を解説！

これらのことを踏まえた上で

二等辺三角形の高さの求め方について解説を進めていきます。

二等辺三角形を2分割して高さを求める！

二等辺三角形の高さを求めるためには

頂角から垂直に線を引いて

二等辺三角形を2分割してやります。

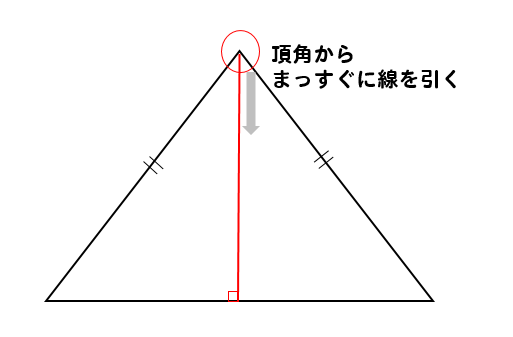
すると、二等辺三角形の特徴から

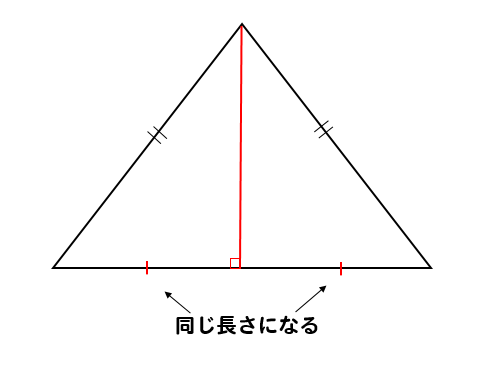
底辺の長さが二等分されるんですね。

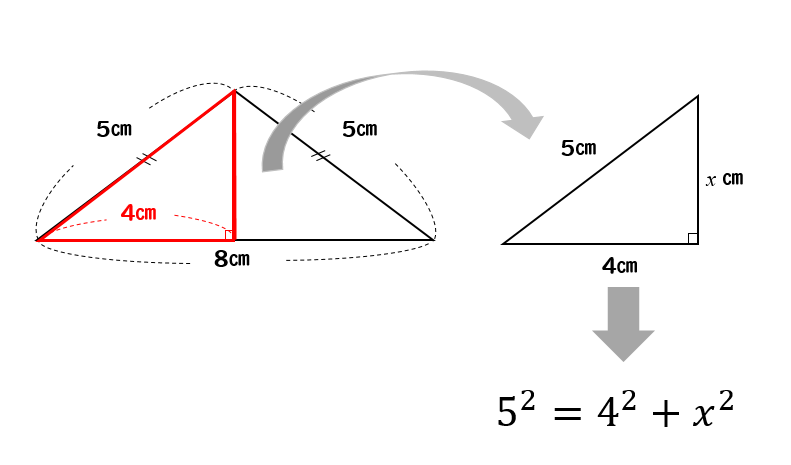
今回の問題で考えると

こういうことになります。

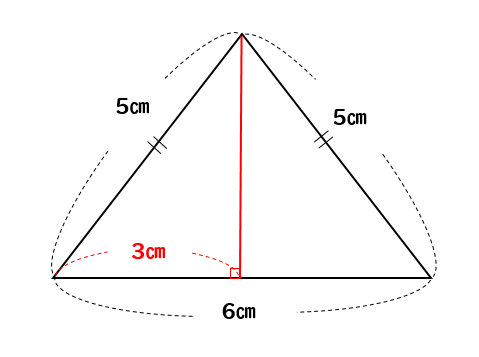
次に、直角三角形に注目して

三平方の定理を使って高さを求めていきましょう。

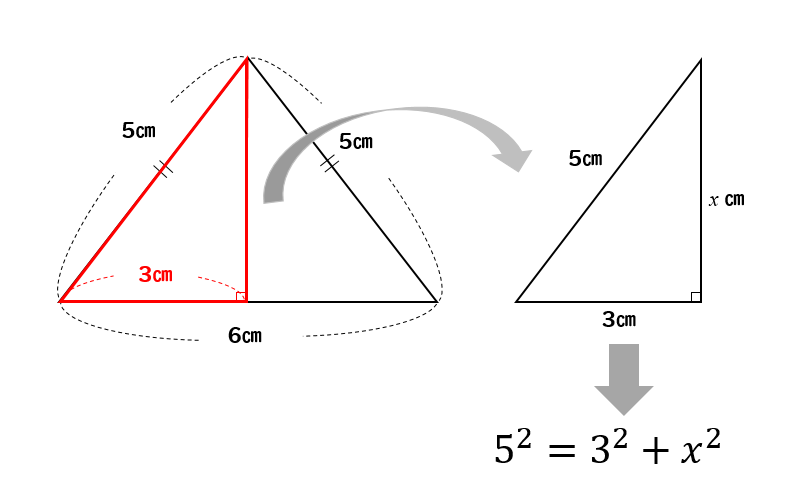
$$5^2=3^2+x^2$$

$$25=9+x^2$$

$$x^2=16$$

$$x=\pm 4$$

\(x>0\)だから

$$x=4$$

このようにして二等辺三角形の高さを求めることができます。

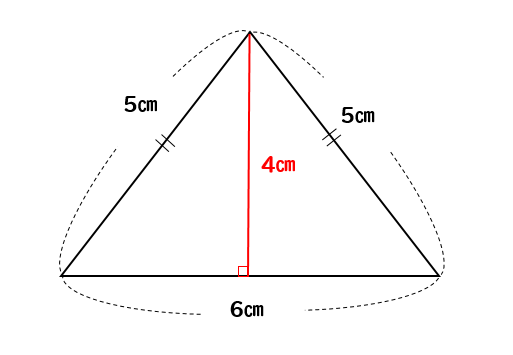
高さを求めることができれば

$$(三角形の面積)＝(底辺)\times(高さ)\times\frac{1}{2}$$

なので

$$3\times4\times \frac{1}{2}=6 cm^2$$

このように面積を求めることができました。

それでは、いくつか練習問題を通して

理解を深めておきましょう。

演習問題で理解を深める！

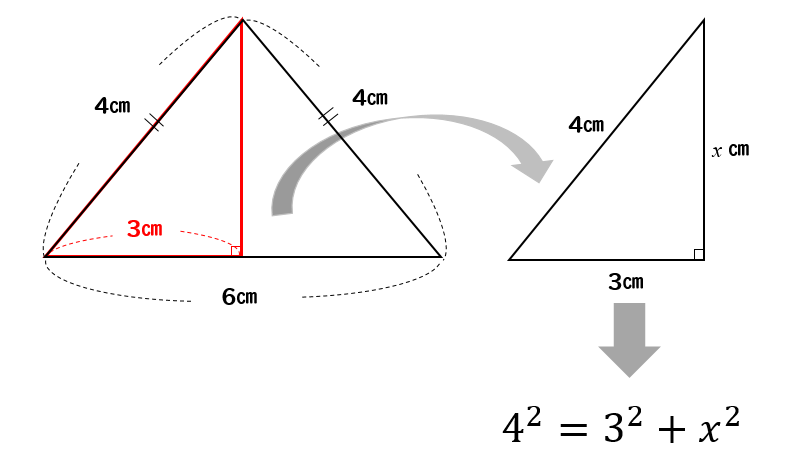
次の二等辺三角形の面積を求めなさい。

(1)答えはこちら

（1）答え

$$12 cm^2$$

頂角からまっすぐな線を引いて高さを求めていきましょう。

$$5^2=4^2+x^2$$

$$25=16+x^2$$

$$x^2=9$$

$$x=\pm 3$$

\(x>0\)だから

$$x=3$$

 

よって、面積は

$$8\times3\times\frac{1}{2}=12 cm^2$$

(2)答えはこちら

（2）答え

$$3\sqrt{7} cm^2$$

頂角からまっすぐな線を引いて高さを求めていきましょう。

$$4^2=3^2+x^2$$

$$16=9+x^2$$

$$x^2=7$$

$$x=\pm \sqrt{7}$$

\(x>0\)だから

$$x=\sqrt{7}$$

 

よって、面積は

$$6\times\sqrt{7}\times\frac{1}{2}=3\sqrt{7} cm^2$$

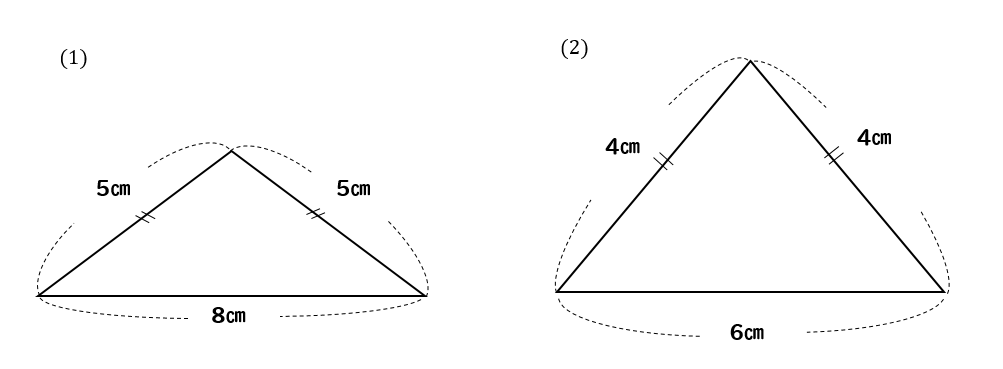
直角二等辺三角形の場合は？

直角二等辺三角形の場合

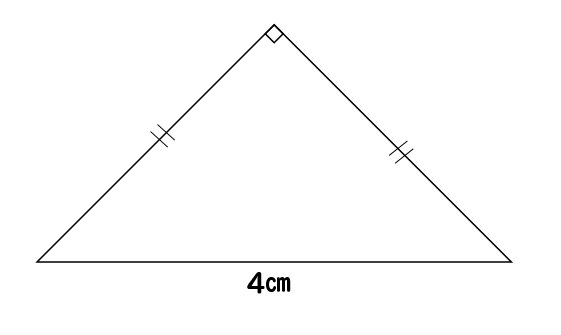
このように1辺しか長さを教えてもらえませんが

高さを求めることができます。

直角二等辺三角形って

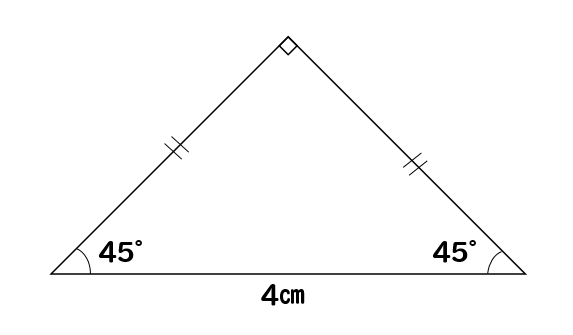
このように角度がわかります。

これは特別な直角三角形だから

比が使えるやつだね！

そして

先ほどと同じように頂角からまっすぐな線を引いて考えていくと

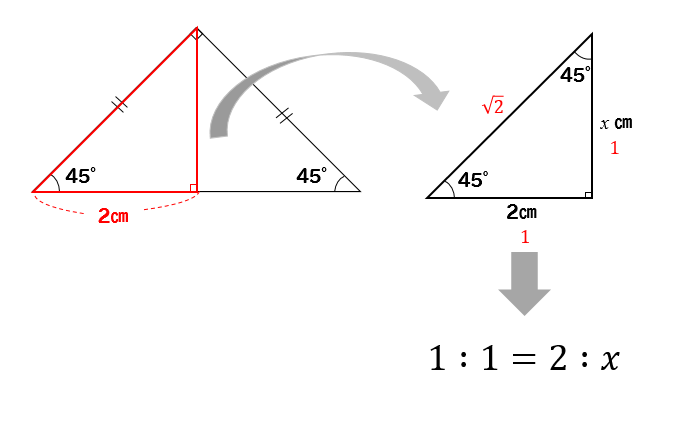
$$1:1=2:x$$

$$x=2$$

このように比を使っていくことで

高さを求めることができます。

面積は

$$4\times\ 2 \times \frac{1}{2}=4 cm^2$$

となります。

正三角形の場合は？

正三角形の場合はどうでしょうか？

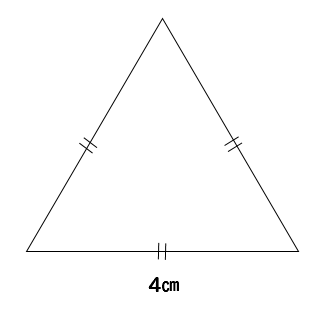
この場合も長さが1辺しかわからなくてもOKです。

正三角形の角度は

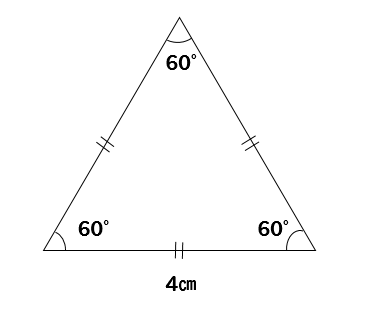
このように全て60°になっているので

頂角からまっすぐな線を引いて

直角三角形を作ってやると

30°、60°、90°の特別な直角三角形になります。

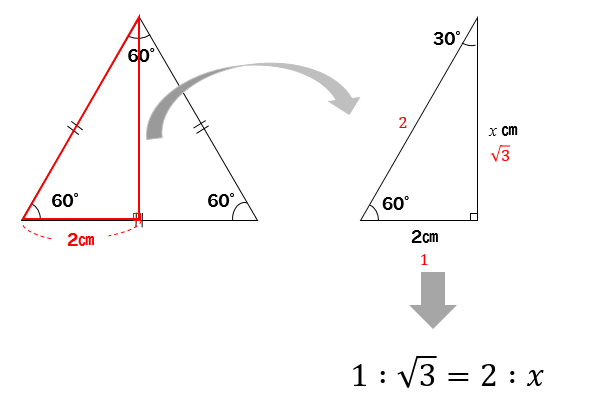
$$1:\sqrt{3}=2:x$$

$$x=2\sqrt{3}$$

よって、面積は

$$4\times 2\sqrt{3}\times \frac{1}{2}=4\sqrt{3} cm^2$$

となります。

二等辺三角形の高さの求め方　まとめ

二等辺三角形の高さを求めるためには

まず、頂角からまっすぐな線を引きましょう！

すると、直角三角形を作ることができるので

そこから三平方の定理を使ったり

角度がわかる場合には比を取って

高さを求めてきます。

以上！

二等辺三角形の高さがわからないときに

面積を求める問題の解説でした。

図形問題において

三平方の定理ってすっごく活用しやすいから

しっかりと覚えておこうね！

ファイトだー(/・ω・)/