Σシグマの計算ってマジでややこしい!
途中の計算が複雑すぎて、解説を見てもよくわからん。
分数でくくるってなに!?
Σの計算では、途中で式を展開せず、
共通因数をくくっていくのが一般的です。
その辺りの手順がよくわからん…
という方が多いようなので、
途中式も含めて丁寧に解説していきますね!
今回の内容をサクッと理解したい方は、こちらの動画もどうぞ!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
覚えておきたいΣシグマの公式
Σの計算をするためには、次の公式を覚えておきましょう!
【Σシグマの公式】
$$\displaystyle \sum_{ k = 1 }^{ n } c=nc (c:定数)$$
$$\displaystyle \sum_{ k = 1 }^{ n } k=\frac{1}{2}n(n+1) $$
$$\displaystyle \sum_{ k = 1 }^{ n } k^2=\frac{1}{6}n(n+1)(2n+1) $$
$$\displaystyle \sum_{ k = 1 }^{ n } k^3=\left\{\frac{1}{2}n(n+1)\right\}^2 $$
また、Σシグマの計算では次のように変形することができます。
$$\begin{eqnarray}\displaystyle &&\sum_{ k = 1 }^{ n } (2k^2+3k-1)\\[5pt]&&=2\sum_{ k = 1 }^{ n } k^2+3\sum_{ k = 1 }^{ n } k-\sum_{ k = 1 }^{ n }1 \end{eqnarray}$$
それぞれの項ごとにわけて、\(k\)に関係のない係数はΣの前に出すことができます。
こうやって変形することでΣの公式が適用しやすくなりますね(^^)
Σシグマの計算方法!
では、いくつかの例題を見ながらΣシグマの計算方法について確認してみましょう。
公式を当てはめて分数でくくり出す
次の和を求めよ。
$$\sum_{ k = 1 }^{ n }( 2k^2-k+7)$$
まずはΣの性質を利用して、バラバラにわけておきましょう。
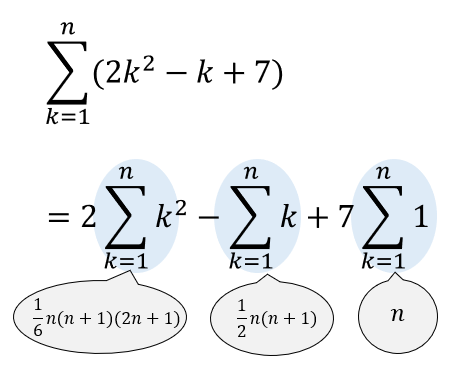
分けることができたら、そこへΣの公式をあてはめていきます。

Σの公式を当てはめたときに、約分してすべての項で分数が消える場合はラッキー。
ですが、分数が残ってしまう場合にはアンラッキー。
上のように通分して分母の数を揃えるようにしましょう。
式を展開してしまいたくなるのですが、
Σの計算では、展開をせず、因数分解を用いて答えを表していきます。
通分が完了したところで、共通因数をくくっていきます。
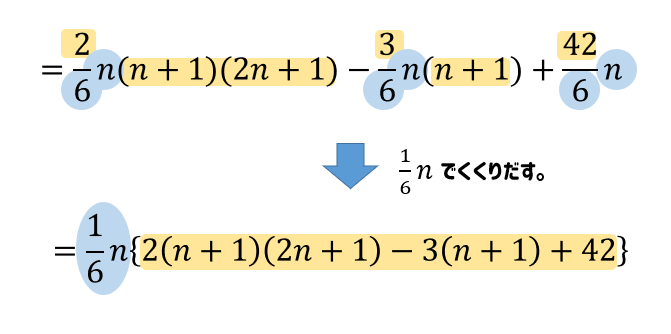
このとき、分数は共通因数としてくくり出され
かっこの中には残りません。
ここまできたら、あとはかっこの中身を展開してまとめていきましょう。

もうこれ以上、かっこの中身も因数分解できないので
これで計算完了となります。
通分して分母を揃える ⇒ 分数を含めて共通因数をくくり出す
ここの過程をクリアできれば、最後までたどり着けますね(^^)
nではなくて数の場合
次の和を求めよ。
$$\sum_{ k = 1 }^{ 10 }( 2k+1)$$
シグマ計算の終わりが\(n\) ではなく、数になっている場合。
これも先ほどと同じようにΣの公式を当てはめていけばOK。
ただし、公式の\(n\)であった部分を数に置き換えてください。

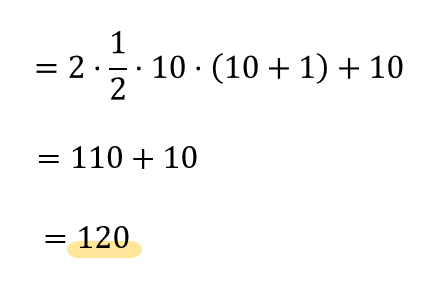
\(n\)ではなく、数になっている場合には
因数分解を気にすることなく、
計算を進めていけばいいので、ちょっとラクですね!
また、次のように
$$\sum_{ k = 7 }^{ 20 }( 2k+1)$$
始まりが1ではない場合。
Σシグマの公式は、始まりが1のときしか使えません。
なので、次のように工夫して考えてみるとよいです。
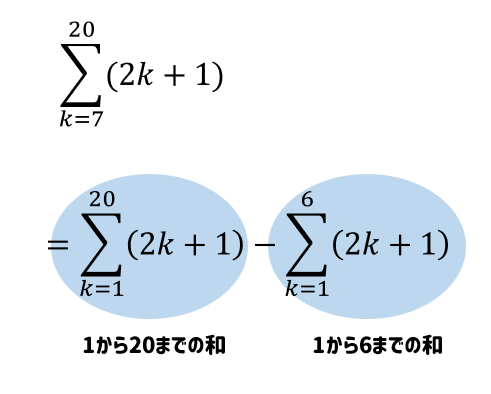
こうすれば、Σの公式を利用しながら解いていくことができますね!
等比数列の場合
次の和を求めよ。
$$\sum_{ k = 1 }^{ n }2^{k-1}$$
え、\(k\)乗がでてくる公式なんてあったっけ…!?
となってしまうのですが、\(k\)乗がでてくる式といえば等比数列です。
\(2^{k-1}\)は、初項1、公比2の等比数列ですね。
なので、この場合には等比数列の和の公式に当てはめて計算していけばOKです。

等比数列の和についてはこちらで詳しく解説しています。
まとめ!
お疲れ様でした。
Σの計算をするためには、まずは公式を覚えること!
そして、途中の計算では通分して分数をくくり出すというのもポイントでしたね。
何回も計算練習をして、
スラスラ解けるようにしておきましょう(/・ω・)/











わかりやすかったです✨
まとめの所に「お疲れさまでした!」って書いててくださり心が救われました
ありがとうございます!
シグマの計算は大変ですから
ほんとにお疲れ様でした^^
とってもわかりやすく参考になりました!
テスト前に確認できて助かりました