【苦手な人向け】絶対値の方程式、不等式の解き方をイチから解説！

高校数学Ⅰで学習する

「絶対値の方程式・不等式の解き方」

についてイチから解説していきます。

 

絶対値とは、原点からの距離のことでしたね。

このことを頭に入れておくことが大事です。

 

今回取り上げる問題は以下の通り。

それぞれの解き方をイチから確認していこう！

 

今回の記事は、こちらの動画でも解説しています！

絶対値の方程式・不等式（場合分けなし）

絶対値とは、原点からの距離のことでしたね。

こちらの問題を式ではなく、文章で考えてみましょう。

$$|x|=3$$

↓

\(x\)の絶対値は\(3\)

↓

\(x\)は原点からの距離が\(3\)である。

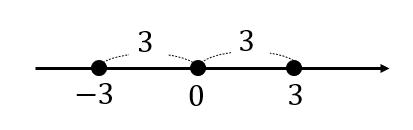
よって、\(\color{red}{x=\pm3}\) になる。

このように考えることができます。

 

つまり、絶対値の方程式では絶対値をとって右辺の数に±をつければOKということですね。

 

この不等式も先ほどと同じように文章で考えてみましょう。

$$|x|<3$$

↓

\(x\)の絶対値は\(3\)より小さい。

↓

\(x\)は原点からの距離が\(3\)より小さい。

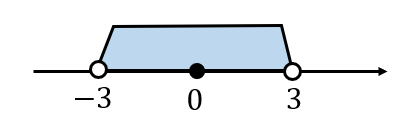
よって、\(\color{red}{-3<x<3}\) になる。

このように考えることができます。

絶対値が小さいということだから、原点寄りの場所、つまり内側の範囲ということになります。

 

つまり、絶対値の不等式（小さい）では絶対値の中身は右辺の数の±にはさまれる形になるということですね。

 

この不等式も先ほどと同じように文章で考えてみましょう。

$$|x|>3$$

↓

\(x\)の絶対値は\(3\)より大きい。

↓

\(x\)は原点からの距離が\(3\)より大きい。

よって、\(\color{red}{x<-3,3<x}\) になる。

このように考えることができます。

絶対値が大きいということだから、原点から離れたの場所、つまり外側の範囲ということになります。

 

つまり、絶対値の不等式（大きい）では絶対値の中身は右辺の数の±の外側の形になるということですね。

例題の解説

絶対値の方程式を、絶対値をなくして±をつける！

$$\begin{eqnarray}|2x+4|&=&6\\[5pt]2x+4&=&\pm 6\\[5pt]2x+4=6& / &2x+4=-6\\[5pt]2x=2 &/& 2x=-10\\[5pt]x&=&-5,1\cdots(解)\end{eqnarray}$$

 

絶対値が数より小さいときには、右辺の数の±にはさまれる形！

$$\begin{eqnarray}|x-2|&<&4\\[5pt]-4<x-2&<&4\\[5pt]-4+2<x&<&4+2\\[5pt]-2<x&<&6\cdots(解) \end{eqnarray}$$

 

絶対値が数より大きいときには、右辺の数の±より外側！

$$\begin{eqnarray}|2x+5|&≧&2\\[5pt]2x+5≦-2,2&≦&2x+5\\[5pt]2x≦-7,-3&≦&2x\\[5pt]x≦-\frac{7}{2},-\frac{3}{2}&≦&x\cdots(解) \end{eqnarray}$$

 

絶対値の方程式・不等式の解き方（場合分けあり）

絶対値の外に\(x\)があるときには場合分けが必要です。

場合分けのやり方は以下の通りです。

 例題の解説（方程式）

絶対値の外に\(x\)があるので場合分けが必要！

まずは絶対値の中身が0以上になる場合を考える。

このときは絶対値をそのままはずして解いていくことができます。

\(x-3≧0\) つまり、\(x≧3\)のとき

$$\begin{eqnarray}x-3&=&2x\\[5pt]-x&=&3\\[5pt]x&=&-3\end{eqnarray}$$

ここで求まった\(x=-3\)が場合分けの範囲\(x≧3\)の中に含まれているか確認します。

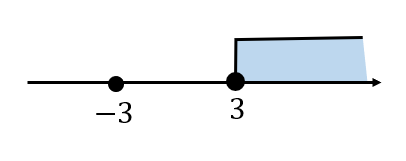
入ってないですね…ということで残念ながら\(x=-3\)は不適となります。

 

次は絶対値の中身が負になる場合を考えてみましょう。

このときは絶対値にマイナスをつけてはずします。

\(x-3<0\) つまり、\(x<3\)のとき

$$\begin{eqnarray}-(x-3)&=&2x\\[5pt]-x+3&=&2x\\[5pt]-3x&=&-3\\[5pt]x&=&1\end{eqnarray}$$

ここで求まった\(x=1\)が場合分けの範囲\(x<3\)の中に含まれているか確認します。

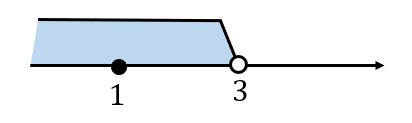
OK、入ってる！というわけで\(x=1\)が解となります。

$$x=1\cdots(解)$$

 

例題の解説（不等式）

こちらも絶対値の外に\(x\)があるので場合分けが必要です。

まずは絶対値の中身が0以上になる場合。

\(x-2≧0\)つまり、\(x≧2\)のとき

$$\begin{eqnarray}x-2&≧&2x-5\\[5pt]-x&≧&-3\\[5pt]x&≦&3 \end{eqnarray}$$

ここで求まった範囲と\(x≧2\)の共通範囲をとりましょう。

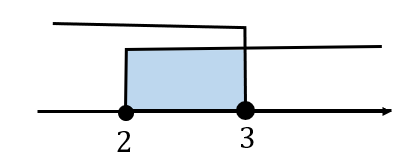
すると、\(2≦x≦3\)という範囲が求まります。

 

次は絶対値の中身が負になる場合を考えます。

このときはマイナスをつけて絶対値をはずします。

\(x-2<0\)つまり、\(x<2\)のとき

$$\begin{eqnarray}-x+2&≧&2x-5\\[5pt]-3x&≧&-7\\[5pt]x&≦&\frac{7}{3} \end{eqnarray}$$

ここで求まった範囲と\(x<2\)の共通範囲をとりましょう。

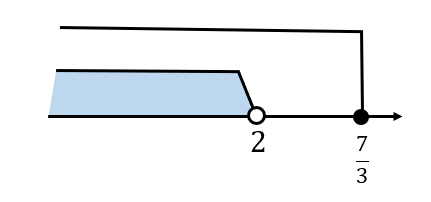
すると、\(x<2\)という範囲が求まります。

 

最後に、場合分けによって求めた2つの範囲をあわせます。

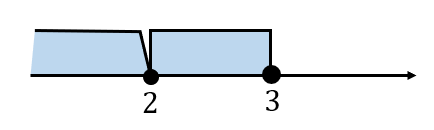
すると、解は

$$x≦3\cdots(解)$$

となります。

 

場合分けをすること。

場合分けの条件との共通範囲をとること。

最後は2つの範囲をあわせること。

これらがポイントとなりますね。

 

では、次の例題もサクッと解説しておきます。

\(x≧-1\)のとき

$$\begin{eqnarray}x+1&>&5x\\[5pt]-4x&>&-1\\[5pt]x<\frac{1}{4} \end{eqnarray}$$

\(x≧-1\)との共通範囲は、\(-1≦x<\frac{1}{4}\cdots①\)

\(x<-1\)のとき

$$\begin{eqnarray}-x-1&>&5x\\[5pt]-6x&>&1\\[5pt]x<-\frac{1}{6} \end{eqnarray}$$

\(x<-1\)との共通範囲は、\(x<-1\cdots②\)

①と②をあわせた範囲が解になるので

$$x<\frac{1}{4}\cdots(解)$$

 

絶対値が2つあるときの解き方

絶対値が2つ以上あるときには、それぞれを組み合わせた形で場合分けを考えていきます。

\(|x|\)の場合分けは、\(x≧0\)、\(x<0\)のとき

\(|x-3|\)の場合分けは、\(x≧3\)、\(x<3\)のときとなります。

これを組み合わせて考えるとこんな感じ。

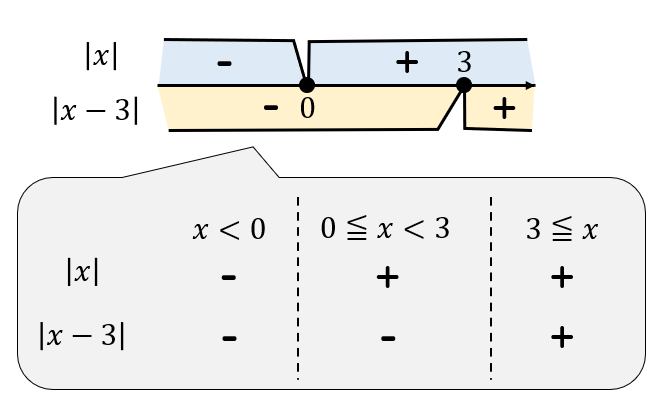
このような3つの組み合わせが考えられるってわかるね。

なので、上の範囲において場合分けをして解いていくようになります。

 

\(x<0\)のとき

$$\begin{eqnarray}-x-x+3&≦&5\\[5pt]-2x&≦&2\\[5pt]x&≧&-1 \end{eqnarray}$$

これと\(x<0\)の共通範囲は、\(-1≦x<0\cdots①\)

 

\(0≦x<3\)のとき

$$\begin{eqnarray}x-x+3&≦&5\\[5pt]3&≦&5\end{eqnarray}$$

つまり、\(0≦x<3\cdots②\)の範囲では全てOKということ。

 

\(3≦x\)のとき

$$\begin{eqnarray}x+x-3&≦&5\\[5pt]2x&≦&8\\[5pt]x&≦&4\end{eqnarray}$$

これと\(3≦x\)の共通範囲は、\(3≦x≦4\cdots③\)

 

最後に①②③の範囲をあわせると

$$-1≦x≦4\cdots(解)$$

 

まとめ！

絶対値の方程式、不等式では、まず絶対値の外に\(x\)があるかどうかを見ましょう。

絶対値の外に\(x\)がなければ場合分けは不要。

原点からの距離の位置関係から式を変形していけばOKです。

 

一方、絶対値の外に\(x\)がある場合には場合分けが必要。

絶対値の中身が0以上、負になるバターンで分けて考えていきましょう。

場合分けをしたときには、求まった値が範囲に含まれているかどうかなど、チェックする項目が多いのも注意ですね。

 

大事な問題なので、たくさん練習して解けるようにしておきましょう！