【中2数学】式の計算のやり方をイチから解説するぞ！

【参考記事】

＞文字の表し方を基礎から

＞文字式の計算をマスターしよう！

＞分数の計算をマスターしよう！

かっこの前が＋のときには、かっこの中身はそのままでしたね。

$$(3x+2y)=3x+2y$$

$$+(4x-y)=4x-y$$

なので、かっこをはずすと次のような式になります。

$$\begin{eqnarray}(3x+2y)+(4x-y)&=&3x+2y+4x-y \end{eqnarray}$$

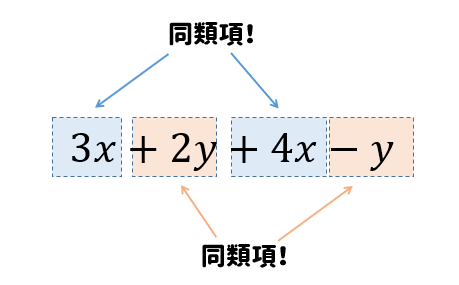
同類項とは、文字の部分が同じ項のことをいいます。

同類項をまとめると次のようになります。

$$\begin{eqnarray}&&(3x+2y)+(4x-y)\\[5pt]&=&3x+2y+4x-y\\[5pt]&=&3x+4x+2y-y\\[5pt]&=&7x+y \end{eqnarray}$$

同類項をまとめるってなんやねん！

って思った方もいるかもしれませんが、1年生で学習した文字式の加減と同じく文字の前についている数を足したり引いたりすればいいだけですね。

$$\large{7x+y}$$

同類項がまとまり、これ以上計算できるところがありません。

よって、これで完成！

かっこの前が－のときには、かっこの中身は符号がチェンジでしたね。

$$-(2x^2-3x)=-2x^2+3x$$

なので、かっこをはずすと次のような式になります。

$$\begin{eqnarray}(3x^2-x)-(2x^2-3x)&=&3x^2-x-2x^2+3x \end{eqnarray}$$

かっこの前がマイナスになっているときには、かっこをはずすときの符号でミスが起こりやすいです。

なので、手順①はミスしないように慎重にやってくださいね。

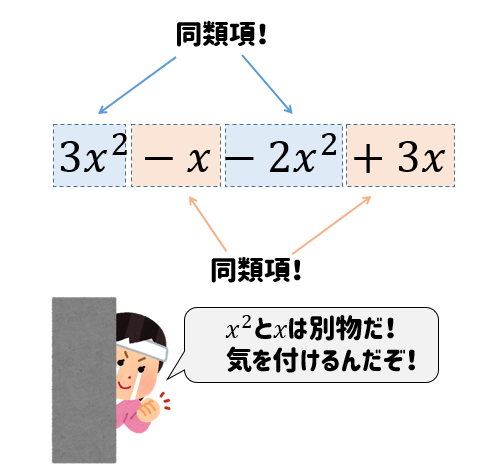
ここでの同類項は注意が必要！

同じ\(x\)という文字を使っていたとしても、\(x^2\)と\(x\)は別物として考えます。

なので、\(x^2\)と\(x\)を足したり、引いたりしてまとめることはできませんので気を付けてください。

同類項をまとめると次のようになります。

$$\begin{eqnarray}&&(3x^2-x)-(2x^2-3x)\\[5pt]&=&3x^2-x-2x^2+3x\\[5pt]&=&3x^2-2x^2-x+3x\\[5pt]&=&x^2+2x  \end{eqnarray}$$

$$\large{x^2+2x}$$

同類項がまとまり、これ以上計算できるところがありません。

よって、これで完成！

手順①　数どうし、文字どうしをかける

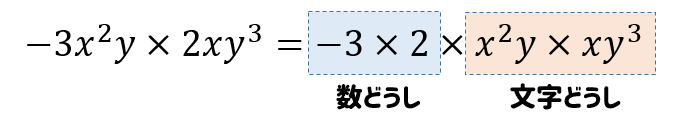
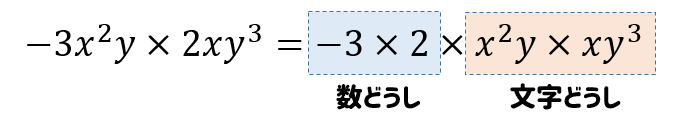
手順②　同じ文字は個数に応じて指数で表す

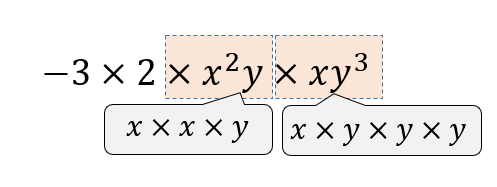
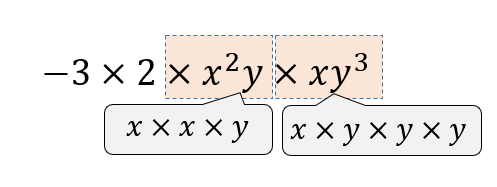
文字どうしの部分に注目すると、\(x\)は全部で3個、\(y\)は全部で4個あることが分かります。

よって、計算は次のようになります。

$$\begin{eqnarray}&&-3x^2y\times 2xy^3\\[5pt]&=&-3\times 2\times x^2y\times xy^3\\[5pt]&=&-6x^3y^4 \end{eqnarray}$$

手順③　完成！

$$\large{-6x^3y^4}$$

これ以上、まとめる部分がないので

これにて完成だ！！

手順①　割る数を逆数にしてかける

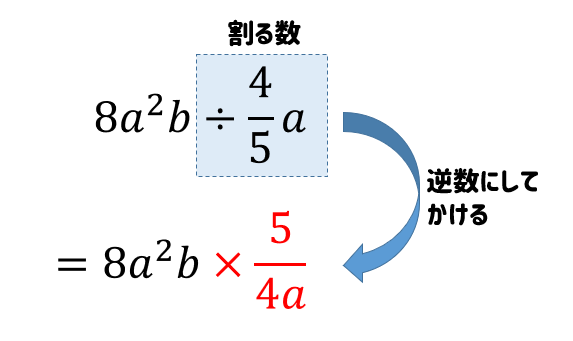
逆数にするとき、文字の位置に気を付けてくださいね。

$$\frac{4}{5}a=\frac{4a}{5}$$

このように、横についている文字は上にあるのと同じ。

逆数になると、\(\frac{5}{4a}\) のように下に文字がつくので間違えないようにしましょう！

手順②　数どうし、文字どうしを約分する

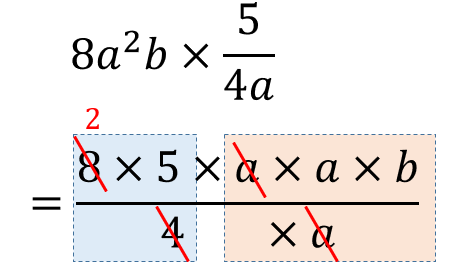
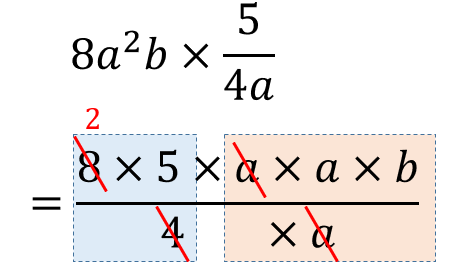
数字どうし、文字どうしを約分します。

文字の約分については初めてだと思いますが、とっても簡単！

同じ文字を消していけばよいだけですね(^^)

手順③　約分して残ったものどうしをかける

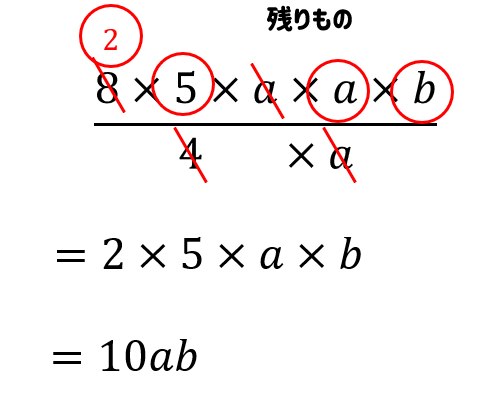
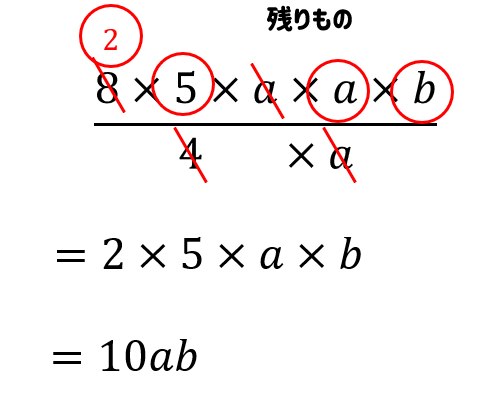
約分したあとの式って、線が入ったり数が上から書き込まれていたりと…

ちょっと見にくい(^^;)

なので、どれが残りものなのかハッキリさせるために〇印などをつけておくと良いですよ。

ここの手順はミスが起こりやすいので注意です！

手順④　完成！

$$\large{10ab}$$

これ以上、まとめる部分がないので

これにて完成だ！！