今回の記事では、数学Ⅱで学習する「点と直線の距離」を求める公式について解説していきます。
点と直線の距離を求める公式とは次のようなものです。
点と直線の距離を求める公式点\((x_1,y_1)\)と直線\(ax+by+c=0\)の距離
$$\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
んー、ややこしいね(^^;)
こんな公式覚えられねぇよ！！
っていう人も多いと思いますが、ここでは数学が苦手な方に向けてイチからやっていくので頑張ってついてきて欲しい！
ポイントは式を覚えるのではなく、形で覚えちゃおうって感じ(^^)
ってことで、やるぞ、やるぞ、やるぞー(/・ω・)/
Contents
点と直線の距離を求める公式を使ってみよう！
そもそも、点と直線の距離というのは
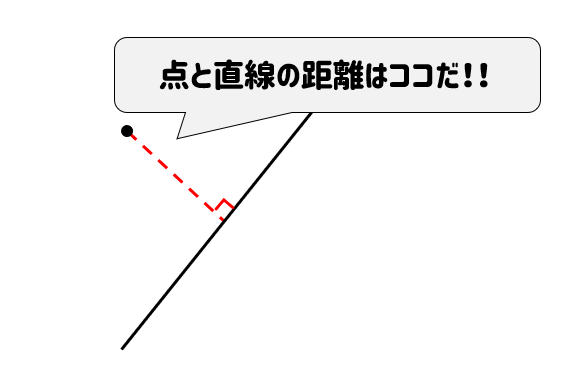
こういったところの長さのことだね。
点と直線を最短で結んだときにできる線分の長さのことだ！
これを公式を用いることで簡単に求めちゃいましょうっていうのが今回の学習の狙いです。
では、具体例を用いて距離を求めてみましょう。
【例題】
点\((1,2)\) と直線\(3x-4y=1\) の距離を求めなさい。
まずは、直線の式に注目！
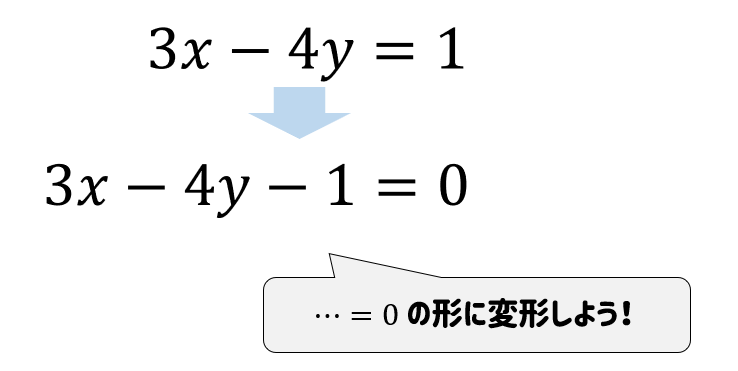
このように、直線の式を \(\cdots=0\) の形に変形できたら準備OKです。
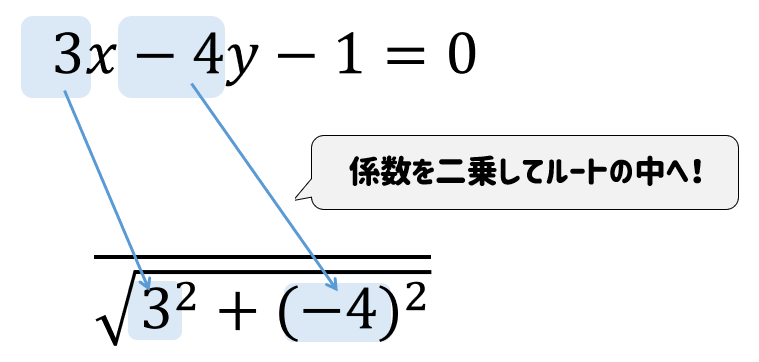
\(x\)と\(y\)についている数を二乗してルートの中に入れるべし！
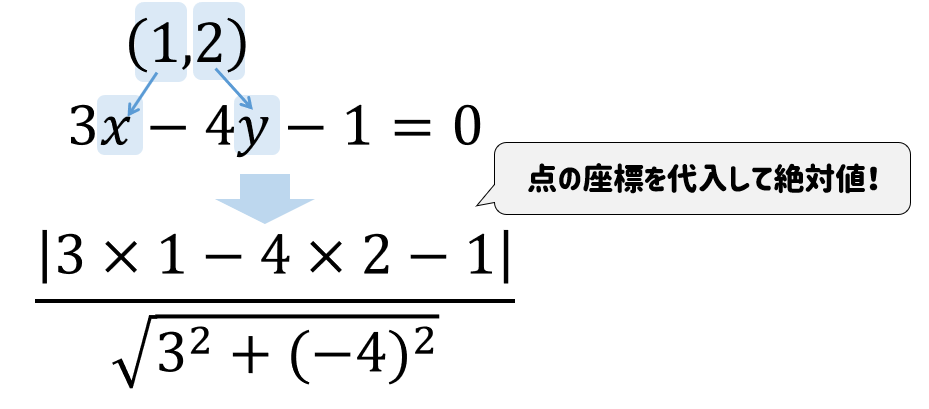
次に、点の座標を直線の式に代入して絶対値で囲むべし！
あとは計算して完了だ！
$$\begin{eqnarray}&&\frac{|3\times 1-4\times 2-1|}{\sqrt{3^2+(-4)^2}}\\[5pt]&=&\frac{|-6|}{\sqrt{25}}\\[5pt]&=&\color{red}{\frac{6}{5}} \end{eqnarray}$$
答え
$$\frac{6}{5}$$
簡単だね！
点と直線の距離を求める公式点\((x_1,y_1)\)と直線\(ax+by+c=0\)の距離
$$\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
こうやって公式で覚えようとすると、文字がたくさんで複雑…
ってなっちゃうので、点と直線の距離を求める場合
次のような手順として覚えちゃいましょう！
【点と直線の距離を求める手順】
- 直線の式を \(\cdots =0\) の形に変形したら準備OK
- \(x\)と \(y\) の係数を二乗してルートの中へ！
- 点の座標を直線の式に代入して絶対値！
- 計算すれば完了だ！
では、次の章では練習問題を用意しているので
たくさん練習して理解を深めていきましょう！
点と直線の距離を求める【練習問題】
点と直線の距離を求める公式まとめ！
お疲れ様でした！
しっかりと手順を覚えてしまえば、点と直線の距離を求めることなんて楽勝ですね(^^)
複雑な見た目の公式を頑張って覚えるのではなく、計算のやり方を覚えてしまえば良いのです。
見た目がややこしそうなモノこそ
中身はシンプルで易しかったりするものです。
それは人も同じですよねｗ
【点と直線の距離を求める手順】
- 直線の式を \(\cdots =0\) の形に変形したら準備OK
- \(x\)と \(y\) の係数を二乗してルートの中へ！
- 点の座標を直線の式に代入して絶対値！
- 計算すれば完了だ！
がんばっているのに60点の壁をクリアできない中3生の方へ
頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。
もしかして、
このような問題に直面していませんか？
- 模試になると点がガクッと落ちる
- 復習のやり方が分からない
- 勉強してもすぐに忘れる
- 凡ミスが直らない
- 家だと集中して勉強できない
- 問題集を買っても、1人で解けなくて途中でやめてしまう
- 友人が点を伸ばしていて焦る
- 頑張りたいから何をすればいいか教えて欲しい
僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。
すごく勉強したのに試験の結果が36点…
「どうすればいいか分からない…」
「点を上げれる自信がない…」
自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！
なんと、たった2ヶ月で
36点 ⇒ 72点
なんと、驚きの36点UPを達成！
何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。
この勉強法を活用した人は、
43点 ⇒ 69点
67点 ⇒ 94点
人生初の100点！
このように次々と良い結果を報告してくれています＾＾
Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。
そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。
こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！
もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ
コメントを残す