中学2年生で学習する「単項式」「多項式」
それぞれの意味って何だっけ?
となっている方に向けて解説記事を書いていきます。
まずは結論から述べておくと次のようになります。
単項式…数や文字の乗法だけでつくられている式
【例】
$$3x, -3x^2y, \frac{5}{2}$$
多項式…単項式の和の形で表された式
【例】
$$x^2-4x+1, 3a-b+2$$
今回の記事内容はこちらの動画でも解説しています(/・ω・)/
[スタセミ中2バナー]
単項式の意味とは
単項式…数や文字の乗法だけでつくられている式
【例】
$$3x, -3x^2y, \frac{5}{2}$$
単項式とは
$$-3\times x\times x\times y=-3xy^2$$
このように数や文字の乗法だけでつくられている式のことをいいます。
この説明で分かりにくい…という方は項の数に注目すると良いでしょう。
\(-3xy^2\) は項が1つだけ。
項が1つ(単)だから、単項式なんだ!
多項式の意味とは
多項式…単項式の和の形で表された式
【例】
$$x^2-4x+1, 3a-b+2$$
多項式とは
$$x^2-4x+1=x^2+(-4x)+1$$
このように単項式が和によってつながって表されて式のことをいいます。
これは、項がたくさん(多)つながっているよね。
項がたくさん(多)だから、多項式なんだ!
単項式と多項式の違い
上で説明してきたように
単項式は、数や文字の乗法だけで表される式。
多項式は、単項式の和で表される式。
のことをいいます。
太字、赤字にしている部分は大事なところです。
テストでも穴埋め問題として問われることがあるので、それぞれの特徴として覚えておきましょう。
見た目の違いは明らかですね(^^)
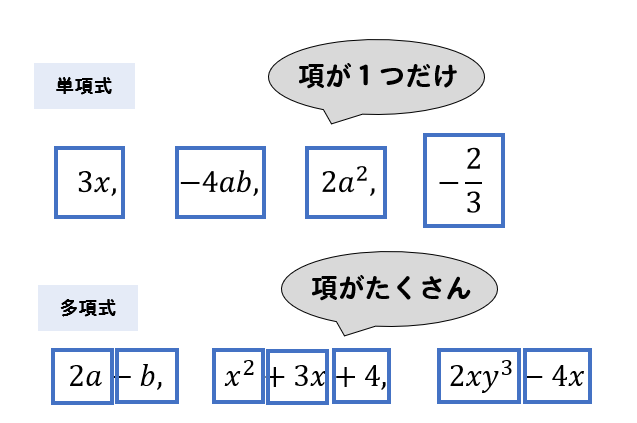
多項式の項を求める問題
多項式とは項がたくさんある式、と説明をしました。
では、どのような項がつながっているのか。
それぞれの項を求めなさいという問題を考えていきます。
次の多項式の項を答えなさい。
$$x^2-x+5$$
+、-の前で区切って考えましょう。
すると、どのような項があるのかがすぐにわかりますね!
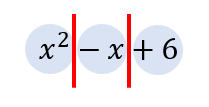
答え
$$x^2, -x, 6$$

まとめ!
お疲れ様でした!
単項式、多項式の意味について理解してもらえましたでしょうか?
式を見て判断できるだけでなく、それぞれの用語について言葉でも説明できるようにしておきましょう。
テストでは用語を説明させる問題も出題されます。
以下のポイント覚えておいて、得点アップを目指していきましょう(/・ω・)/
単項式は、数や文字の乗法だけで表される式。
多項式は、単項式の和で表される式。
今回の単元が含まれる定期テストでは、文字の計算がメインで出題されます。
計算ルール、練習問題についてはこちらの記事が参考になると思うので、続けて取り組んでみてくださいね!
















塾よりわかりやすくて助かったーーーーーー!!!!!!!!!!!
それはよかった!
他の記事も参考にしてみてくださいね^^
学校の先生の声はゴニョゴニョしてて聞き取れなくて意味がわからなかったけどこの記事がめちゃくちゃ分かりやすくて助かったーw
まじでわかりやすい