【中学数学】平行四辺形の証明問題を徹底解説！

今回は、中2で学習する証明問題の単元から

平行四辺形の証明問題について取り上げていくよ！

平行四辺形の証明問題とは、大きく分けて以下の2つだね

• 平行四辺形の性質を利用した合同の証明
• 平行四辺形になることを証明する

それでは、それぞれのパターンの問題について見ていこう！

今回の内容はこちらの動画でも解説しています＾＾

平行四辺形の性質を利用した合同の証明

まずは、平行四辺形の性質を利用しながら三角形の合同を証明していく問題を見ていきましょう。

ここでは、平行四辺形の性質をしっかりとおさえておく必要があります。

平行四辺形の性質

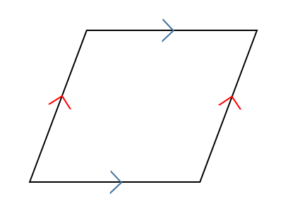
平行四辺形では、2組の対辺がそれぞれ平行。

平行であることを利用すると

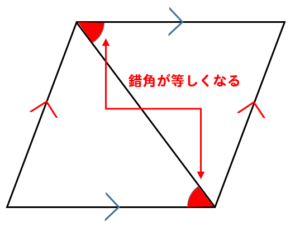
このように錯角が等しいということも分かります。

証明問題では、非常に重宝する性質です。

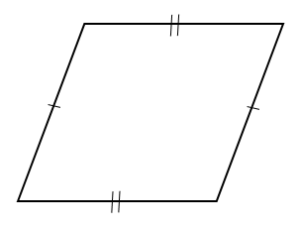
平行四辺形では、2組の対辺がそれぞれ等しい。

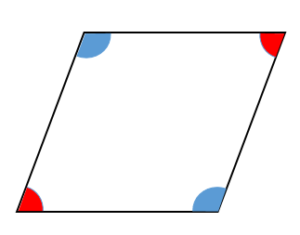
平行四辺形では、2組の対角がそれぞれ等しい。

平行四辺形では、対角線はそれぞれの中点で交わる。

問題に出てくる平行四辺形に対角線が引かれていれば、この性質を利用する可能性がぐっと高まりますね。

それでは、以上の性質を頭に入れた上で証明問題を見ていきましょう。

問題に挑戦！

下の図のように、平行四辺形ABCDの対角線の交点Oを通る直線が、DA、BCの延長と交わる点をそれぞれE、Fとするとき、EO＝FOとなる。このことを証明しなさい。

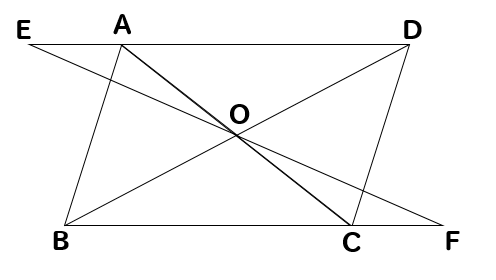
こちらでも書いていますが

＞＞＞【証明の書き方】合同な三角形の証明問題のかき方を基礎から解説！

いきなり証明を書こうとするのではなく

注目する三角形、等しくなる辺や角などを見つけることからスタートしていきましょう。

今回の問題では、EOとFOが等しくなることを証明したいので△EOAと△FOCに注目していけば良さそうだなということがわかります。

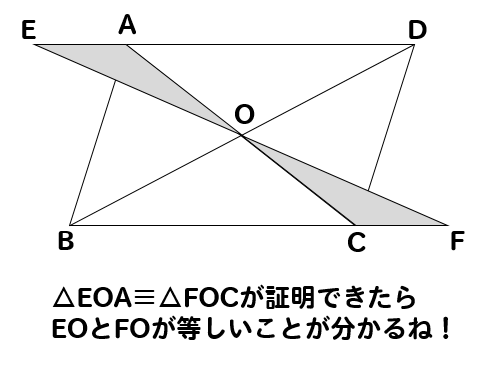
というわけで

△EOAと△FOCの三角形において、辺の長さや角の大きさが等しくなるところを見つけていきましょう。

まずは、平行四辺形の性質より

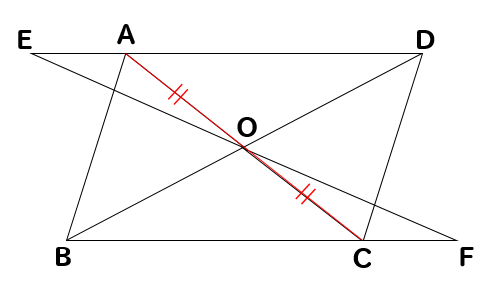
対角線がそれぞれの中点で交わるのでOA＝OCということが見つかりますね。

次は、対頂角！

辺が交差するところには対頂角アリです。

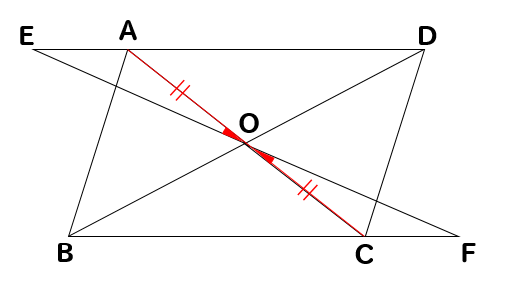
よって、∠EOA＝∠FOCということがわかります。

最後に、錯角！

平行四辺形の対辺は平行になるので、錯角が等しくなります。

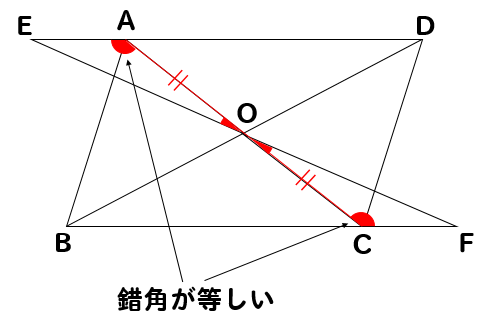
よって、∠EAO＝∠FCOとなります。

これで合同条件に必要な情報が揃いました。

1組の辺とその両端の角がそれぞれ等しいので

△EOA≡△FOCとなり

合同な図形の性質より、EO＝FOとなります。

それでは、これで証明の大まかな道筋が見えたので、ここから証明を書いていきます。

これで証明は完了です！

今まで解いてきた合同な三角形の証明をほとんど一緒ですね。

等しくなる辺や角を見つけるときに

平行四辺形の性質を利用していくだけなので

しっかりと性質を覚えておけば大丈夫です＾＾

記事の最後に演習問題を用意しているので

そこで理解を深めていきましょう！

平行四辺形になるための証明

次は、平行四辺形になるための証明を見ていきましょう。

こちらの問題は今までのものとは少し違います。

今までは、辺の長さや角の大きさが等しくなることを証明してきましたが、今回は注目する四角形が平行四辺形になるかどうかを証明していくというものです。

平行四辺形かどうかを調べるためには

これが言えたら平行四辺形だ！という

平行四辺形になるための条件というものがあります。

これを事前に知っておく必要があります。

平行四辺形になるための条件

平行四辺形になるための条件は以下の5つです。

平行四辺形だ！ということが証明できます。

ほとんどが平行四辺形の性質と同じなので覚えやすいのですが

『1組の対辺が平行でその長さが等しい』

というのだけは、ちょっと新しい感じなのでしっかりと覚えておきましょう。

しかも、この条件を使った証明がよく出題されるっていうね。

だから、絶対に覚えておいてね！

それでは、問題を見ていきましょう。

問題に挑戦！

下の図のように、平行四辺形ABCDの辺BC、AD上にそれぞれ点E、FをBE=DFとなるようにとるとき、四角形AECFは平行四辺形になる。このことを証明しなさい。

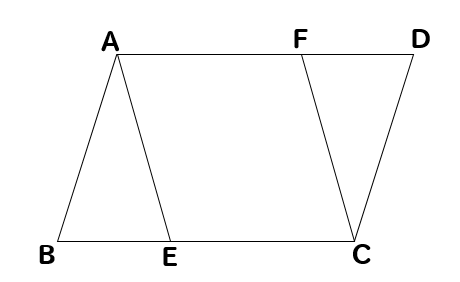
それでは、まず四角形AECFの辺の長さなどに注目していきましょう。

平行四辺形の性質から、対辺の長さは等しくなるのでAD=BCとなるよね。

そして、仮定からBE=DFと分かっているので

AF=ECということが分かります。

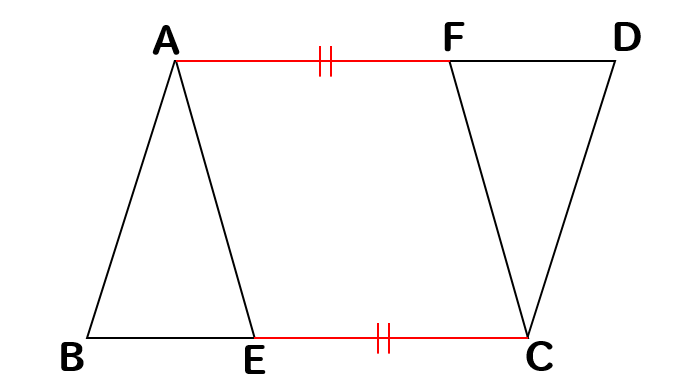
これはイメージが湧くかな？

長さが等しいモノから、同じ長さ分だけ取り除いたら

当然残っているモノどうしも長さは等しくなるよね。

数式で表すと

AF=AD-DF

EC＝BC－BE

AD=BC、DF＝BEだから

AFとECはそれぞれ表し方は違えど同じ値になるよね！

こんな感じです。

次は、平行四辺形の性質より対辺は平行になるのでAD//BC

辺の長さを短くしても当然、平行になるから

AF//ECということがわかります。

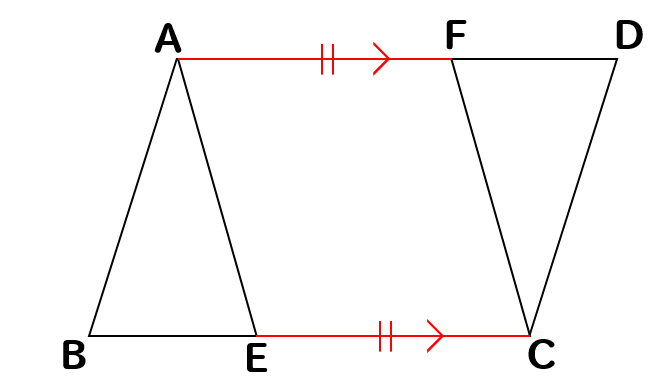
よって、1組の対辺が平行でその長さが等しいので

四角形AECFは平行四辺形であることが証明できます。

では、これを証明にしていきましょう。

このように、平行四辺形になることを証明する問題では

平行四辺形になるための条件を満たすかどうかを調べていけばOKです。

それでは、演習問題に挑戦して

平行四辺形の証明問題をマスターしていこう！

演習問題で理解を深める！

平行四辺形ABCDの頂点A、Cから対角線BDに垂線をひき、対角線との交点をそれぞれE、Fとする。このときAE=CFとなることを証明しなさい。

平行四辺形ABCDの対角線BD上に2点E、FをBE=DFとなるようにとる。このとき四角形AECFが平行四辺形であることを証明しなさい。

まとめ

お疲れ様でした！

平行四辺形の証明では、まずは性質を覚えることが大事！

そして、平行四辺形になることを証明するためには

これらの平行四辺形になるための条件を覚えておくことが必要です。

あとは、たくさんの問題に挑戦して

等しい辺や角を見つける練習をしていけば

証明問題は簡単に解けるようになります！

ファイトだー(/・ω・)/

直角三角形の証明問題に挑戦したい方はこちらもどうぞ＾＾

＞＞＞【直角三角形】証明問題の書き方とは？合同条件の使い方を徹底解説！