今回は高校生の方から
たくさんご質問いただく問題について解説しておきます。
それは…コレだ!
$$\Large{\sqrt{a^2}=|a|}$$
あ?
なんでルートをとったら、絶対値なんかついてんの!?
イミフなんだけど、マジで。

まぁまぁ…
言いたいことは分かりますが、ちょっとだけ話を聞いてくださいな。
√A2乗の計算についてはこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
ルートの中身が二乗⇒絶対値の理由
$$\Large{\sqrt{a^2}=|a|}$$
なぜルートがとれると絶対値がついてしまうのか。
$$\Large{\sqrt{a^2}=a}$$
これではダメなのでしょうか?
これはね
文字で考えていると難しく思えますが
具体的な数字で考えてみると簡単!
例えば
$$\Large{\sqrt{2^2}=2}$$
これはみなさん、簡単に理解できますよね。
ルートの中に二乗が出てきたから外に出す!みたいな。
じゃぁ、これだとどうでしょうか。
$$\Large{\sqrt{(-2)^2}=2}$$
ルートの中身は\((-2)^2\)になっていますが
外に出てきたのは2です。
↑そもそもコレがわかんねぇよ!
って方はこちらの記事で平方根の基礎について復習しておきましょう。
上のことから分かるように
ルートの中に二乗があれば、ルートの外に出せるが
外に出てくる数は、必ず正の数になっている!
ということがポイントなんですよね。
二乗だからって、そのまま外に出てくるわけではないのです。
『二乗になっていれば、正の数になって外に出てくる』
これは言い換えれば
『二乗になっていれば、その数の絶対値が外に出てくる』
という意味になります。
だから、厳密に式を書いてみると
$$\Large{\sqrt{2^2}=|2|=2}$$
$$\Large{\sqrt{(-2)^2}=|-2|=2}$$
このようになるわけです。
だから…
$$\Large{\sqrt{a^2}=|a|}$$
中身が二乗になったからといって
そのまま\(a\)を外に出したらダメというわけです。
次では、ルートを簡単にするのに
場合分けが必要な問題をやっておきましょう。
場合分けが必要な問題
次の式の根号をはずし、整式で表せ。
$$\sqrt{(x-2)^2}$$
これは先ほどやったように
ルートの中身が二乗になっていれば、絶対値をつけて外に出す。
ということを利用すれば…
$$\large{\sqrt{(x-2)^2}=|x-2|}$$
ここまで簡単にすることができます。
しかし、困ったことに…
絶対値の中身が0以上になるか、負になるか判断がつきません。
このままでは絶対値が外せませんね…
そのため
場合分けが必要になってくるわけです。
まず、絶対値の中身が0以上になる場合
\(x-2≧0\)より\(x≧2\)のとき
$$\large{\sqrt{(x-2)^2}=|x-2|=x-2}$$
次に、絶対値の中身が負になる場合
\(x-2<0\)より\(x<2\)のとき
$$\large{\sqrt{(x-2)^2}=|x-2|}$$
$$\large{=-(x-2)}$$
$$\large{=-x+2}$$
以上のことをまとめると答えは
\(x≧2\)のとき、\(x-2\)
\(x<2\)のとき、\(-x+2\)
となります。
今回の問題のように
絶対値をつけてルートを外したんだけど
絶対値の中身の符号が分からない!?
というときには場合分けが必要になります。
絶対値の中身が0以上のとき、負になるとき
この2つで場合分けをしていきましょう。
まとめ
お疲れ様でした!
高校数学になって、ちょっとつまずきそうになるのが
今回のような絶対値や場合分けの考え方ですね。
でも、じっくり話を聞いてみるとそんなに難しい事ではなかったりします。
見た目が難しそうに見えるだけっていうねw
今回、この記事にたどりついて
ここまで読んでいただけたということは
数学をなんとかできるようにしたい!
という強い意志をお持ちの方だと思います。
その調子でコツコツとやっていけば
必ずできるようになります。
必ず!!
だから、頑張っていきましょうね(^^)

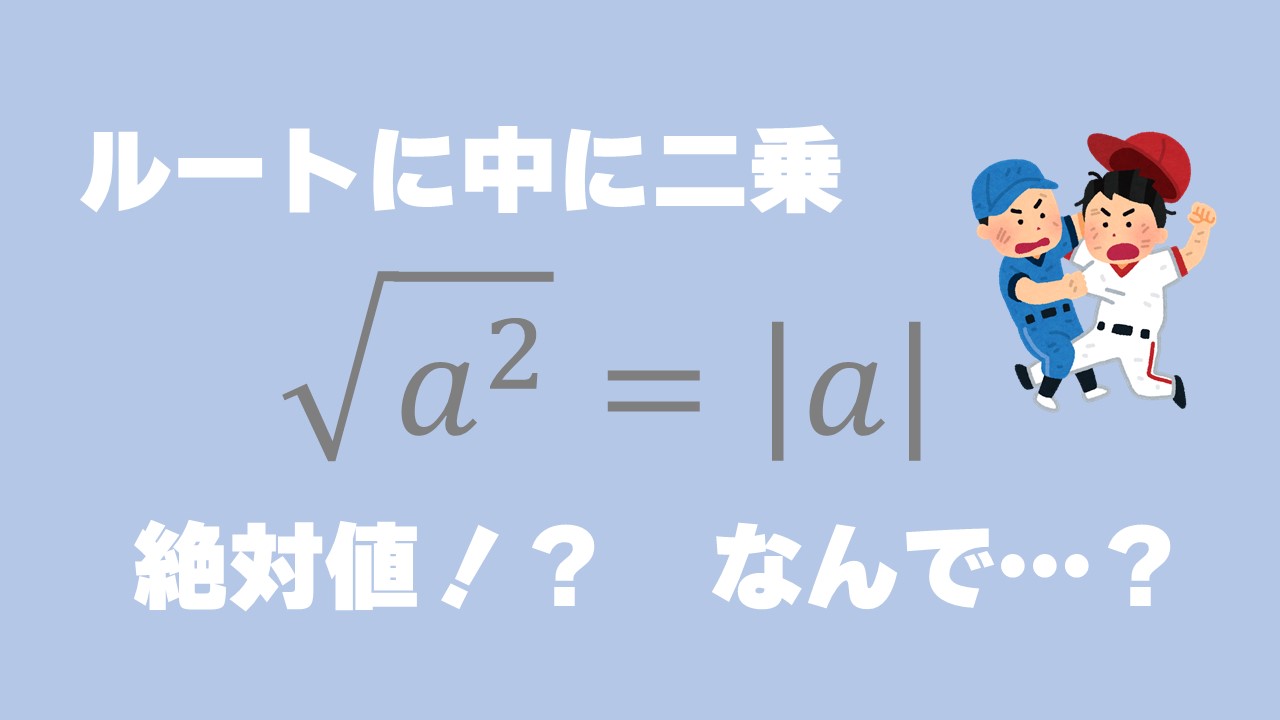
















コメントを残す