今回は、中1で学習する『一次方程式の文章問題』の中から
年齢を求める問題について解説していきます。
Aくんは13歳、Aくんのお父さんは43歳です。
お父さんの年齢がAくんの年齢の2倍になるのは何年後か。
また、そのときのAくん、お父さんの年齢はいくつになるか求めなさい。
今回の記事はこちらの動画でも解説しています(/・ω・)/
年齢を求める文章問題のポイント!
何年後に…というように年齢を考える問題では
\(x\)年後!
というように問題で与えられた条件を満たすまでに
何年かかるかを文字で置いてあげるのがポイントです。
当然ですが
Aくんもお父さんも同じように歳を重ねます。
1年後であれば2人の年齢は
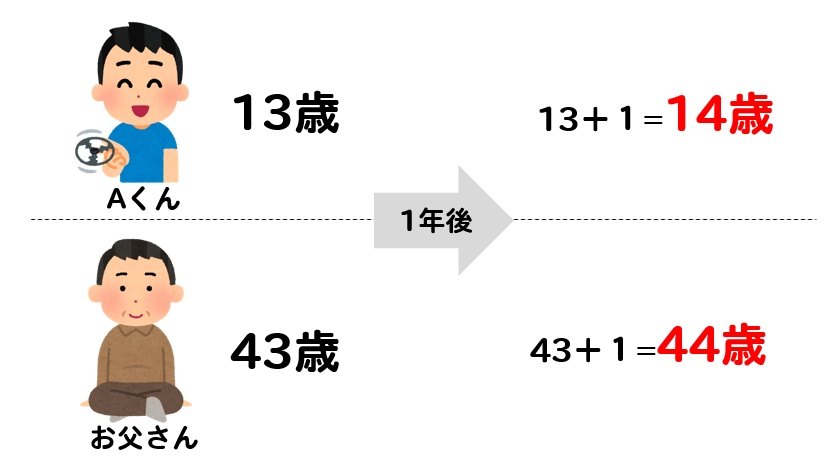
このように1歳ずつ歳を重ねます。
そして
\(x\)年後であれば
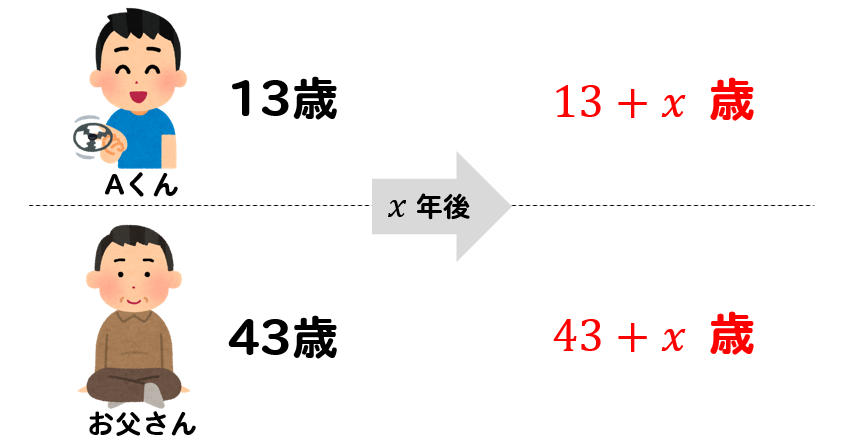
このように文字を使って年齢を表すことができます。
方程式を作るときには、このように文字を使って表した値を使っていきます。
年齢の文章問題を解くコツ
- \(x\)年後というように文字でおく
- 今の年齢\(+x\)という形で\(x\)年後の年齢を表す
年齢問題の解説!
Aくんは13歳、Aくんのお父さんは43歳です。
お父さんの年齢がAくんの年齢の2倍になるのは何年後か。
また、そのときのAくん、お父さんの年齢はいくつになるか求めなさい。
お父さんの年齢がAくんの年齢の2倍になるのが\(x\)年後だとすると
\(x\)年後の二人の年齢はそれぞれ
Aくん…\(13+x\)歳
お父さん…\(43+x\)歳
と表すことができます。
このとき、Aくんの年齢を2倍するとお父さんの年齢と等しくなるのだから
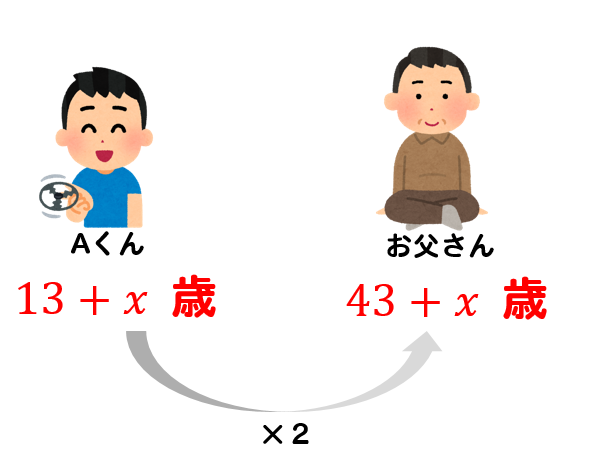
$$\large{2(13+x)=43+x}$$
このような方程式を完成させることができます。
方程式が完成したら、あとは解いていくだけですね(^^)
$$\large{2(13+x)=43+x}$$
$$\large{26+2x=43+x}$$
$$\large{2x-x=43-26}$$
$$\large{x=17}$$
よって、17年後にお父さんはAくんの2倍の年齢になることが分かりました。
17年後であるから、二人の年齢は
Aくん…13+17=30歳
お父さん…43+17=60歳
となります。
あぁ、たしかに2倍になっているな!
ってことがわかりますよね。
答え
17年後、Aくんは30歳でお父さんは60歳

練習問題で理解を深めよう!
それでは、練習問題に挑戦して理解を深めていきましょう。
子どもは3歳、父親は26歳です。
父親の年齢が子どもの2倍になるのは何年後か求めなさい。
次は少し方向性の違う問題を。
現在の父の年齢は、子どもの年齢の4倍であり、18年後に父の年齢は子どもの年齢の2倍になる。
現在の父と子どもの年齢を求めなさい。
まとめ
お疲れ様でした!
年齢を考える文章問題では
みな平等に歳を重ねる!
ということが大事です。
たくさん練習を重ねて理解を深めておきましょうね(/・ω・)/
他の文章題にも挑戦してみましょう。
















とても説明が分かりやすかったです。ありがとうございました。
ありがとうございます!!
とてもいい説明で分かりやすかったです。