今回は、小学生の算数で学習する
『つるかめ算』
について、基礎から学んでいこう。
つるかめ算とは、こんな感じの問題だったね!
鶴と亀が合わせて20匹います。足の数の合計は64本です。
鶴と亀はそれぞれ何匹ずついるでしょうか。
※問題文を長くするのが面倒だから、鶴を匹と数えさせてね(^^;
つるかめ算の解き方と考え方
つるかめ算を解くためには、中2で学習する連立方程式というものを使うと簡単に解くことができます。
しかし、小学生ではそういった計算方法は習っていない為
少し工夫しながら解いていく必要があります。
それでは、どのように解いていくのかというと
手順は次のようになります。
- 全部が〇〇だとしたら…
- 取り替えていく
それでは、上の問題をこの手順を使って解いていきましょう。
手順① 全部が〇〇だとしたら…
鶴と亀が合わせて20匹います。足の数の合計は64本です。
鶴と亀はそれぞれ何匹ずついるでしょうか。
鶴と亀を合わせたら20匹いる。
ということですが
全部がカメだったら…
という想定で問題を考えてみます。
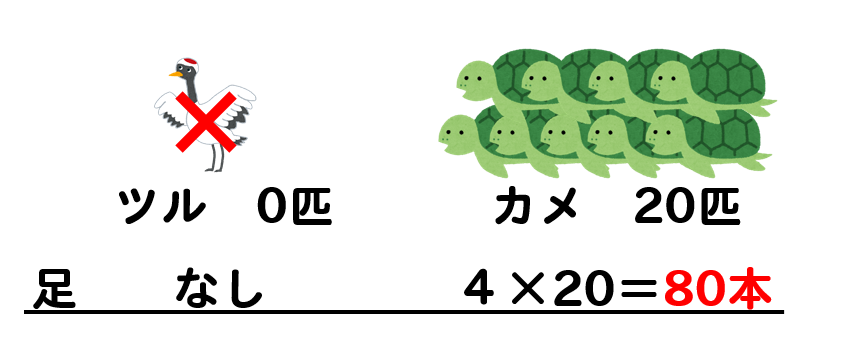
このように、全部がカメだとして考えると
足の合計数は80本となります。
問題では、足の合計が64本になるように。
ということですから
全部がカメだった場合には16本も足が多いということになります。
手順② 取り替えていく
全部がカメだとしたら64本を16本もオーバーしてしまうという結果になりました。
ここから、カメとツルを取り替えていきます。
カメを1匹減らして、ツルを1匹増やすと
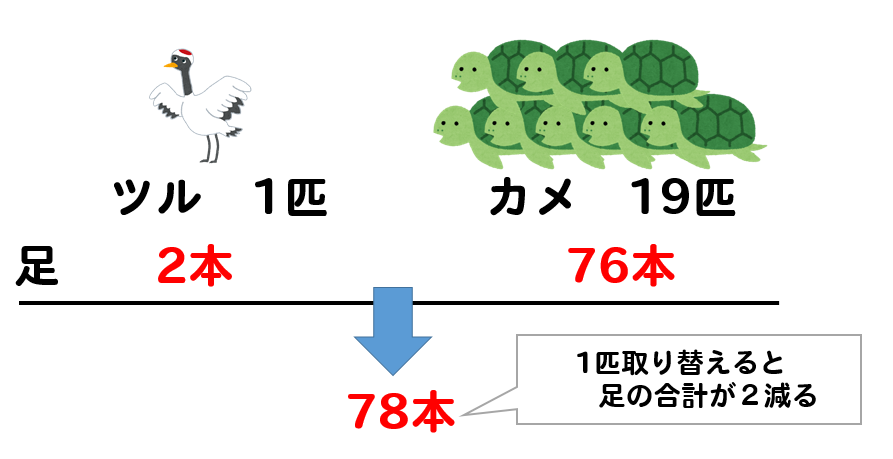
カメの足4本分が減り、ツルの足2本分が増えることになります。
よって、カメとツルを1匹取り替えると
足の合計数は\(4-2=2\)本分だけ減ることになります。
足の合計数を64本にするためには
16本分の足を減らす必要があるから
$$16\div2=8$$
つまり、8匹分だけ取り換えれば良いということになります。
よって、カメとツルを8匹分取り替えると…
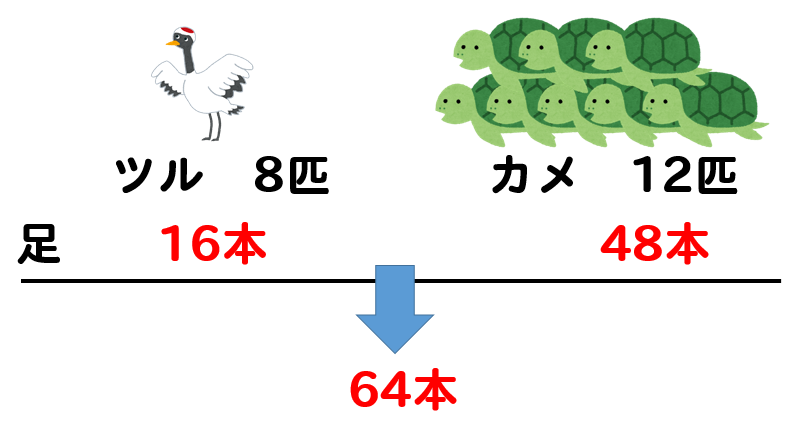
ツルが8匹、カメが12匹となり
問題で与えられた条件を満たしたことになりますね(^^)
つるかめ算では、このように
まずは全部が〇〇だったらということを考えます。
その次に、1匹ずつ取り換えを行って
問題の条件に合うようにしていきます。
うーん…
超簡単!!
という訳で、練習問題を通して理解を深めていきましょう。
つるかめ算 基本問題の練習!
50円切手と80円切手を合わせて10枚買うと、代金は620円でした。
それぞれの切手を何枚ずつ買ったのか求めなさい。
まとめ
お疲れ様でした!
つるかめ算って、やり方を知らない人にとっては難しい問題なんですよね…
特に、小学生のお子様に質問されて
どうやって教えていいのか分からないという親御さんが多いようです。
(連立方程式を使えば楽なのに…ぐぬぬ…)
この記事が、そういった方のお役に立っていれば幸いです(^^)
次の記事では、つるかめ算の応用編について解説していくよ!
中学受験を控えている方は
今回の基本問題をマスターして
次の応用編にも挑戦していきましょう。
















初めのところ「ずつ」が「ずる」になっていると思います!
とってもわかりやすく解説ありがとございます。
受験勉強にとっても役立ってます!
ご指摘ありがとうございました!
訂正しておきました^^
受験がんばってくださいね!
わかりやすかったです
それなです
解説が丁寧でわかりやすかったです。