今回は、平均算の問題を面積図というテクニックを用いて解く方法について解説していくよ！
面積図とは、かけ算を見た目で分かりやすく図で表したモノです。
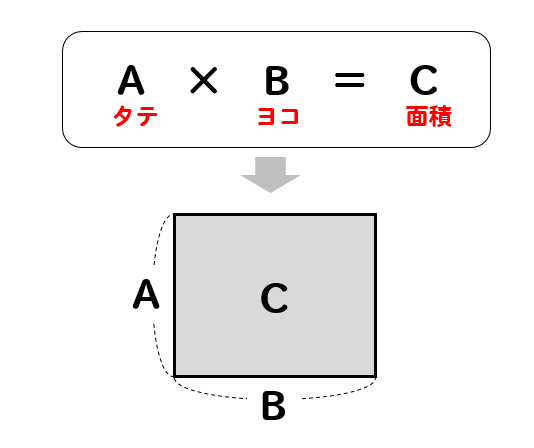
このように、掛け合わせる数を
それぞれタテ、ヨコの長さ
かけ算の答えを、面積として図形で表します。
平均算において、この面積図を用いると
こんな感じになりますね！
それでは、この面積図を用いて
どのように問題を解いていけば良いのか解説していきます(^^)
平均算の基本問題を確認しておきたい方はこちらもどうぞ！
面積図を用いて、平均算を解く方法！
まず、5回のテスト結果を面積図で表すとこんな感じ
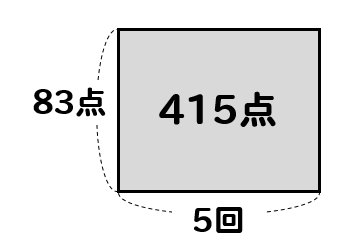
ここに6回目のテストが加わり、平均点が85点となるので
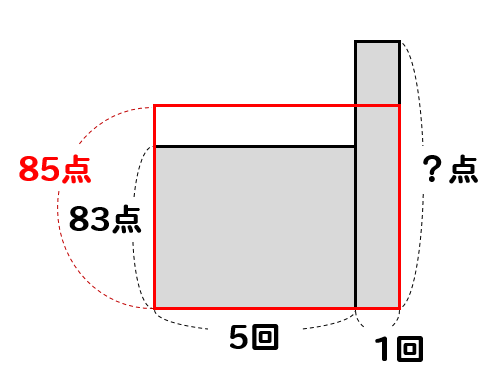
こんなイメージだね！
6回目のテストのはみ出している部分が
凹み部分を埋めて
ヨコ6回、タテ85点の面積を作り上げる感じだね
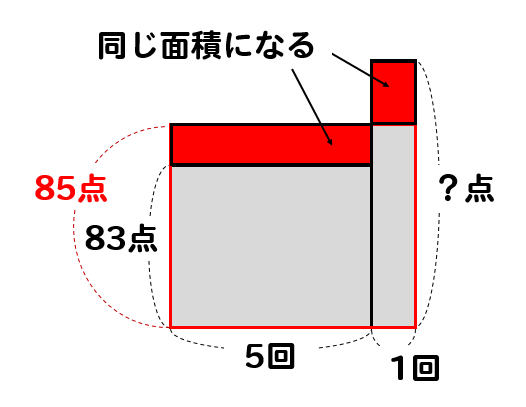
あとは、それぞれの長さや面積に着目していくと
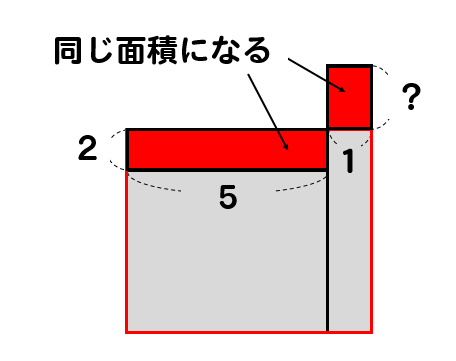
凹み部分の面積は\(2\times 5=10\)であるから
6回目のテストのはみ出している部分は
１０であることがわかります。
以上より、6回目のテストの点数は
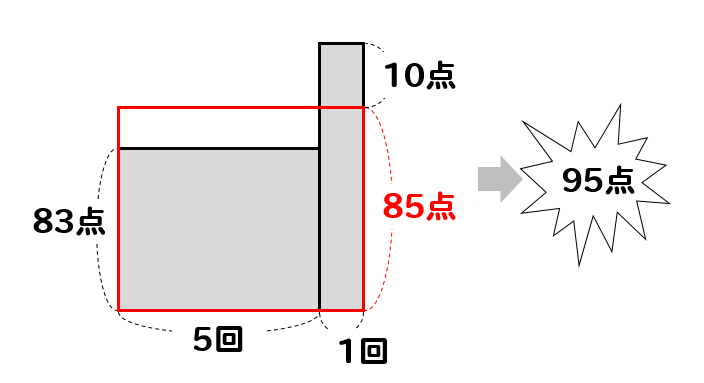
85点と10点を合わせて、95点となりました。
答え
95点
このように面積図を用いて
それぞれの辺の長さや面積に着目することで平均算の問題を解いてあげることができます。
面積図の利用とは、問題が応用になって
複雑になればなるほど効果を発揮してくれます。
というわけで、次は平均算の難問を
面積図を用いて、楽して答えを求めてみましょう。
平均算の難問を面積図で解いてみよう！
ややこしいね…(^^;
でも、面積図を使うと簡単になっちゃうよ！
図で表すとこんな感じ。
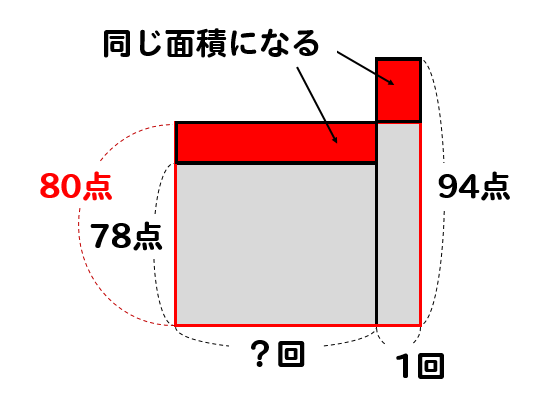
凹んだ部分とはみ出した部分に着目すると
？の部分の長さは7であることが分かります。
よって、今回のテストは8回目であることが求まりました！
面積図を用いると、簡単な面積を求める計算で答えがわかりましたね(^^)
答え
8回目
面積図に慣れるためにもう1問挑戦してみましょう。
これはちょっと難問かも…解けたらすごいぞ！
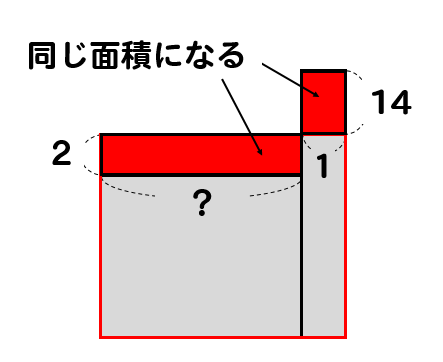
面積図で表すとこんな感じだね
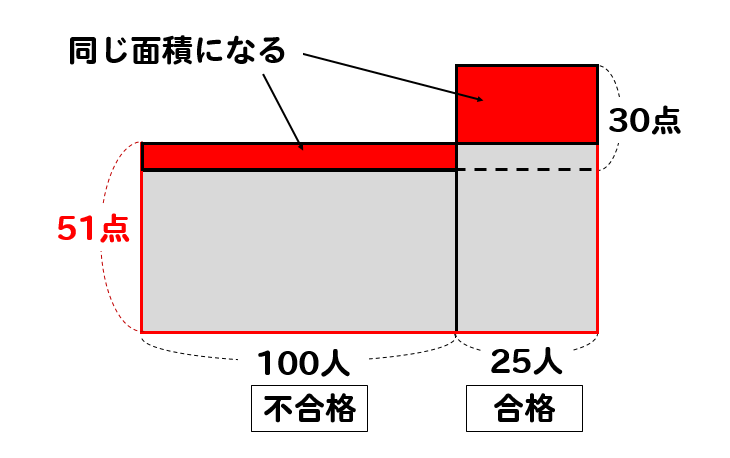
凹み部分とはみ出し部分を取り出して考えてみると
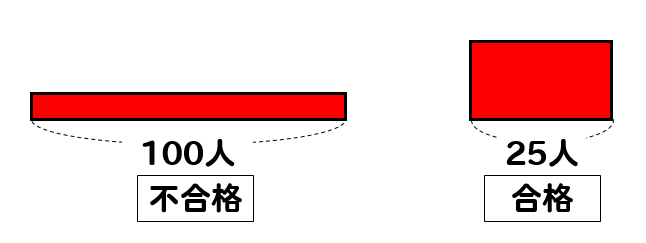
それぞれヨコの長さは
$$100:25=4:1$$
となっています。
すると、これらの図形の面積を等しくするためには
タテの比は、ヨコの比を逆にした\(1:4\)となります。
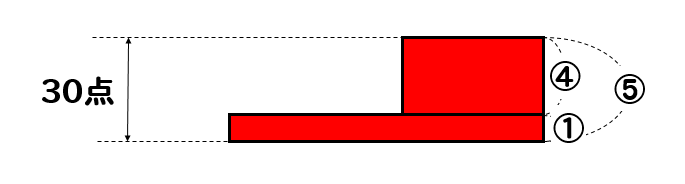
それぞれのタテの長さを合わせると、30点になるはずだから
凹み部分のタテの長さは
$$30\times \frac{1}{5}=6点$$
はみ出し部分のタテの長さは
$$30\times \frac{4}{5}=24点$$
よって、合格者の平均点は
$$51+24=75点$$
となります。
答え
75点
これは難しかったかな(^^;
比を使うことで、それぞれの長さを求めることができるぜ！っていう問題でした。
まとめ
お疲れ様でした！
面積図を用いることで
応用問題であっても、簡単に答えを求めることができましたね(^^)
こうやって見てみると
うぉぉぉ！
面積図最高！！
ってなるんだけど
面積図を使いこなすためには慣れが必要です。
初めのうちは、自力で図を書こうと思っても
なかなか正確に書けないものです。
習得してしまえば、こんなにも楽になるので
ぜひとも使いこなせるようになってもらいたい。
というわけで
練習あるのみだ！
ファイト(/・ω・)/
中学受験に必須な特殊算を学びたいなら
植木算、和差算、消去算、つるかめ算、過不足算、方陣算、旅人算、損益算、濃度算、日暦算、相当算、還元算、平均算、仕事算、倍数算、ニュートン算、流水算、通過算、時計算
中学受験を乗り切るためには、こんなにもたくさんの特殊算を身につけなければいけません。
しかも、学校学習の中では教えてくれないものばかり。
塾に通えない子供たちは独学で学習していかなければなりません。
これは正直、かなりキツイ…
だから、スタディサプリを使ってサクッと身につけてしまいましょう。
上で紹介した特殊算を１から丁寧に解説、そして演習問題で理解を深めることができます。
中学受験を乗り切るため、特殊算を身につけたいならスタディサプリが利用してみましょう！
コメントを残す