北海道の高校入試（数学）
2018年に出題された二次関数の問題に挑戦してみましょう！
【問題】
下の図のように，関数\(y=ax^2 \)（\(a\) は正の定数）…①のグラフ上に，2点A，Bがあります。点Aの\(x\)座標を\(-2\)，点Bの\(x\)座標を \(4\) とします。点Oは原点とします。次の問いに答えなさい。
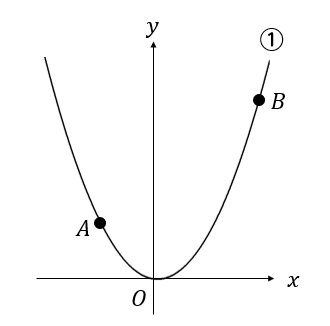
（1）\(a=2\) とします。①について，\(x\) の変域がのとき，\(y\) の変域を求めなさい。。
（2）2点A，Bを通る直線の傾きが \(1\)となるとき，\(a\) の値を求めなさい。
（3）\(a=1\) とします。点Bと \(y\)座標が等しい \(y\)軸上の点をCとします。①のグラフ上に点Pをとり，点Pの \(x\)座標を \(t\) とします。\(△BCP\) の面積 \(14\) となるとき，\(t\)の値を求めなさい。ただし，\(-2<t<4\) とします。
問題の解説！
問題の解説はこちらのPDFデータをご参考ください！
（1）（2）は小問でも出題される基本問題です。
関数においては，「変化の割合（傾き）」「変域」は超頻出！
必ず解けるように練習しておきましょう(/・ω・)/
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、以下の内容を無料でお届けします！
メルマガ講座の内容
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
コメントを残す